【机器学习笔记16】拉格朗日乘子法
【参考资料】
【1】《统计学习方法》
【2】《凸优化》
【3】小象学院 《凸优化》
凸集
直线和线段的表达
设 x 1 ≠ x 2 x_1 \ne x_2 x1̸=x2是 R n R^n Rn空间上的两个点,具有存在下列定义的点:
y = θ x 1 + ( 1 − θ ) x 2 y = \theta x_1 + (1 - \theta)x_2 y=θx1+(1−θ)x2组成一条过两点的直线,当 θ \theta θ取值在0、1之间表示一个线段。
另外一种表述方式: y = x 2 + ( x 2 − x 1 ) θ y = x_2 + (x_2 - x_1)\theta y=x2+(x2−x1)θ即 x 2 x_2 x2作为一个基点,直线表示为基点加上两点距离乘以一个参数形成偏移的点的集合。
仿射集合
仿射定义: 对于 x 1 , x 2 ∈ C θ ∈ R x_1, x_2 \in C \quad \theta \in R x1,x2∈Cθ∈R存在 θ x 1 + θ ( 1 − x 2 ) ∈ C \theta x_1 + \theta(1-x_2) \in C θx1+θ(1−x2)∈C
理解:这个集合对于线性变换具备封闭性
凸集
凸集定义:对于 x 1 , x 2 ∈ C θ ∈ [ 0 , 1 ] x_1, x_2 \in C \quad \theta \in [0,1] x1,x2∈Cθ∈[0,1]存在 θ x 1 + θ ( 1 − x 2 ) ∈ C \theta x_1 + \theta(1-x_2) \in C θx1+θ(1−x2)∈C
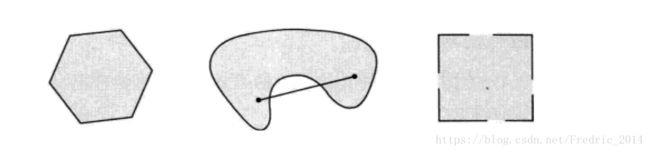
从简单几何图形上理解,即如下例
支撑超平面
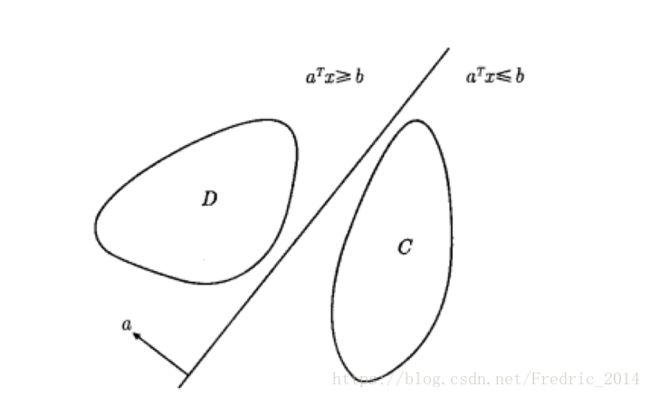
超平面 { x ∣ a T x = b } \{ x | a^Tx = b\} {x∣aTx=b}分离了两个不相交的凸集C和D,其中也称 a T x ≥ b a T x ≤ b a^Tx \ge b \quad a^Tx \le b aTx≥baTx≤b为超平面划分出来的两个半空间。
备注:当待分割的两个集合不是凸集,则未必存在一个超平面能够分割两个集合,那么这个时候如果取一个超平面能够是分割后损失最小(即尽可能的分割清楚),就是类似SVM这样的算法要完成的事情。
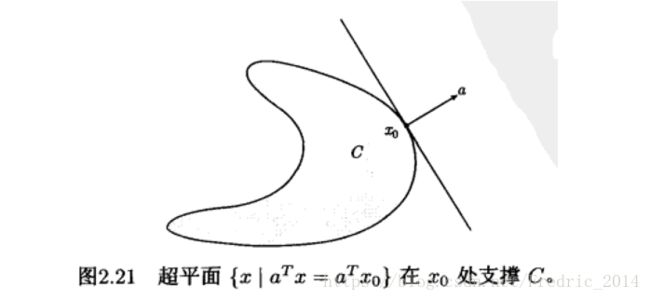
通过做垂直于两个凸集最短距离的超平面来作一个分割超平面,如下:

定义: a ≠ 0 a \ne 0 a̸=0 对于任何 x ∈ C x \in C x∈C满足 a T x ≤ a T x 0 a^Tx \le a^Tx_0 aTx≤aTx0,则称超平面 { x ∣ a T x = a T x 0 } \{ x | a^Tx=a^Tx_0\} {x∣aTx=aTx0}是集合C在 x 0 x_0 x0处的支撑超平面。
凸函数
凸函数定义
定义函数f: R n → R R^n \to R Rn→R是凸的,如果domf(定义域)是凸集,且对于任意 x y ∈ d o m f 0 ≤ θ ≤ 1 x \quad y \in domf \quad 0 \le \theta \le 1 xy∈domf0≤θ≤1有:
f ( θ x + ( 1 − θ y ) ) ≤ θ f ( x ) + ( 1 − θ ) f ( x ) f(\theta x + (1 - \theta y)) \le \theta f(x) + (1 - \theta)f(x) f(θx+(1−θy))≤θf(x)+(1−θ)f(x)

保凸运算
- 非负加权求和
严格的凸(凹)函数的非负加权求和也是凸(凹)函数
$ f = w_1f_1 + w_2f_2 + … + w_nf_n$
- 复合仿射映射
g ( x ) = f ( A x + b ) g(x) = f(Ax + b) g(x)=f(Ax+b)
若函数f是凸(凹)函数,则g也是凸(凹)函数
- 逐点最大或逐点上确界
若 f 1 f 2 f_1 \quad f_2 f1f2是凸函数,则 f = m a x ( f 1 , f 2 ) f = max(f_1, f_2) f=max(f1,f2)仍然是凸函数
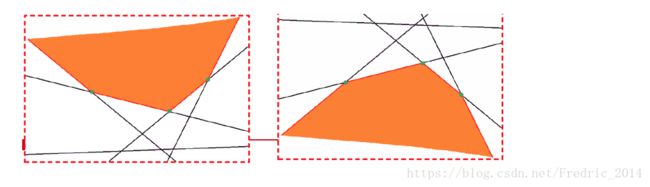
同时N条直线(凸函数)逐点求下确界是凹函数(必然有一个最大值,用在拉格朗日对偶中),如下图:
拉格朗日对偶
凸优化问题定义:
假设 f ( x ) c i ( x ) h j ( x ) f(x) \quad c_i(x) \quad h_j(x) f(x)ci(x)hj(x)是定义在 R n R^n Rn空间上的连续可微函数,考虑约束最优化问题:
求解: m i n x ∈ R n f ( x ) min_{x \in R^n}f(x) minx∈Rnf(x)
存在约束条件: c i ( x ) ≤ 0 , i = 1 , 2... k c_i(x) \le 0, i=1,2...k ci(x)≤0,i=1,2...k h j ( x ) = 0 , j = 1 , 2... l h_j(x)=0, j = 1,2...l hj(x)=0,j=1,2...l
引入拉格朗日函数:
L ( x , α , β ) = f ( x ) + ∑ i = 1 k λ i c i ( x ) + ∑ j = 1 l β j h j ( x ) L(x, \alpha, \beta)=f(x) + \sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x) L(x,α,β)=f(x)+∑i=1kλici(x)+∑j=1lβjhj(x) 其中$ \alpha_i \quad \beta_j$是拉格朗日乘子。
当我们固定x时,只考虑 λ \lambda λ,则拉格朗日函数可以看作是 λ \lambda λ作为直线的函数集,那么这些函数集的下确界构成一个凹函数,必然有极大值。
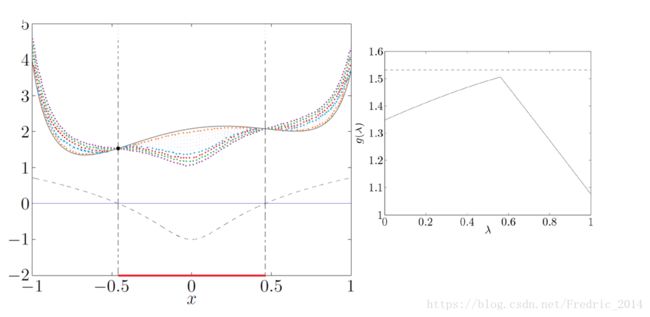
上图的备注:
- 上图针对最优化问题所构造的拉格朗日函数 L ( x , l a m b d a ) = f ( x ) + λ h ( x ) L(x,lambda)=f(x)+\lambda h(x) L(x,lambda)=f(x)+λh(x)
- 左图x轴红线部分代表x的取值范围,即最优化问题的约束
- 黑色实现代表原始函数f(x)
- 不同颜色的虚线,代表不同 λ \lambda λ下的 g ( λ ) = f ( x ) + λ h ( x ) g(\lambda)=f(x)+\lambda h(x) g(λ)=f(x)+λh(x)
- 左图对 m i n g ( λ ) min \quad g(\lambda) ming(λ)左图
- 可以得到结论,当我们对左图 m i n g ( λ ) min \quad g(\lambda) ming(λ)求最大值,也就得到了原始问题f(x)的最小值(重要)
拉格朗日对偶性:
这部分用于理解为什么拉格朗日对偶函数的最大值,能够对应到原始函数的最小值。
重新来看拉格朗日函数的定义
L ( x , α , β ) = f ( x ) + ∑ i = 1 k λ i c i ( x ) + ∑ j = 1 l β j h j ( x ) L(x, \alpha, \beta)=f(x) + \sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x) L(x,α,β)=f(x)+∑i=1kλici(x)+∑j=1lβjhj(x)
由于 c i ( x ) c_i(x) ci(x)是恒小于0的,因此整个 ∑ i = 1 k λ i c i ( x ) + ∑ j = 1 l β j h j ( x ) \sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x) ∑i=1kλici(x)+∑j=1lβjhj(x)的最大值是0。也就是说当 ∑ i = 1 k λ i c i ( x ) + ∑ j = 1 l β j h j ( x ) \sum_{i=1}^k\lambda_ic_i(x) + \sum_{j=1}^l\beta_jh_j(x) ∑i=1kλici(x)+∑j=1lβjhj(x)关于 λ \lambda λ的函数取最大值时,拉格朗日对偶函数等于原函数。
此时原始函数的求极小值问题等价于: m i n x m a x λ L ( x , λ , β ) min_x \quad max_{\lambda} \quad L(x, \lambda, \beta) minxmaxλL(x,λ,β)
最终我们将这个问题转换称对偶问题 m a x λ m i n x L ( x , λ , β ) max_{\lambda} \quad min_x \quad L(x, \lambda, \beta) maxλminxL(x,λ,β)`
我们有:
` m a x λ m i n x L ( x , λ , β ) ≤ m i n x m a x λ L ( x , λ , β ) max_{\lambda} \quad min_x \quad L(x, \lambda, \beta) \le min_x \quad max_{\lambda} \quad L(x, \lambda, \beta) maxλminxL(x,λ,β)≤minxmaxλL(x,λ,β)
备注:
对偶函数的最大值不一定等于原始函数的最小值,从上图的例子就可以看出,对偶函数的最大值略小于原始函数的最小值。若要两者相等,则需要满足KKT()条件。