GotoBlas2库

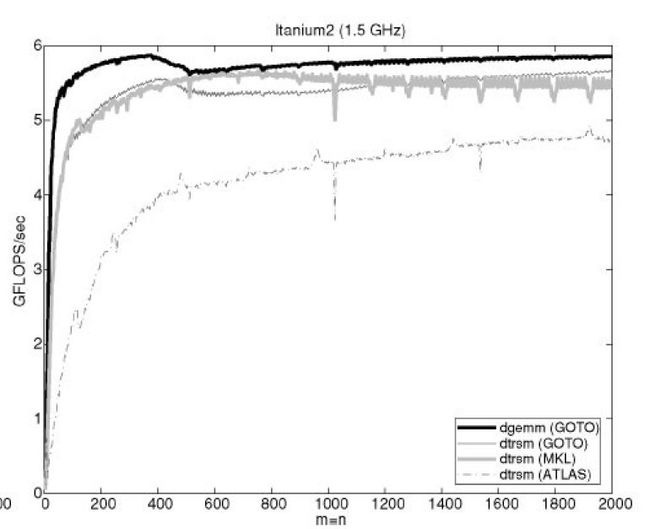
在High Performance Computing (HPC)领域，最有影响的矩阵库-GotoBLAS，在长久的等待后终于有了更新，而且是直接从1.26跳到了GotoBLAS2，似乎Goto重写了，目前可在官网上下载的最新版本是GotoBLAS2-1.13_bsd。

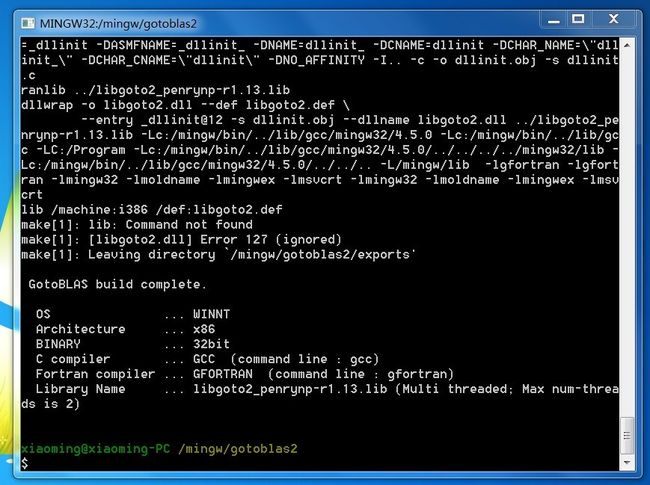
今天下载了，在mingw下近20分钟的编译过程后成功生成了libgoto2_penrynp-r1.13.lib库文件。

 

GotoBLAS2 has been released by the Texas Advanced Computing Center as open source software under the BSD license. This product is no longer under active development by TACC, but it is being made available to the community to use, study, and extend. GotoBLAS2 uses new algorithms and memory techniques for optimal performance of the BLAS routines. The changes in this final version target new architecture features in microprocessors and interprocessor communication techniques; also, NUMA controls enhance multi-threaded execution of BLAS routines on node. The library features optimal performance on the following platforms:

Intel Nehalem and Atom systems
VIA Nanoprocessor
AMD Shanghai and Istanbul

The library includes the following features:

• Configurations for a variety of hardware platforms
• Incorporation of features of many ISAs (Instruction Set Architecture)
• Implementation of NUMA controls to assure best process affinity and memory policy
• Dynamic detection of multiple architecture components, which can be included in a single binary (for binary distributions)

 

 

 

有机会研究一下源码。

 

 

What are the GotoBLAS?

The GotoBLAS codes are currently the fastest implementations of the Basic Linear Algebra Subroutines. Actually, GOTO is the developer's last name and does not mean "go to." (Nor is it pronounced "go to"; the correct pronunciation is "goh-toe.")

What is the main advantage of the GotoBLAS?

The advantage is fast calculation. Note that the actual performance depends in part on the code from which you call the GotoBLAS subroutine(s) and on the combination of architecture and operating system under which you are running. Your own tuning here can make a big difference.

Who develops and maintains the GotoBLAS?

Kazushige Goto was the sole developer of the GotoBLAS libraries. Originally, he targeted the Alpha chip architecture, but he later generalized the library to support various operating systems and architectures.

GotoBLAS is no longer under active development.

Which operating systems are supported?

Supported operating systems include:

Linux, FreeBSD, NetBSD, Solaris, OSX, AIX, Tru64, Unix , WindowsNT

Which architectures are supported?

Supported architectures include:

x86 family: Intel Pentium 3, Intel Pentium 4, Intel Core2, AMD Athlon, AMD Opteron

x86_64 family: Intel Pentium 4, Intel Core2, AMD Opteron

IA64 family: Intel Itanium2

Power family: IBM Power 4, Power 5, PPC970, PPC970MP, PPC440, PPC440 FP2

SPARC family: SPARC IV

Alpha family: EV4, EV5, EV6

How do I control the number of threads?

Currently, all of the GotoBLAS libraries are threaded and all attempt to use all of the processors available on your target computer. If you wish to control the number of threads, you need to specify the OMP_NUM_THREADS or GOTO_NUM_THREADS environment. Both of these environmental variables are identical except with respect to priority. The GOTO_NUM_THREADS environment is particularly useful for OpenMP users who want to control both the number of OpenMP tasks and the number of GotoBLAS threads.

 

好不容易编译了这库，当时因为把mingw32-make.exe改成了make.exe，出现有一堆错误，意识到这个之后，又改回mingw32-make.exe，这样会默认用msys中的make.exe来做，没有问题。

怎么用呢？我困惑了，头文件还要从源文件中复制出来，不像gmp来的那么轻松。我google关于gotoblas库的example 没有，百度更没有。

 

之后找到了一站点：

Appendix D GSL CBLAS Library

找到了一个例子：如下

D.4 Examples

The following program computes the product of two matrices using the Level-3 BLAS function SGEMM,

[ 0.11 0.12 0.13 ] [ 1011 1012 ] [ 367.76 368.12 ] [ 0.21 0.22 0.23 ] [ 1021 1022 ] = [ 674.06 674.72 ] [ 1031 1032 ]

The matrices are stored in row major order but could be stored in column major order if the first argument of the call to cblas_sgemm was changed to CblasColMajor.

#include #include int main (void) { int lda = 3; float A[] = { 0.11, 0.12, 0.13, 0.21, 0.22, 0.23 }; int ldb = 2; float B[] = { 1011, 1012, 1021, 1022, 1031, 1032 }; int ldc = 2; float C[] = { 0.00, 0.00, 0.00, 0.00 }; /* Compute C = A B */ cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, 2, 2, 3, 1.0, A, lda, B, ldb, 0.0, C, ldc); printf("[ %g, %g/n", C[0], C[1]); printf(" %g, %g ]/n", C[2], C[3]); return 0; }

To compile the program use the following command line,

gcc demo.c -lgslcblas

There is no need to link with the main library -lgsl in this case as the CBLAS library is an independent unit. Here is the output from the program,

$ ./a.out [ 367.76, 368.12 674.06, 674.72 ]

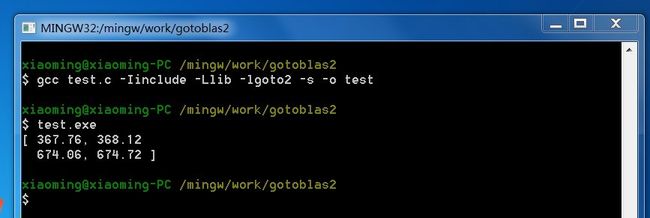
我想，GotoBlas2也能做，因为里面有cblas_sgemm这个函数。

折腾了好久，总算成功了！！！（最好把所有的头文件都复制到include文件夹中，lib中复制libgoto2_penrynp-r1.13.lib 改名为libgoto2.a）

-----------------------------------------------------------------------------

#include
#include     //gotoblas2中
#include            //gotoblas2中

 

int main (void)
{
  int lda = 3;

  float A[] = { 0.11, 0.12, 0.13,
                0.21, 0.22, 0.23 };

  int ldb = 2;
 
  float B[] = { 1011, 1012,
                1021, 1022,
                1031, 1032 };

  int ldc = 2;

  float C[] = { 0.00, 0.00,
                0.00, 0.00 };

  /* Compute C = A B */

  cblas_sgemm (CblasRowMajor,
               CblasNoTrans, CblasNoTrans, 2, 2, 3,
               1.0, A, lda, B, ldb, 0.0, C, ldc);

 

  printf("[ %g, %g/n", C[0], C[1]);
  printf("  %g, %g ]/n", C[2], C[3]);

  return 0; 
}

 

效果：

 

 

 

再来个复数矩阵乘法（简单的赋值了下值），会有一些警告信息：

#include #include //gotoblas2中 #include //gotoblas2中 typedef struct { float real; float imag; } CBLAS_TEST_COMPLEX; int main() { /*CBLAS_TEST_COMPLEX a[10*20], b[20*30], c[10*30]; CBLAS_TEST_COMPLEX alpha = {1.0, 0.0}; CBLAS_TEST_COMPLEX beta = {0.0, 0.0}; cblas_cgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, 10, 30, 20, &alpha, a, 20, b, 30, &beta, c, 30);*/ int i,j,k; CBLAS_TEST_COMPLEX a[2*2], b[2*3], c[2*3]; for(i=0;i<4;i++) { a[i].real=1.0; a[i].imag=2.0; } for(i=0;i<6;i++) { b[i].real=2.0; b[i].imag=3.0; } //初始化为0 for(i=0;i<6;i++) { c[i].real=0.0; c[i].imag=0.0; } CBLAS_TEST_COMPLEX alpha = {1.0, 0.0}; CBLAS_TEST_COMPLEX beta = {0.0, 0.0}; cblas_cgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, 2, 3, 2, &alpha, a, 2, b, 3, &beta, c, 3); printf("A[]=/n"); for(i=0;i<4;i++) printf("%.2f+(%.2fi)/n",a[0].real,a[0].imag); printf("B[]=/n"); for(i=0;i<6;i++) printf("%.2f +(%.2fi)/n",b[0].real,b[0].imag); printf("C=A*B/n"); for(i=0;i<6;i++) printf("%.2f +(%.2fi)/n",c[0].real,c[0].imag); system("Pause"); }

 

 结果为：

A[]=

1.00+(2.00i)

1.00+(2.00i)

1.00+(2.00i)

1.00+(2.00i)

B[]=

2.00+(3.00i)

2.00+(3.00i)

2.00+(3.00i)

2.00+(3.00i)

2.00+(3.00i)

2.00+(3.00i)

C=A*B

-8.00+(14.00i) 

-8.00+(14.00i)

-8.00+(14.00i)

-8.00+(14.00i)

-8.00+(14.00i)

-8.00+(14.00i)

接下来的事件很多了，并且容易了!!!!!!祝你好运!!!!!!!