线性模型篇之SVM数学公式推导
转载请注明出处:http://blog.csdn.net/gamer_gyt
博主微博:http://weibo.com/234654758
Github:https://github.com/thinkgamer
公众号:搜索与推荐Wiki
个人网站:http://thinkgamer.github.io
支持向量机(Support Vector Machine,SVM)是一个经典两类分类算法,其找到的分割超平面具有更好的鲁棒性,因此广泛使用在很多任务上,并表现出了很强优势。
介绍
给定一个两分类数据集D={(x^n, y^n)},n属于N,其中y_n 属于{+1,-1},如果两类样本是线性可分的,即存在一个超平面(公式-1)
w T x + b = 0 w^Tx + b =0 wTx+b=0
将两类样本分开,那么对于每个样本都有
y n ( w T x n + b ) > 0 y^n(w^Tx^n + b) > 0 yn(wTxn+b)>0
数据集D中的每个样本x^n 到分隔超平面的距离为:
γ n = ∥ w T x n + b ∥ ∥ w ∥ = y n ( w T x n + b ) ∥ w ∥ \gamma ^n = \frac{\left \| w^Tx^n +b \right \|}{ \left \| w \right \|} = \frac{y^n(w^Tx^n + b)}{ \left \| w \right \| } γn=∥w∥∥∥wTxn+b∥∥=∥w∥yn(wTxn+b)
我们定义整个数据集D中所有样本到分隔超平面的最短距离为间隔(Margin)(公式-2)
γ = m i n n γ n \gamma = \underset{n}{min} \gamma ^ n γ=nminγn
如果间隔 gamma越大,其分隔超平面对两个数据集的划分越稳定,不容易受噪声等因素影响,支持向量机的目的是找到一个超平面(w^* , b^ *)使得gamma最大,即(公式-3)
m a x w , b γ s . t . y n ( w T x n + b ) ∥ w ∥ ≥ γ , ∀ n \underset{w,b}{max} \qquad \gamma \\ s.t. \qquad \frac{y^n (w^Tx^n + b)}{\left \| w \right \|} \geq \gamma,\forall_n w,bmaxγs.t.∥w∥yn(wTxn+b)≥γ,∀n
令
∥ w ∥ . γ = 1 \left \| w \right \| . \gamma =1 ∥w∥.γ=1
则(公式-3)等价于(公式-4)
m a x w , b 1 ∥ w ∥ 2 s . t . y n ( w T x n + b ) ≥ 1 , ∀ n \underset{w,b}{max} \qquad \frac{1}{ \left \| w \right \| ^2} \\ s.t. \qquad y^n(w^Tx^n + b) \geq 1, \forall_n w,bmax∥w∥21s.t.yn(wTxn+b)≥1,∀n
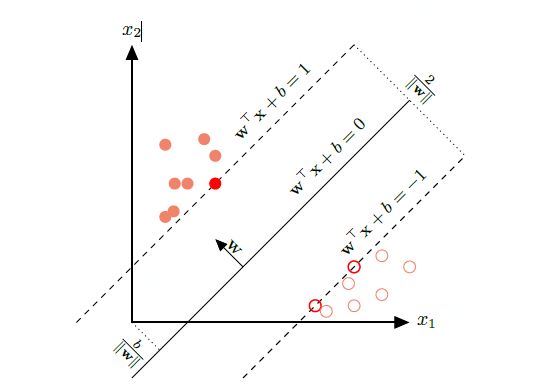
数据集中所有满足 y^n (w^T x^n +b) =1 的样本点,都称为支持向量(support vertor)
对于一个线性可分数据集,其分隔的超平面有多个,但是间隔最大的超平面是唯一的。下图给定了支持最大间隔分隔超平面的示例,其红色样本点为支持向量。
参数学习
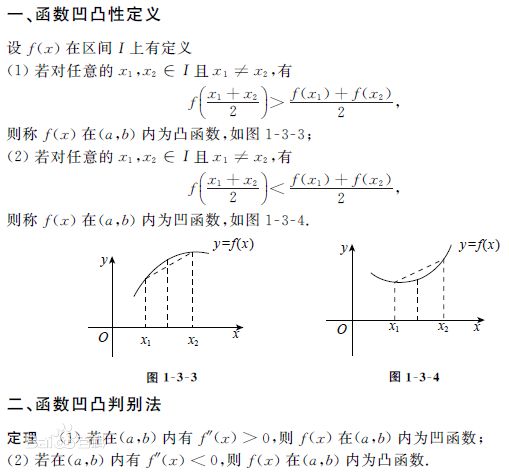
凸函数 & 凹函数
关于凹凸函数的定义和性质可以参考下图:
为了找到最大间隔分割超平面,将公式-4改写为凸优化问题(公式-5):
m i n w , b 1 2 ∥ w ∥ 2 s . t . 1 − y n ( w T x n + b ) ≤ 0 , ∀ n \underset{w,b}{min} \qquad \frac{1}{ 2} {\left \| w \right \| ^2} \\ s.t. \qquad 1-y^n(w^Tx^n + b) \leq 0, \forall n w,bmin21∥w∥2s.t.1−yn(wTxn+b)≤0,∀n
使用拉格朗日乘数法,公式-5的拉格朗日函数为(公式-6):
Λ ( w , b , λ ) = 1 2 ∥ w 2 ∥ + ∑ n − 1 N λ n ( 1 − y n ( w T x n + b ) ) \Lambda (w,b,\lambda )=\frac{1}{2} \left \| w^2 \right \| + \sum_{n-1}^{N} \lambda _n( 1-y^n(w^Tx^n + b) ) Λ(w,b,λ)=21∥∥w2∥∥+n−1∑Nλn(1−yn(wTxn+b))
其中
λ 1 ≥ 0 , . . . , λ N ≥ 0 \lambda _1 \geq 0,...,\lambda _N \geq 0 λ1≥0,...,λN≥0
为拉格朗日乘数。计算公式-6关于w和b的导数,并令其等于0得到(公式-7)
w = ∑ n = 1 N λ n y n x n w = \sum_{n=1}^{ N }\lambda _n y^nx^n w=n=1∑Nλnynxn
和(公式-8)
0 = ∑ n = 1 N λ n y n 0 = \sum_{n=1}^{N} \lambda _n y^n 0=n=1∑Nλnyn
将公式-7代入公式-6,并利用公式-8,得到拉格朗日对偶函数(公式-9):
Γ ( λ ) = − 1 2 ∑ n = 1 N ∑ m = 1 N λ n λ m y m y n ( x m ) T x n + ∑ n = 1 N λ n \Gamma(\lambda) = -\frac{1}{2} \sum_{n=1}^{N}\sum_{m=1}^{N} \lambda_n \lambda_m y^m y^n (x^m)^Tx^n + \sum_{n=1}^{N}\lambda_n Γ(λ)=−21n=1∑Nm=1∑Nλnλmymyn(xm)Txn+n=1∑Nλn
支持向量机的主优化问题为凸优化问题,满足强对偶性,即主优化问题可以通过最大化对偶函数
m a x λ ≥ 0 Γ ( λ ) max_{\lambda \geq 0} \Gamma(\lambda) maxλ≥0Γ(λ)
对偶函数 Gamma(lambda)是一个凹函数,因此最大化对偶数是一个凸优化问题,可以通过多种凸优化方法进行求解,得到拉格朗日乘数的最优值 lambda^* 。但由于其约束条件的数量为训练样本数量,一般的优化方法代价比较高,因此在实践中通常采样比较高效的优化方法,比如SMO(Sequential Minimal Optimization)算法等。
根据KKT条件中的互补松弛条件,最优解满足(公式-10)
λ n ∗ ( 1 − y n ( w ∗ T x n + b ∗ ) ) = 0 \lambda_n ^*(1-y^n(w^{*T}x^n+b^*))=0 λn∗(1−yn(w∗Txn+b∗))=0
如果样本x^n 不在约束边界上,(lambda_n)*,其约束失效;如果样本xn在约束边界上,(lambda_n)^* >=0。这些在约束边界上的样本点称为支持向量(support vector),即离决策平面距离最近的点。
再计算出 lambda*后,根据公式-7计算出最优权重w*,最优偏置b^可以通过任选一个支持向量(x,y)计算得到(公式-11)
b ∗ = y ~ − w ∗ T x ~ b^* = \tilde{y} - w^{*T}\tilde{x} b∗=y~−w∗Tx~
最优参数的支持向量机的决策函数为(公式-12)
f ( x ) = s g n ( w ∗ T x + b ∗ ) = s g n ( ∑ n = 1 N λ n ∗ y n ( x n ) T x + b ∗ ) f(x)=sgn(w^{*T}x+b^*)=sgn(\sum_{n=1}^{N} \lambda_n^* y^n(x^n)^Tx + b^* ) f(x)=sgn(w∗Tx+b∗)=sgn(n=1∑Nλn∗yn(xn)Tx+b∗)
支持向量机的决策函数只依赖 lambda_n^>0的样本点,即支持向量。
支持向量机的目标函数可以通过SMO等优化方法得到全局最优解,因此比其他分类器的学习效率更高。此外,支持向量机的决策函数只依赖与支持向量。与训练样本总数无关,分类速度比较快。
核函数
支持向量机还有一个重要的优点是可以使用核函数(kernal)隐式的将样本从原始特征空间映射到更高维的空间,并解决原始特征空间中的线性不可分问题。比如在一个变换后的特征空间中,支持向量机的决策函数为(公式-13)
f ( x ) = s g n ( w ∗ T ϕ ( x ) + b ∗ ) = s g n ( ∑ n = 1 N λ n ∗ y n K ( x n , x ) + b ∗ ) f(x)=sgn(w^{*T} \phi(x)+b^*)=sgn(\sum_{n=1}^{N} \lambda_n^* y^n K(x^n,x) + b^* ) f(x)=sgn(w∗Tϕ(x)+b∗)=sgn(n=1∑Nλn∗ynK(xn,x)+b∗)
其中
K ( x , z ) = ϕ ( x ) T ϕ ( z ) K(x,z)=\phi(x)^T \phi(z) K(x,z)=ϕ(x)Tϕ(z)
为核函数,通常不需要显式的给出φ(x)的具体形式,可以通过核技巧(kernel trick)来构造。比如以x,z属于R^2为例,我们可以构造一个核函数(公式-14)
K ( x , z ) = ( 1 + x T z ) 2 = ϕ ( x ) T ϕ ( z ) K(x,z)=(1+x^Tz)^2=\phi(x)^T\phi(z) K(x,z)=(1+xTz)2=ϕ(x)Tϕ(z)
来隐式的计算x,z在特征空间φ中的内积,其中:
ϕ ( x ) = [ 1 , 2 x 1 , 2 x 2 , 2 x 1 x 2 , x 1 2 , x 2 2 ] T \phi(x)=[1,\sqrt{2}x_1,\sqrt{2}x_2,\sqrt{2}x_1x_2,x_1^2,x_2^2]^T ϕ(x)=[1,2x1,2x2,2x1x2,x12,x22]T
软间隔
在支持向量机的优化问题中,约束条件比较严格。如果训练集中的样本在特征空间中不是线性可分的,就无法找到最优解。为了能够容忍部分不满足约束的样本,我们可以引入松弛变量,将优化问题变为(公式-15):
m i n w , b 1 2 ∥ w ∥ 2 + C ∑ n = 1 N ξ n s . t . 1 − y n ( w T x n + b ) − ξ n ≤ 0 , ∀ n ξ n ≥ 0 , ∀ n \underset{w,b}{min} \qquad \frac{1}{ 2} {\left \| w \right \| ^2} + C \sum_{n=1}^{N}\xi _n \\ s.t. \qquad 1-y^n(w^Tx^n + b) -\xi _n \leq 0, \forall n \\ \xi _n \geq 0, \forall n w,bmin21∥w∥2+Cn=1∑Nξns.t.1−yn(wTxn+b)−ξn≤0,∀nξn≥0,∀n
其中参数C>0用来控制间隔和松弛变量惩罚的平衡,引入松弛变量的间隔称为软间隔(soft margin)。公式-15也可以表示为经验风险+正则化项的形式(公式-16)。
m i n w , b ∑ n = 1 N m a x ( 0 , 1 − y n ( w T x n + b ) ) + 1 C . 1 2 ∥ w ∥ 2 \underset{w,b}{min} \qquad \sum_{n=1}^{N}max(0,1-y^n(w^Tx^n + b)) + \frac{1}{C}.\frac{1}{2}\left \| w \right \|^2 w,bminn=1∑Nmax(0,1−yn(wTxn+b))+C1.21∥w∥2
其中
m a x ( 0 , 1 − y n ( w T x n + b ) ) max(0,1-y^n(w^Tx^n + b)) max(0,1−yn(wTxn+b))
称为hinge损失函数,1/C可以看作是正则化系数。软间隔支持向量机的参数学习和原始支持向量机类似,其最终决策函数也只和支持向量有关,即满足
1 − y n ( w T x n + b ) − ξ n = 0 1-y^n(w^Tx^n + b) - \xi_n = 0 1−yn(wTxn+b)−ξn=0
的样本。