基于协同的ALS算法原理介绍与实现
转载请注明出处:http://blog.csdn.net/gamer_gyt
博主微博:http://weibo.com/234654758
Github:https://github.com/thinkgamer
公众号:搜索与推荐Wiki
个人网站:http://thinkgamer.github.io
ALS也是一种协同算法,其全称是交替最小二乘法(Alternating Least Squares),由于简单高效,已被广泛应用在推荐场景中,目前已经被集成到Spark MLlib和ML库中,在下一篇文章会对其使用方式进行详细介绍,本篇文章主要介绍ALS的底层算法原理。
最小二乘法(Least Squares)
在介绍ALS算法之前,先来了解LS,即最小二乘法。LS算法是ALS的基础,是一种数学优化技术,也是一种常用的机器学习算法,他通过最小化误差平方和寻找数据的最佳匹配,利用最小二乘法寻找最优的未知数据,保证求的数据与已知的数据误差最小。
LS也被用于拟合曲线,比如所熟悉的线性模型。下面以简单的线性一元线性回归模型说明最小二乘法。
假设我们有一组数据{(x1,y1),(x2,y2),(x3,y3)…}其符合线性回归,假设其符合的函数为如下:
y = w 0 + w 1 x y = w_0 + w_1 x y=w0+w1x
我们使用一个平方差函数来表达参数的好坏,平方差函数如下:
L n = ( y n − f ( x ; w 0 , w 1 ) ) 2 L_n = (y_n - f(x;w_0,w_1))^2 Ln=(yn−f(x;w0,w1))2
其中f(.) 表示我们假设的线性回归函数。显然Ln越小越好,Ln越小表示误差越小。假设有N个样本,则N个样本的平均平方差为:
L = 1 N ∑ n = 1 N ( y n − f ( x ; w 0 , w 1 ) ) 2 L = \frac{1}{N} \sum_{n=1}^{N} (y_n - f(x;w_0,w_1))^2 L=N1n=1∑N(yn−f(x;w0,w1))2
L越小表示参数w越精确,而这里最关键的就是寻找到最合适的w0和w1,则此时的数学表达式为:
a r g m i n w 0 , w 1 1 N ∑ n = 1 N ( y n − f ( x ; w 0 , w 1 ) ) 2 \underset{w_0,w_1}{arg \ min} \frac{1}{N} \sum_{n=1}^{N} (y_n - f(x;w_0,w_1))^2 w0,w1arg minN1n=1∑N(yn−f(x;w0,w1))2
将先行回归函数代入到最小二乘损失函数中,得到的结果为:
L = 1 N ∑ n = 1 N ( y n − w 0 − w 1 x n ) 2 1 N ∑ n = 1 N ( w 1 2 x n 2 + 2 w 1 x n ( w 0 − y n ) + w 0 2 − 2 w 0 y n + y n 2 ) L = \frac{1}{N} \sum_{n=1}^{N} (y_n - w_0 - w_1 x_n)^2 \\ \frac{1}{N} \sum_{n=1}^{N} (w_1 ^2x_n^2 + 2w_1x_n(w_0 - y_n) + w_0^2 - 2w_0y_n + y_n^2) L=N1n=1∑N(yn−w0−w1xn)2N1n=1∑N(w12xn2+2w1xn(w0−yn)+w02−2w0yn+yn2)
L函数取得最小值时,w0和w1的一阶偏导数一定是0(因为误差平方和是一个大于等于0的数,是没有最大值的,所以取得最小值时,一阶偏导数一定为0)。因为对L函数分别求偏导,使其等于0,并对w0和w1求解,即可。
交替最小二乘法(Alternating Least Squares)
ALS算法本质上是基于物品的协同,近年来,基于模型的推荐算法ALS(交替最小二乘)在Netflix成功应用并取得显著效果提升,ALS使用机器学习算法建立用户和物品间的相互作用模型,进而去预测新项。
基本原理
用户对物品的打分行为可以用一个矩阵(R)来表示:
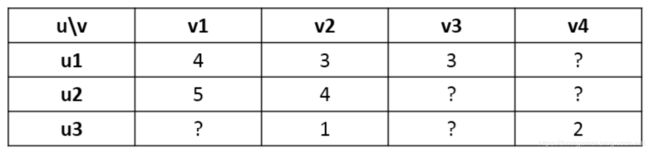
矩阵中的打分值 r_ij表示用户 u_i 对物品 v_j 的打分,其中”?”表示用户没有打分,这也就是要通过机器学习的方法去预测这个打分值,从而达到推荐的目的。
模型抽象
根绝协同过滤的思想,R矩阵的行向量对应每个用户U,列向量对应每个物品V。ALS的核心思想是:将用户和物品都投射到k维空间,也就是说假设有k个隐向量特征,至于这个k个隐向量是什么不用关系(可能是标签,年龄,性别等),将每个用户和每个物品都用k维的向量来表示,把他们的内积近似为打分值,这样便可以得到近似的评分。
R ≈ U V T R \approx UV^T R≈UVT
其中:
- R为打分矩阵(m*n,m表示用户个数,n表示物品个数)
- U表示用户对隐含特征的偏好矩阵(m*k)
- V表示物品对隐含特征的归属矩阵(n*K)
上述模型的参数就是U和V,求得U和V之后,就可以近似的得到用户对未评分物品的评分。
代价函数
求上述公式中的U和V,就需要一个代价函数来衡量参数的拟合程度。用户对物品的行为分为显式行为和隐式行为,两种不同类型的行为下,对应的代价函数也是不一样的。
关于显式行为和隐式行为的介绍可以餐考 我的《推荐系统开发实战》一书。
显式反馈代价函数
如果用户对物品有明确的评分行为,那么可以对比重构出来的评分矩阵和实际的评分矩阵,便可得到误差。由于用户对物品的评分却失很多,仅以有评分行为的物品去计算误差。下面是显式反馈的代价函数。
J ( U , V ) = ∑ i m ∑ j n [ ( r i j − u i v j T ) 2 + λ ( ∣ ∣ u i ∣ ∣ 2 + ∣ ∣ v j ∣ ∣ 2 ) ] J(U,V) = \sum_{i}^{m} \sum_{j}^{n}[(r_{ij} - u_iv_j^T) ^2 + \lambda ( ||u_i||^2 + ||v_j||^2 ) ] J(U,V)=i∑mj∑n[(rij−uivjT)2+λ(∣∣ui∣∣2+∣∣vj∣∣2)]
其中:λ 为正则项系数
隐式反馈代价函数
隐式反馈对应的ALS算法即:ALS-WR(Alternating Least Squares With Weighted-λ -regularization)
很多情况下,用户并没有明确反馈对物品的偏好,需要通过用户的相关行为去推测其对物品的偏好,比如在电商网站中,用户是否点击物品,点击的话在一定程度上表示喜欢,未点击的话可能是不喜欢,也可能是没有看到该物品。这种形式下的反馈就被称为隐式反馈。即矩阵R为隐式反馈矩阵,引入变量p_ij表示用户u_i对物品v_j的置信度,如果隐式反馈大于0,置信度为,反之置信度为0。
p i j = { 1 r i j > 0 0 r i j = 0 p_{ij} = \left\{\begin{matrix} 1 & r_{ij} >0 \\ 0 & r_{ij} =0 \end{matrix}\right. pij={10rij>0rij=0
上文也提到了,隐式反馈为0,不代表用户完全不喜欢,也可能是用户没有看到该物品。另外用户点击一个物品,也不代表是喜欢他,可能是误点,所以需要一个信任等级来显示用户喜欢某个物品,一般情况下,r_ij越大(用户行为的次数),越能暗示用户喜欢某个物品,因此引入变量c_ij,来衡量p_ij的信任度。
c i j = 1 + α r i j c_{ij} = 1 + \alpha r_{ij} cij=1+αrij
α 为置信度系数,那么代价函数变为如下形式:
J ( U , V ) = ∑ i m ∑ j n [ c i j ( p i j − u i v j T ) 2 + λ ( ∣ ∣ u i ∣ ∣ 2 + ∣ ∣ v j ∣ ∣ 2 ) ] J(U,V) = \sum_{i}^{m} \sum_{j}^{n}[c_{ij}(p_{ij} - u_iv_j^T) ^2 + \lambda ( ||u_i||^2 + ||v_j||^2 ) ] J(U,V)=i∑mj∑n[cij(pij−uivjT)2+λ(∣∣ui∣∣2+∣∣vj∣∣2)]
算法求解
无论是隐式代价函数求解还是显式代价函数求解,他们都是凸函数,而且变量耦合在一起,常规的梯度下降算法不能求解。但是先固定U求V,再固定V求U,如此迭代下去,问题就可以解决了。
U 0 → V 1 → U 1 → V 2 → U 2 . . . . U^0 \rightarrow V^1 \rightarrow U^1 \rightarrow V^2 \rightarrow U^2 .... U0→V1→U1→V2→U2....
固定一个变量,求另外一个变量,用什么方法求解呢?梯度下降?可以,但是比较麻烦。这其实是一个最小二乘的问题,由于一般隐含的特征k不会太大,可以直接当做是正规方程去解决。如此的交替的使用最小二乘去求解,所以名字就叫做交替最小二乘法。
显氏反馈求解
固定V求解U,对公式进行求导化简,可得:
U T = ( V T V + λ I ) − 1 V T R T U ^T = \left( V^T V + \lambda I \right)^{-1} V^T R^T UT=(VTV+λI)−1VTRT
同理,固定U求解V,对公式进行求导化简,可得:
V T = ( U T U + λ I ) − 1 U T R V ^T = \left( U^T U + \lambda I \right)^{-1} U^T R VT=(UTU+λI)−1UTR
隐式反馈求解
固定V求解U,对公式进行求导化简,可得:
U T = ( V T C v V + λ I ) − 1 V T C v R T U ^T = \left( V^T C_v V + \lambda I \right)^{-1} V^T C_v R^T UT=(VTCvV+λI)−1VTCvRT
同理,固定U求解V,对公式进行求导化简,可得:
V T = ( U T C u U + λ I ) − 1 U T C u R V ^T = \left( U^T C_u U + \lambda I \right)^{-1} U^T C_u R VT=(UTCuU+λI)−1UTCuR
面试点
- 最小二乘法英文名字是什么?解释及其对应的数学原理
Least Squares
参考上文
- ALS全称是什么?为什么叫交替最小二乘法?
Alternaing Least Squares
参考上文
- 隐式反馈和显氏反馈的区别?两种形式下ALS的代价函数
《推荐系统开发实战》中有对其的介绍
两种形式下的代价函数参考上文
- 代价函数中的正则项及其含义?
参考上文
- 过拟合和欠拟合的含义?在ALS中什么情况会出现过拟合和欠拟合?对应的解决办法?
欠拟合定义:拟合的函数与训练集误差较大,
过拟合定义:拟合的函数与训练集完美匹配(误差很小)
合适拟合定义:拟合的函数与训练集误差较小
欠拟合出现原因:数据规模太小,特征太多,正则化项系数较小
过拟合出现原因:数据特征太少,正则化项系数较大
欠拟合解决办法:增大数据规模、减小数据特征数(维数)、增大正则化系数λ
过拟合解决办法:增多数据特征数、添加高次多项式特征、减小正则化系数λ
- Spark实现ALS可调节的参数有哪些?分别表示什么含义?
maxIters // 最大迭代次数,默认10
rank // 隐向量的长度,默认是10,一般远小于m,n
numBlocks // 数据分区的个数,默认是10
regParam // ALS中的正则化参数,默认是1.0
alpha // ALS隐氏反馈变量的参数,置信度系数,默认是1.0
userCol // 用户列名
itemCol // item列名
rateCol // 评分列名
implicitPrefs // 显氏反馈 还是 隐氏反馈,默认false,意味显氏反馈

【搜索与推荐Wiki】专注于搜索和推荐系统,尝试使用算法去更好的服务于用户,包括但不局限于机器学习,深度学习,强化学习,自然语言理解,知识图谱,还不定时分享技术,资料,思考等文章!