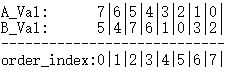Mike and distribution
Description:
Mike has always been thinking about the harshness of social inequality. He's so obsessed with it that sometimes it even affects him while solving problems. At the moment, Mike has two sequences of positive integers A = [a1, a2, ..., an] and B = [b1, b2, ..., bn] of length n each which he uses to ask people some quite peculiar questions.
To test you on how good are you at spotting inequality in life, he wants you to find an "unfair" subset of the original sequence. To be more precise, he wants you to select k numbers P = [p1, p2, ..., pk] such that 1 ≤ pi ≤ n for 1 ≤ i ≤ k and elements in P are distinct. Sequence P will represent indices of elements that you'll select from both sequences. He calls such a subset P "unfair" if and only if the following conditions are satisfied: 2·(ap1 + ... + apk) is greater than the sum of all elements from sequence A, and 2·(bp1 + ... + bpk) is greater than the sum of all elements from the sequence B. Also, k should be smaller or equal to because it will be to easy to find sequence P if he allowed you to select too many elements!
Mike guarantees you that a solution will always exist given the conditions described above, so please help him satisfy his curiosity!
InputThe first line contains integer n (1 ≤ n ≤ 105) — the number of elements in the sequences.
On the second line there are n space-separated integers a1, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.
On the third line there are also n space-separated integers b1, ..., bn (1 ≤ bi ≤ 109) — elements of sequence B.
On the first line output an integer k which represents the size of the found subset. k should be less or equal to .
On the next line print k integers p1, p2, ..., pk (1 ≤ pi ≤ n) — the elements of sequence P. You can print the numbers in any order you want. Elements in sequence Pshould be distinct.
5 8 7 4 8 3 4 2 5 3 7
3 1 4 5
公式变形:
2*X > X+Y ===> X>Y (X为选中下标在数组中对应的数之和,Y为未选中下标在数组中对应的数之和)
解题思想:
本质上就是要找出n/2+1个数,并且对于这个选中集合里面的数,在非选中的数中都能分别找到一个与之对应的小于它的数(所以这样的对应为两个数为一组,一个数来自选中集合,一个数来自非选中集合),这样就一定能保证选出数大于剩下没有选中的数,因为a>b ------> a*2 > a+b = sum(a为选中集合元素之和,b为非选中集合元素之和), 满足题目要求。例:1,4,9,6,5,2,选中9,4,5,非选中就是1,6,2,有9>6,4>1,5>2,所以这样选出的数就满足要求。(这里能看出来每组case解法可能有多种)
解题步骤:
对其中任意一个数组排序,这里就选A数组。原始的时候,A、B数组的元素是一一对应的,在对A数组排序的时候,对应的B数组的元素也要跟着A数组的元素一起移动。
这里order是个结构体数组
1.排完序之后,先把order[0]加进选中集合。
2.然后对order数组两个元素作为一个划分,即12,34, 56,7。
3.每一个划分里面选一个元素出来,选择规则为:选择B值大的那个元素。如此,选中的order下标就是0,2,3,6,7。然后找到对应的原始下标就可以了。
解释:
对于B数组,很显然第3步就能保证满足我们找到 a>b对 的思想,因为在每个二元素划分里面选出大的那个数的时候,就已经有了一个对应的比它小的数。
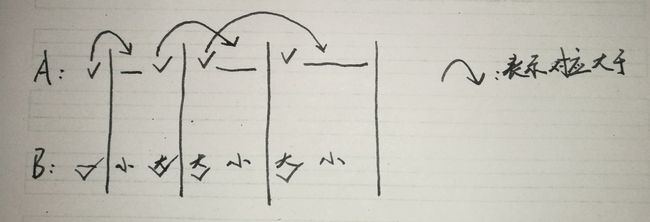
对于A数组,我们找每一对a>b就不像B数组一样在同一个划分里面找,而是跨划分找,如图所示。因为A数组是排了序的,所以这样跨划分的比较是一定满足a>b的。(√表示选中,_表示不选)。
两个数组都满足了,那么解也就满足了。
代码:
#include
#define INF 0x3f3f3f3f
#define LL long long
#define PI acos(-1.0)
using namespace std;
struct node
{
int a,b,f;
} arr[100005];
bool cmp(node x, node y)
{
return x.a>y.a;
}
int main()
{
int n;
while(~scanf("%d",&n))
{
for(int i=0; iarr[i+1].b)
printf(" %d",arr[i].f);
else
printf(" %d",arr[i+1].f);
}
printf("\n");
}
return 0;
}//FROM CJZ