使用python实现ACO解决ATT48
关键词:python、ACO(蚁群算法)、TSP(旅行商问题)、ATT48
参考文献:M. Dorigo, V. Maniezzo, and A. Colorni. The Ant System: An autocatalytic optimizing process. Technical Report 91-016 Revised, Dipartimento di Elettronica,Politecnico di Milano, Italy, 1991.
M. Dorigo and L. M. Gambardella. Ant colonies for the traveling salesman problem. BioSystems, 43:73–81, 1997.
可达att48数据集伪欧几里得距离最优值10628的解,欧几里得距离最优值33523的解
数据集:ATT48 https://wwwproxy.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/tsp/
city_data.txt
1 6734 1453
2 2233 10
3 5530 1424
4 401 841
5 3082 1644
6 7608 4458
7 7573 3716
8 7265 1268
9 6898 1885
10 1112 2049
11 5468 2606
12 5989 2873
13 4706 2674
14 4612 2035
15 6347 2683
16 6107 669
17 7611 5184
18 7462 3590
19 7732 4723
20 5900 3561
21 4483 3369
22 6101 1110
23 5199 2182
24 1633 2809
25 4307 2322
26 675 1006
27 7555 4819
28 7541 3981
29 3177 756
30 7352 4506
31 7545 2801
32 3245 3305
33 6426 3173
34 4608 1198
35 23 2216
36 7248 3779
37 7762 4595
38 7392 2244
39 3484 2829
40 6271 2135
41 4985 140
42 1916 1569
43 7280 4899
44 7509 3239
45 10 2676
46 6807 2993
47 5185 3258
48 3023 1942
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinedata_file = "city_data.txt"
def load_data(data_file):
res = []
with open(data_file) as f_obj:
for item in f_obj:
if len(item.strip())!=0:
res.append(item.split())
return np.array(res).astype('int')
def cal_distances(data):
a = data[:,1:].reshape(-1,2,1)
b = data[:,1:].T
c = np.sqrt(np.sum(np.square(a-b),axis=-2))
return c
city_loc = load_data(data_file)
distances = cal_distances(city_loc)def show_map(seq):
seq = np.array(seq)
data = city_loc
x = data[:,1]
y = data[:,2]
plt.scatter(x,y,marker=".")
city = data[np.append(seq,seq[0])]
plt.plot(city[:,1],city[:,2])
plt.show()city_num = distances.shape[0]
visibility = 1/(distances+0.01)
class Ant():
def __init__(self, init_pos):
self.init_pos = init_pos
self.tabu = [init_pos]
self.cur_pos = init_pos
self.distance = None
def init_tabu(self):
self.tabu = [self.init_pos]
self.distance = None
self.cur_pos = self.init_pos
def get_prob(self, alpha, belta, trail, visibility):
mask = np.ones(city_num)
mask[self.tabu] = 0
prob = (((trail[self.cur_pos]+1e-6)**alpha)*(visibility[self.cur_pos]**belta))*mask
assert np.all(np.isnan(prob)==False)
assert np.sum(prob)!=0
return prob
def acs_select_next(self, alpha, belta, trail, visibility,q0=0):
q = np.random.random()
prob = self.get_prob(alpha, belta, trail, visibility)
if qr:
return i
assert False
def cal_distance(self):
temp = np.array(self.tabu)
self.distance = np.sum(distances[temp[:-1],temp[1:]])
return self.distance
def move_to(self,city):
self.tabu.append(city)
self.cur_pos = city
class ACO_cycle():
def __init__(self):
self.trail = None
self.visibility = None
def run(self, epochs=100, alpha=1, belta=10, keep_rate=0.5, Q=100, distances=distances, verbose=True):
self.trail = np.ones((city_num, city_num))
self.visibility = 1/(distances+1e-6)
ants = [Ant(i) for i in range(city_num)]
# ants = [Ant(np.random.randint(0,city_num)) for i in range(196)]
shortest_Ls = []
avg_distances = []
solution = None
solution_L = 1e8
for i in range(epochs):
for t in range(city_num):
for ant in ants:
if t==city_num-1:
next_pos = ant.init_pos
else:
next_pos = ant.select_next(alpha, belta, self.trail, self.visibility)
ant.move_to(next_pos)
delta_trail = np.zeros((city_num,city_num))
avg_distance = 0
shortest_L = 1e8
path = None
for ant in ants:
L = ant.cal_distance()
avg_distance += L
if shortest_L > L:
shortest_L = L
path = ant.tabu
if solution_L > L:
solution = ant.tabu
solution_L = L
ant.init_tabu()
for ax, ay in zip(path[:-1],path[1:]):
delta_trail[ax,ay] += Q/shortest_L
delta_trail[ay,ax] += Q/shortest_L
avg_distances.append(avg_distance/len(ants))
shortest_Ls.append(shortest_L)
self.trail = keep_rate*self.trail + delta_trail
if verbose:
print("average distance",avg_distances[-1],"shortest distance",shortest_Ls[-1])
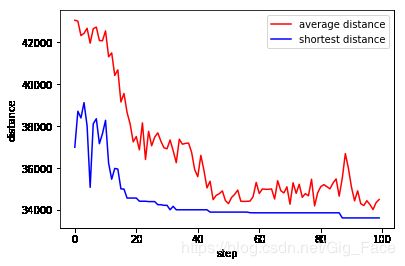
Y1 = avg_distances
Y2 = shortest_Ls
X = np.arange(len(Y1))
plt.xlabel('step')
plt.ylabel('distance')
plt.plot(X,Y1,label = "average distance",color = "r")
plt.plot(X,Y2,label = "shortest distance",color ="b")
plt.legend(loc="best")
plt.show()
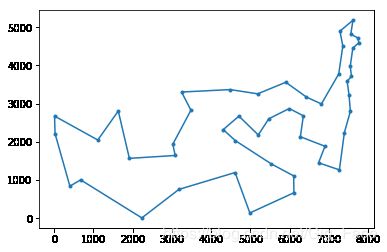
show_map(solution)
print("distance:",solution_L)
return solution_L, solution
model = ACO_cycle()
model.run(epochs=100,alpha=1,belta=10,keep_rate=0.5)distance: 33627.812773240636 [22, 10, 11, 14, 39, 8, 0, 7, 37, 30, 43, 17, 6, 27, 5, 36, 18, 26, 16, 42, 29, 35, 45, 32, 19, 46, 20, 31, 38, 47, 4, 41, 23, 9, 44, 34, 3, 25, 1, 28, 33, 40, 15, 21, 2, 13, 24, 12, 22]
class ACS():
def __init__(self):
self.trail = None
self.visibility = None
def run(self, epochs=100, alpha=1, belta=10, keep_rate=0.5, Q=98, distances=distances,q0=0.1, verbose=True):
self.trail = np.ones((city_num, city_num))
self.visibility = 1/(distances+1e-6)
ants = [Ant(i) for i in range(city_num)]
# ants = [Ant(np.random.randint(0,city_num)) for i in range(196)]
shortest_Ls = []
avg_distances = []
solution = None
solution_L = 1e8
for i in range(epochs):
for t in range(city_num):
for ant in ants:
if t==city_num-1:
next_pos = ant.init_pos
else:
next_pos = ant.acs_select_next(alpha, belta, self.trail, self.visibility,q0)
ant.move_to(next_pos)
delta_trail = np.zeros((city_num,city_num))
avg_distance = 0
shortest_L = 1e8
path = None
for ant in ants:
L = ant.cal_distance()
for ax, ay in zip(ant.tabu[:-1],ant.tabu[1:]):
delta_trail[ax,ay] += 1/(L*len(ants))
delta_trail[ay,ax] += 1/(L*len(ants))
avg_distance += L
if shortest_L > L:
shortest_L = L
path = ant.tabu
if solution_L > L:
solution = ant.tabu
solution_L = L
ant.init_tabu()
self.trail = keep_rate*self.trail + (1-keep_rate)*delta_trail
delta_trail = np.zeros((city_num,city_num))
for ax, ay in zip(path[:-1],path[1:]):
delta_trail[ax,ay] += Q/shortest_L
delta_trail[ay,ax] += Q/shortest_L
avg_distances.append(avg_distance/len(ants))
shortest_Ls.append(shortest_L)
self.trail = keep_rate*self.trail + (1-keep_rate)*delta_trail
if verbose:
print("average distance",avg_distances[-1],"shortest distance",shortest_Ls[-1])
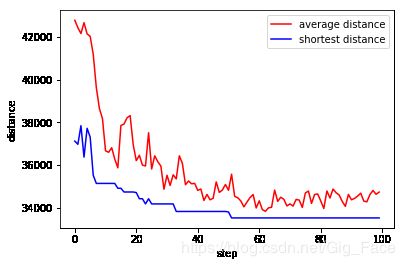
Y1 = avg_distances
Y2 = shortest_Ls
X = np.arange(len(Y1))
plt.xlabel('step')
plt.ylabel('distance')
plt.plot(X,Y1,label = "average distance",color = "r")
plt.plot(X,Y2,label = "shortest distance",color ="b")
plt.legend(loc="best")
plt.show()
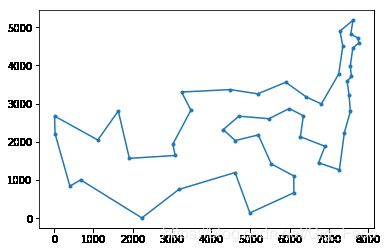
show_map(solution)
print("distance:",solution_L)
return solution_L, solution
model = ACS()
model.run(epochs=100,alpha=1,belta=10, keep_rate=0.5)distance: 33523.708507435585 [0, 8, 39, 14, 11, 10, 12, 24, 13, 22, 2, 21, 15, 40, 33, 28, 1, 25, 3, 34, 44, 9, 23, 41, 4, 47, 38, 31, 20, 46, 19, 32, 45, 35, 29, 42, 16, 26, 18, 36, 5, 27, 6, 17, 43, 30, 37, 7, 0]