编辑距离算法（Edit Distance）
写在前面的话
今年是2016年的最后一天，外公，超级想你，我都没有想过你会不能继续再走到2017.我过得很好，每天都超级幸福，我现在在学校有一堆好朋友。哈哈，我总是能处在宇宙中心的那种人，没办法，您这么优秀才能教出这么好的孙女，好吧。
我会好好学习的，我是第一女王嘛，永远都会是的。是吧，要做就做最好，要么就不做，我永远都要做你的骄傲。对了，我又有很多新朋友了，我们就像家人一样，就是每天都过得超级幸福，哈哈，就是有种魔力，能让我遇到的人都把像家人一样对待。我又变美了，好吧，简直是全院最美的，好吧。现在有一堆人在照顾我，保护我，给我开心，带我给无穷无尽的快乐，我从来都没有这么开心过。生命真的很奇特，不是么。
啊，对了，隆达罗西复出了，我们等了好久，你在天国要记得看知道么。还有啊，要照顾好自己。我爱你哟，你知道超级爱～
好像这个月写的都是传说中的"情感"博客，看不下去了，出来写篇非情感博客。
好像我的技术博客情感博客变成了主线，技术博客变成了背景衬托，哈哈哈，心疼的抱抱订阅我博客的小伙伴们。
感觉最近打字真的很顺溜啊。哟西，速度真的是杠杠滴
终于可以不正紧的写一篇技术博客了，画风突然有点奇特，嘎嘎嘎～
概念
编辑距离的作用主要是用来比较两个字符串的相似度的
基本的定义如下所示：
编辑距离，又称Levenshtein距离（莱文斯坦距离也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。
这个概念是由俄罗斯科学家Vladimir Levenshtein在1965年提出来的，所以也叫 Levenshtein 距离。它可以用来做DNA分析，拼字检测，抄袭识别等等。总是比较相似的，或多或少我们可以考虑编辑距离。
在概念中，我们可以看出一些重点那就是，编辑操作只有三种。插入，删除，替换这三种操作，我们有两个字符串，将其中一个字符串经过上面的这三种操作之后，得到两个完全相同的字符串付出的代价是什么就是我们要讨论和计算的。
例如：
我们有两个字符串： kitten 和 sitting:
现在我们要将kitten转换成sitting
我们可以做如下的一些操作；
k i t t e n --> s i t t e n 将K替换成S
sitten --> sittin 将 e 替换成i
sittin --> sitting 添加g
在这里我们设置每经过一次编辑，也就是变化（插入，删除，替换）我们花费的代价都是1。
例如：
- 如果str1=“ivan”，str2=“ivan”，那么经过计算后等于 0。没有经过转换。相似度=1-0/Math.Max(str1.length,str2.length)=1
- 如果str1=“ivan1”，str2=“ivan2”，那么经过计算后等于1。str1的"1"转换"2"，转换了一个字符，所以距离是1，相似度=1-1/Math.Max(str1.length,str2.length)=0.8
#算法过程
1.str1或str2的长度为0返回另一个字符串的长度。 if(str1.length0) return str2.length; if(str2.length0) return str1.length;
2.初始化(n+1)(m+1)的矩阵d，并让第一行和列的值从0开始增长。扫描两字符串（nm级的），如果：str1[i] == str2[j]，用temp记录它，为0。否则temp记为1。然后在矩阵d[i,j]赋于d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。
3.扫描完后，返回矩阵的最后一个值d[n][m]即是它们的距离。
计算相似度公式：1-它们的距离/两个字符串长度的最大值。
其实这个算法并不难实现
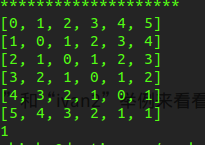
我们用字符串“ivan1”和“ivan2”举例来看看矩阵中值的状况：
1、第一行和第一列的值从0开始增长
图一
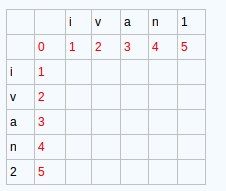
首先我们先创建一个矩阵，或者说是我们的二维数列，假设有两个字符串，我们的字符串的长度分别是m和n，那么，我们矩阵的维度就应该是(m+1)*(n+1).
注意，我们先给数列的第一行第一列赋值，从0开始递增赋值。我们就得到了图一的这个样子
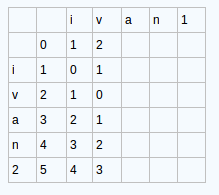
之后我们计算第一列，第二列，依次类推，算完整个矩阵。
我们的计算规则就是：
d[i,j]=min(d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp) 这三个当中的最小值。
其中：str1[i] == str2[j]，用temp记录它，为0。否则temp记为1
我们用d[i-1,j]+1表示增加操作
d[i,j-1]+1 表示我们的删除操作
d[i-1,j-1]+temp表示我们的替换操作
2、举证元素的产生 Matrix[i - 1, j] + 1 ; Matrix[i, j - 1] + 1 ; Matrix[i - 1, j - 1] + t 三者当中的最小值
3.依次类推直到矩阵全部生成
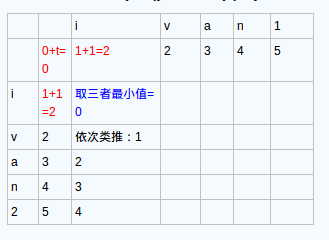
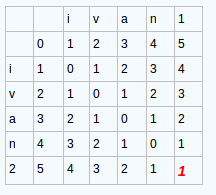
这个就得到了我们的整个完整的矩阵。
下面我们来看下代码，我最擅长的就是Python，下面我们来看实现：
#!/usr/bin/env python
# coding=utf-8
# function : calculate the minEditDistance of two strings
# author : Chicho
# date : 2016-12-31
def minEditDist(sm,sn):
m,n = len(sm)+1,len(sn)+1
# create a matrix (m*n)
matrix = [[0]*n for i in range(m)]
matrix[0][0]=0
for i in range(1,m):
matrix[i][0] = matrix[i-1][0] + 1
for j in range(1,n):
matrix[0][j] = matrix[0][j-1]+1
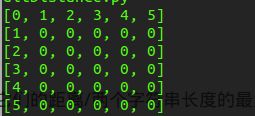
for i in range(m):
print matrix[i]
print "********************"
cost = 0
for i in range(1,m):
for j in range(1,n):
if sm[i-1]==sn[j-1]:
cost = 0
else:
cost = 1
matrix[i][j]=min(matrix[i-1][j]+1,matrix[i][j-1]+1,matrix[i-1][j-1]+cost)
for i in range(m):
print matrix[i]
return matrix[m-1][n-1]
mindist=minEditDist("ivan1","ivan2")
print mindist
我们来看下最后得到的运行结果：
上面是一个初始化的矩阵
最后得到的结果，距离就是最后右下角的那个值1
下面我们在根据计算出两个字符串的相似度：
最后得到它们的距离=1
相似度：1-1/Math.Max(“ivan1”.length,“ivan2”.length) =0.8
参考文献：
http://www.cnblogs.com/ivanyb/archive/2011/11/25/2263356.html
写在后面的话
无意中发现了一个巨牛的人工智能教程，忍不住分享一下给大家。教程不仅是零基础，通俗易懂，而且非常风趣幽默，像看小说一样！觉得太牛了，所以分享给大家。点这里可以跳转到教程 https://www.cbedai.net/chichoxian
外公，爱你，给你一个敲大的么么哒
希望生命可以产生所有奇妙的化学反应