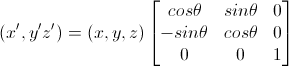几何变换

几何变换详解
在三维图形学中，几何变换大致分为三种，平移变换（Translation），缩放变换（Scaling），旋转变换（Rotation）。以下讨论皆针对DirectX，所以使用左手坐标系。

平移变换

将三维空间中的一个点[x, y, z, 1]移动到另外一个点[x’, y’, z’, 1]，三个坐标轴的移动分量分别为dx=Tx, dy=Ty, dz=Tz, 即

x’ = x + Tx

y’ = y + Ty

z’ = z + Tz

平移变换的矩阵如下。

缩放变换

将模型放大或者缩小，本质也是对模型上每个顶点进行放大和缩小（顶点坐标值变大或变小），假设变换前的点是[x, y, z, 1]，变换后的点是[x’, y’, z’, 1]，那么

x’ = x * Sx

y’ = y * Sy

z’ = z * Sz

缩放变换的矩阵如下。

旋转变换

这是三种变换中最复杂的变换，这里只讨论最简单的情况，绕坐标轴旋转，关于绕任意轴旋转，在后续的随笔中介绍。

绕X轴旋转

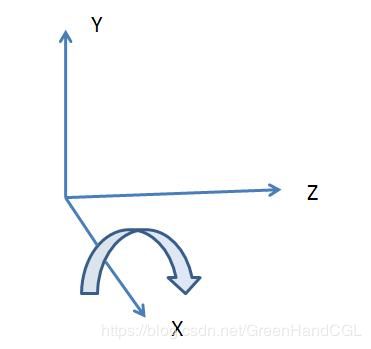
绕X轴旋转时，顶点的x坐标不发生变化，y坐标和z坐标绕X轴旋转θ度，旋转的正方向为顺时针方向（沿着旋转轴负方向向原点看）。[x, y, z, 1]表示变换前的点，[x’, y’, z’, 1]表示变换后的点。变换矩阵如下。关于旋转的正方向，OpenGL与多数图形学书籍规定旋转正方向为逆时针方向（沿着坐标轴负方向向原点看），比如Computer Graphics C Version，p409。

绕Y轴旋转

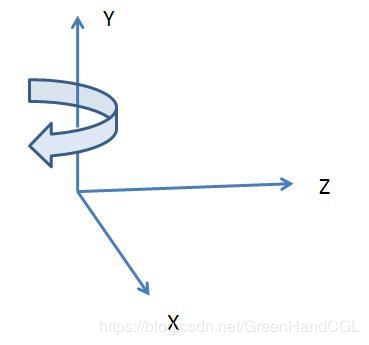
绕Y轴旋转时，顶点的y坐标不发生变化，x坐标和z坐标绕Y轴旋转θ度。[x, y, z, 1]表示变换前的点，[x’, y’, z’, 1]表示变换后的点。变换矩阵如下。

绕Z轴旋转

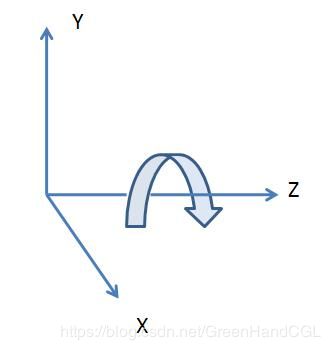
绕Z轴旋转时，顶点的z坐标不发生变化，x坐标和y坐标绕Z轴旋转θ度。[x, y, z, 1]表示变换前的点，[x’, y’, z’, 1]表示变换后的点。变换矩阵如下。

绕坐标轴旋转的矩阵推导
上面三个旋转矩阵是如何得来的呢？我们推导一下，首先看一下二维的情况，再扩展到三维即可。实际上上面三种绕坐标轴旋转的情况属于特殊的二维旋转，比如绕Z轴旋转，相当于在与XOY平面上绕原点做二维旋转。

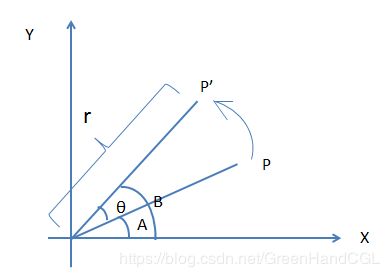
假设点P(x, y)是平面直角坐标系内一点，其到原点的距离为r，其与X轴的夹角为A，现将点P绕原点旋转θ度，得到点P’(x’, y’)，P’与X轴的夹角为B，则A = B - θ。（注意，在二维坐标中，逆时针旋转时角度为正，顺时针旋转时角度为负，下图中由P旋转到P’，角度为θ，若是由P’转到P，则角度为-θ）。

于是可得下面的转换方程

（式一）

写成矩阵的形式就是

求得旋转矩阵为

由于这里使用齐次坐标，所以还需加上一维，最终变成如下形式（绕Z轴旋转矩阵）

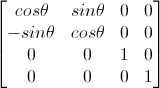
和前面给出的绕Z轴旋转矩阵完全吻合。

对于绕X轴旋转的情况，我们只需将式一中的x用y替换，y用z替换，z用x替换即可。替换后得到
(式二)
对应的旋转矩阵为（绕X轴旋转矩阵）：

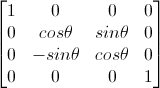
对于绕Y轴旋转的情况，只需对式二做一次同样的替换即可，的到的变换方程为

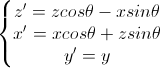
对应的变换矩阵为（绕Y轴旋转矩阵）：

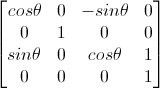
逆矩阵

平移变换矩阵的逆矩阵与原来的平移量相同，但是方向相反。

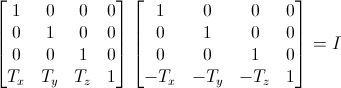
旋转变换矩阵的逆矩阵与原来的旋转轴相同但是角度相反。

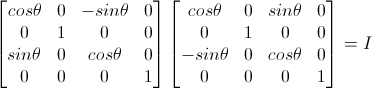
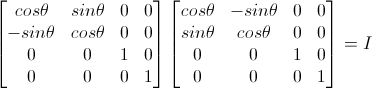
缩放变换的逆矩阵正好和原来的效果相反，如果原来是放大，则逆矩阵是缩小，如果原来是缩小，则逆矩阵是放大。

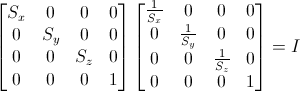
作者：zdd
出处：http://www.cnblogs.com/graphics/

---

动动小手

#include "rotate.h"

bool rotate_Z(pcl::PointCloud<pcl::PointXYZ>::Ptr cloud, pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_rotated, float theta)
{
	/* Reminder: how transformation matrices work :
	|-------> This column is the translation
	| cos(theta) -sin(theta) 0 x |  \
	| sin(theta)  cos(theta) 0 y |   }-> The identity 3x3 matrix (Z axis) on the left
	| 0           0          1 z |  /
	| 0           0          0 1 |    -> We do not use this line (and it has to stay 0,0,0,1)

	This is the "manual" method, perfect to understand but error prone !
	*/

	Eigen::Matrix4f transform = Eigen::Matrix4f::Identity();
	//float theta = M_PI / 2;
	transform(0, 0) = cos(theta);
	transform(0, 1) = -sin(theta);
	transform(1, 0) = sin(theta);
	transform(1, 1) = cos(theta);
	pcl::transformPointCloud(*cloud, *cloud_rotated, transform);
	
	return true;
}

bool rotate_X(pcl::PointCloud<pcl::PointXYZ>::Ptr cloud, pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_rotated, float theta)
{
	/* Reminder: how transformation matrices work :
	|-------> This column is the translation
	| 1 0           0          x |  \
	| 0 cos(theta)  sin(theta) y |   }-> The identity 3x3 matrix (X axis) on the left
	| 0 -sin(theta) cos(theta) z |  /
	| 0 0           0          1 |    -> We do not use this line (and it has to stay 0,0,0,1)

	This is the "manual" method, perfect to understand but error prone !
	*/

	Eigen::Matrix4f transform = Eigen::Matrix4f::Identity();
	//float theta = M_PI / 2;
	transform(1, 1) = cos(theta);
	transform(1, 2) = sin(theta);
	transform(2, 1) = -sin(theta);
	transform(2, 2) = cos(theta);
	pcl::transformPointCloud(*cloud, *cloud_rotated, transform);

	return true;
}

bool rotate_Y(pcl::PointCloud<pcl::PointXYZ>::Ptr cloud, pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_rotated, float theta)
{
	/* Reminder: how transformation matrices work :
	|-------> This column is the translation
	| cos(theta) 0          -sin(theta) x |  \
	| 0          1          0           y |   }-> The identity 3x3 matrix (Y axis) on the left
	| sin(theta) 0          cos(theta)  z |  /
	| 0          0          0           1 |    -> We do not use this line (and it has to stay 0,0,0,1)

	This is the "manual" method, perfect to understand but error prone !
	*/

	Eigen::Matrix4f transform = Eigen::Matrix4f::Identity();
	//float theta = M_PI / 2;
	transform(0, 0) = cos(theta);
	transform(0, 2) = -sin(theta);
	transform(2, 0) = sin(theta);
	transform(2, 2) = cos(theta);
	pcl::transformPointCloud(*cloud, *cloud_rotated, transform);

	return true;
}