机器学习之梯度下降
翻译|Gradient Descent in Python
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use(['ggplot'])当你初次涉足机器学习时,你学习的第一个基本算法就是 梯度下降 (Gradient Descent), 可以说梯度下降法是机器学习算法的支柱。 在这篇文章中,我尝试使用 python解释梯度下降法的基本原理。一旦掌握了梯度下降法,很多问题就会变得容易理解,并且利于理解不同的算法。
如果你想尝试自己实现梯度下降法, 你需要加载基本的 python packages —— numpy and matplotlib
首先, 我们将创建包含着噪声的线性数据
# 随机创建一些噪声
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)array([[1.33025881], [0.09309373], [0.49532139], [1.60476696], [0.58710846], [1.56722395], [0.59914427], [1.51932972], [1.13519401], [1.48989254]])
接下来通过 matplotlib 可视化数据
# 可视化数据
plt.plot(X, y, 'b.')
plt.xlabel("$x$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])显然, yy 与 xx 具有良好的线性关系,这个数据非常简单,只有一个自变量 xx.
我们可以将其表示为简单的线性关系:
y=b+mx
并求出 b , m。
这种被称为解方程的分析方法并没有什么不妥,但机器学习是涉及矩阵计算的,因此我们使用矩阵法(向量法)进行分析。
我们将 y 替换成 J(θ), b 替换成 θ0, m 替换成 θ1。
得到如下表达式:
J(θ)=θ0+θ1x
注意: 本例中 θ0=4, θ1=3
求解 θ0和 θ1的分析方法,代码如下:
X_b = np.c_[np.ones((100, 1)), X] # 为X添加了一个偏置单位,对于X中的每个向量都是1
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_bestarray([[4.0728819 ], [3.05958308]])
不难发现这个值接近真实的 θ0,θ1,由于我在数据中引入了噪声,所以存在误差。
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
y_predict = X_new_b.dot(theta_best)
y_predictarray([[ 3.86687149],
[10.11504826]])梯度下降法 (Gradient Descent)
Cost Function & Gradients
计算代价函数和梯度的公式如下所示。
注意:代价函数用于线性回归,对于其他算法,代价函数是不同的,梯度必须从代价函数中推导出来。
#定义cost函数
def cal_cost(theta, X, y):
'''
thete:θ的向量形式
X:输入数据
y:输出
'''
m = len(y)
predictions = X.dot(theta)#得到预测的结果
cost = (1/2*m) * np.sum(np.square(predictions - y))
return cost
def gradient_descent(X, y, theta, learning_rate = 0.01, iterations = 100):
'''
X : X的矩阵,增加了偏置单位
y : 输出向量y
theta=Vector of thetas np.random.randn(j,1)
learning_rate 学习率
iterations #迭代轮数
返回最终的theta向量和成本历史数组,而不是迭代次数
'''
m = len(y)
cost_history = np.zeros(iterations)#np.zeros(iterations)表示生成iterations*1的全0矩阵
theta_history = np.zeros((iterations, 2))#表示生成iterations*2的全0矩阵
for i in range(iterations):
prediction = np.dot(X, theta) #由输入x和随机生成的参数theta:θ对结果预测存储在prediction
#参数更新
theta = theta - (1/m) * learning_rate * (X.T.dot((prediction - y)))#X.T将矩阵X转置与(prediction - y)做矩阵乘法
theta_history[i, :] = theta.T #将每一次迭代得到的theta共iterations轮,存储在theta_history中,便于观察变化过程
cost_history[i] = cal_cost(theta, X, y)#用自定义的损失函数cal_cost计算每一次迭代的损失函数的值存储在cost_history中
return theta, cost_history, theta_history# 从1000次迭代开始,学习率为0.01。从高斯分布的θ开始
lr =0.01 #学习率
n_iter = 1000 #迭代轮数
theta = np.random.randn(2, 1)
X_b = np.c_[np.ones((len(X), 1)), X] #np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等.np.ones((len(X), 1))表示生成len(X)*1的1矩阵
theta, cost_history, theta_history = gradient_descent(X_b, y, theta, lr, n_iter)
print('Theta0: {:0.3f},\nTheta1: {:0.3f}'.format(theta[0][0],theta[1][0]))
print('Final cost/MSE: {:0.3f}'.format(cost_history[-1]))Theta0: 3.811,
Theta1: 3.294
Final cost/MSE: 4076.040
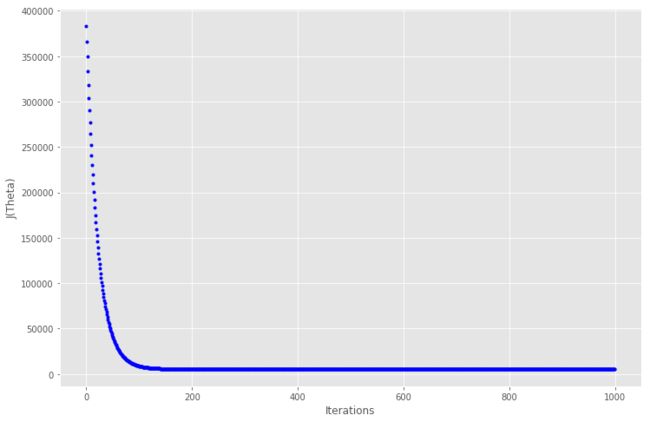
# 绘制迭代的成本图
fig, ax = plt.subplots(figsize=(12,8))#整个图像为一个Figure对象,包含一个或者多个Axes对象。此句代码指Axes对象为(12,8)
ax.set_ylabel('J(Theta)')
ax.set_xlabel('Iterations')
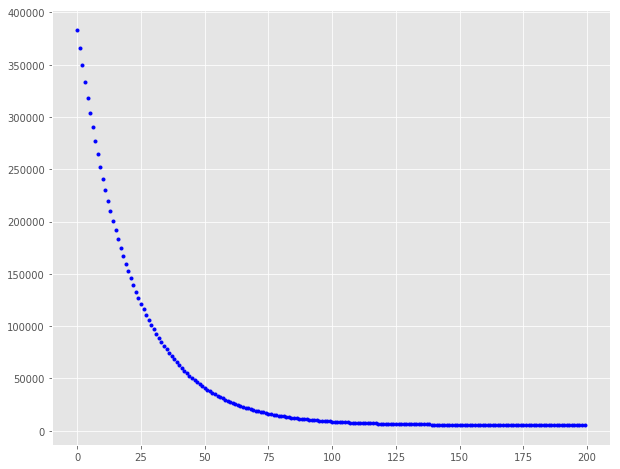
ax.plot(range(1000), cost_history, 'b.')在大约 150 次迭代之后代价函数趋于稳定,因此放大到迭代200,看看曲线
fig, ax = plt.subplots(figsize=(10,8))
ax.plot(range(200), cost_history[:200], 'b.')值得注意的是,最初成本下降得更快,然后成本降低的收益就不那么多了。 我们可以尝试使用不同的学习速率和迭代组合,并得到不同学习率和迭代的效果会如何。
让我们建立一个函数,它可以显示效果,也可以显示梯度下降实际上是如何工作的。
def plot_GD(n_iter, lr, ax, ax1=None):
'''
n_iter = no of iterations
lr = Learning Rate
ax = Axis to plot the Gradient Descent
ax1 = Axis to plot cost_history vs Iterations plot
'''
ax.plot(X, y, 'b.')
theta = np.random.randn(2, 1)
tr = 0.1
cost_history = np.zeros(n_iter)
for i in range(n_iter):
pred_prev = X_b.dot(theta)
theta, h, _ = gradient_descent(X_b, y, theta, lr, 1)
pred = X_b.dot(theta)
cost_history[i] = h[0]
if ((i % 25 == 0)):
ax.plot(X, pred, 'r-', alpha=tr)
if tr < 0.8:
tr += 0.2
if not ax1 == None:
ax1.plot(range(n_iter), cost_history, 'b.')
# 绘制不同迭代和学习率组合的图
fig = plt.figure(figsize=(30,25), dpi=200)#figsize:指定figure的宽和高,dpi参数指定绘图对象的分辨率
fig.subplots_adjust(hspace=0.4, wspace=0.4)#subplots_adjust方法可以修改间距,wspace和hspace用于控制宽度和高度的百分比
it_lr = [(2000, 0.001), (500, 0.01), (200, 0.05), (100, 0.1)]
count = 0
for n_iter, lr in it_lr:
count += 1
ax = fig.add_subplot(4, 2, count)#添加一个Axes对象到fig中
count += 1
ax1 = fig.add_subplot(4, 2, count)
ax.set_title("lr:{}" .format(lr))#图的标签
ax1.set_title("Iterations:{}" .format(n_iter))#图的标签
plot_GD(n_iter, lr, ax, ax1)
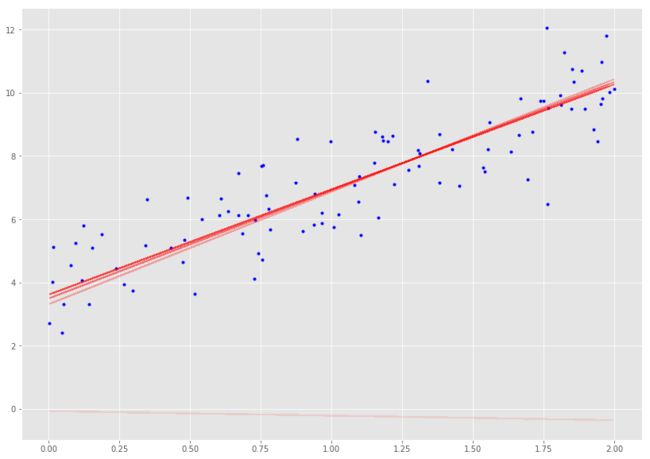
通过观察发现,以较小的学习速率收集解决方案需要很长时间,而学习速度越大,学习速度越快。
_, ax = plt.subplots(figsize=(14, 10))
plot_GD(100, 0.1, ax)随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的 m个样本的数据,而是仅仅选取一个样本 j来求梯度。对应的更新公式是:![]()
def stocashtic_gradient_descent(X, y, theta, learning_rate=0.01, iterations=10):
'''
X = Matrix of X with added bias units
y = Vector of Y
theta=Vector of thetas np.random.randn(j,1)
learning_rate
iterations = no of iterations
Returns the final theta vector and array of cost history over no of iterations
'''
m = len(y)
cost_history = np.zeros(iterations)#np.zeros(iterations)表示生成iterations*1的全0矩阵
for it in range(iterations):#迭代iterations
cost = 0.0
for i in range(m):
rand_ind = np.random.randint(0, m)
X_i = X[rand_ind, :].reshape(1, X.shape[1])
y_i = y[rand_ind, :].reshape(1, 1)
prediction = np.dot(X_i, theta)
theta -= (1/m) * learning_rate * (X_i.T.dot((prediction - y_i)))
cost += cal_cost(theta, X_i, y_i)
cost_history[it] = cost
return theta, cost_historylr =0.5 #学习率
n_iter = 50 #迭代轮数
theta = np.random.randn(2, 1)
X_b = np.c_[np.ones((len(X), 1)), X] #np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等.np.ones((len(X), 1))表示生成len(X)*1的1矩阵
theta, cost_history = stocashtic_gradient_descent(X_b, y, theta, lr, n_iter)
print('Theta0: {:0.3f},\nTheta1: {:0.3f}' .format(theta[0][0],theta[1][0]))
print('Final cost/MSE: {:0.3f}' .format(cost_history[-1]))Theta0: 4.009,
Theta1: 3.063
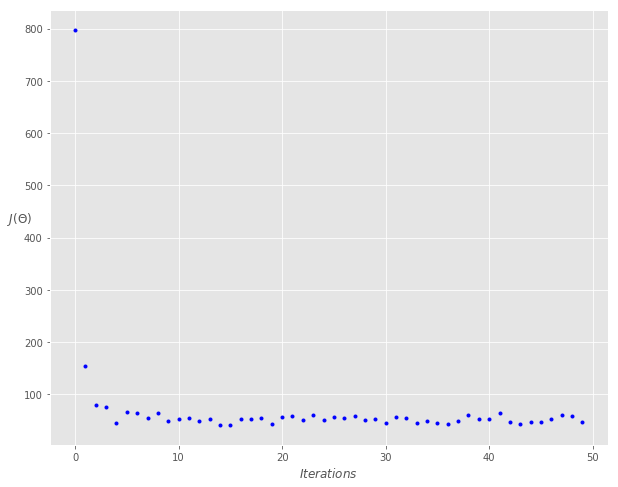
Final cost/MSE: 40.442fig, ax = plt.subplots(figsize=(10,8))
ax.set_ylabel('$J(\Theta)$' ,rotation=0)
ax.set_xlabel('$Iterations$')
theta = np.random.randn(2,1)
ax.plot(range(n_iter), cost_history, 'b.')
小批量梯度下降法(Mini-batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于 m 个样本,我们采用 x 个样子来迭代,1 用一句话概括就是,目标函数必须是凸函数。关于凸函数的判定,对于一元函数来说,一般是求二阶导数,若其二阶导数非负,就称之为凸函数。对于多元函数来说判定方法类似,只是从判断一元函数的单个二阶导数是否非负,变成了判断所有变量的二阶偏导数构成的黑塞矩阵(Hessian Matrix)是否为半正定矩阵。判断一个矩阵是否半正定可以判断所有特征值是否非负,或者判断所有主子式是否非负。 为了解决当目标函数是凹函数,在梯度下降法的基础上衍生出了各式各样的改进算法,例如动态调整步长(即学习率),利用上一次结果的动量法,以及随机梯度下降法(Stochastic Gradient Descent, SGD)等等。实际上,这些优化算法在当前最火热的深度学习中也占据着一席之地,例如adagrad、RMSprop,Adam等等。 随机梯度下降法主要是用来解决求和形式的优化问题. 转载:https://www.laugh12321.cn/2019/03/09/Gradient_Descent/#moredef minibatch_gradient_descent(X, y, theta, learning_rate=0.01, iterations=10, batch_size=20):
'''
X = Matrix of X without added bias units
y = Vector of Y
theta=Vector of thetas np.random.randn(j,1)
learning_rate
iterations = no of iterations
Returns the final theta vector and array of cost history over no of iterations
'''
m = len(y)
cost_history = np.zeros(iterations)
n_batches = int(m / batch_size)
for it in range(iterations):
cost = 0.0
indices = np.random.permutation(m)
X = X[indices]
y = y[indices]
for i in range(0, m, batch_size):
X_i = X[i: i+batch_size]
y_i = y[i: i+batch_size]
X_i = np.c_[np.ones(len(X_i)), X_i]
prediction = np.dot(X_i, theta)
theta -= (1/m) * learning_rate * (X_i.T.dot((prediction - y_i)))
cost += cal_cost(theta, X_i, y_i)
cost_history[it] = cost
return theta, cost_historylr = 0.1
n_iter = 200
theta = np.random.randn(2, 1)
theta, cost_history = minibatch_gradient_descent(X, y, theta, lr, n_iter)
print('Theta0: {:0.3f},\nTheta1: {:0.3f}' .format(theta[0][0], theta[1][0]))
print('Final cost/MSE: {:0.3f}' .format(cost_history[-1]))
Theta0: 4.035,
Theta1: 3.093
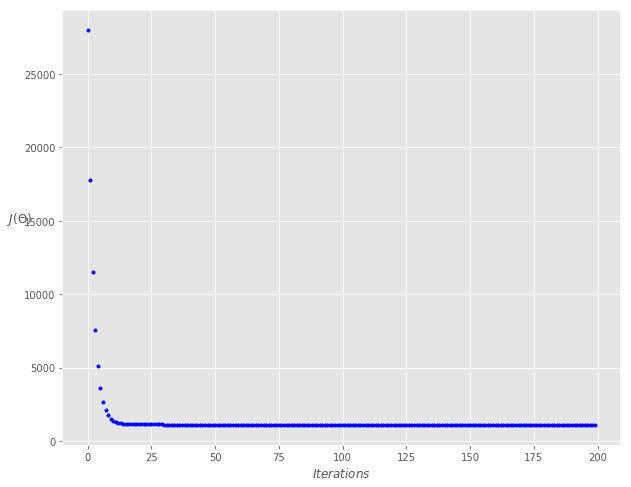
Final cost/MSE: 792.875 fig, ax = plt.subplots(figsize=(10,8))
ax.set_ylabel('$J(\Theta)$', rotation=0)
ax.set_xlabel('$Iterations$')
theta = np.random.randn(2, 1)
ax.plot(range(n_iter), cost_history, 'b.')
梯度下降的局限性: