Ceres库和g2o库的使用

1.Ceres库

Ceres库向通用的最小二乘问题的求解，定义优化问题，设置一些选项，可通过Ceres求解。 Ceres求解的最小二乘问题最一般形式为：

minx12∑ipi(||fi(xi1,⋯xin)||2),s.t.lj≤xj≤uj m i n x 1 2 ∑ i p i ( | | f i ( x i 1 , ⋯ x i n ) | | 2 ) , s . t . l j ≤ x j ≤ u j

在Ceres问题中，我们将定义优化变量 x x 和每个代价函数 fi f i , 再调用Ceres进行求解。可以使用高斯牛顿法或者列文伯格-马夸克特方法进行梯度下降，并设定梯度下降条件，Ceres会在优化之后将最优估计值返回。

假设有一个方程的曲线：

y=exp(ax2+bx+c)+w y = e x p ( a x 2 + b x + c ) + w

其中 a,b,c a , b , c 是曲线的参数， w w 为高斯噪声，这是一个非线性模型。假如我们有 N N 个关于 x，y x ， y 的观测数据点，想根据这些数据点求出曲线的参数。那么我们可以根据下面的最小二乘问题以估计曲线参数:

mina,b,c12∑Ni=1||yi−exp(ax2i+bxi+c)||2 m i n a , b , c 1 2 ∑ i = 1 N | | y i − e x p ( a x i 2 + b x i + c ) | | 2

通过代码求得以上结果：

#include 
#include 
#include 
#include 

using namespace std;

//代价函数的计算模型
struct Test_ceres
{
  Test_ceres (double x,double y):_x(x),_y(y) {}
  template <typename T>//避免重复定义
  bool operator()(const T* const abc,   // 模型参数，有3维
                   T* residual) const  // 残差
  {
    residual[0]=T(_y)-ceres::exp(abc[0]*T(_x)+abc[1]*T(_x)+abc[2]); // y-exp(ax^2+bx+c) 这就是误差
    return true;
  }
    const double _x,_y;  // x,y数据
 };


int main(int argc, char **argv)
{
  double a=1.0,b=2.0,c=1.0; //真实参数值
  int N=100;  //数据点
  double w_sigma=1.0;  //噪声Sigma值
  cv::RNG rng;   //openCv 随机数产生器
  double abc[3]={0,0,0}; //abc参数的估计值
  vector<double> x_data,y_data;
  cout<<"generating data:"<for(int i=0;idouble x=i/100.0;
    x_data.push_back(x);
 y_data.push_back(exp(a*x*x+b*x+c)+rng.gaussian(w_sigma));
    cout<<"x_data[i]"<<""<//构建最小二乘问题
  ceres::Problem problem;
  for(int i=0;i//向问题中添加误差项，使用自动求导，
                             //模板参数：误差类型，输出维度，输入维度，数值参照前面struct写法
                   new ceres::AutoDiffCostFunction1,3>(
          new Test_ceres(x_data[i],y_data[i]) ),
          nullptr,//核函数，这里不使用，所以为空
          abc    //待估计参数
        );
  }

//配置求解器
  ceres::Solver::Options option;
  option.linear_solver_type=ceres::DENSE_QR;//增量方程如何求解，利用高斯牛顿法还是马夸克—列文伯格等
  option.minimizer_progress_to_stdout=true;//输出到cout
  ceres::Solver::Summary summary;  //优化信息
  chrono::steady_clock::time_point t1=chrono::steady_clock::now();//计算前的时间
  ceres::Solve(option,&problem,&summary);//开始计算
  chrono::steady_clock::time_point t2=chrono::steady_clock::now();//计算后的时间
  chrono::duration<double> time_used=chrono::duration_castdouble>>(t2-t1);//求解一共所花的时间
  cout<<"solve time cost = "<"seconds."<//输出结果
  cout<cout<<"estimated a,b,c=";
  for (auto a:abc) cout<"";
  cout<return 0;
}

利用opencv生成100个带高斯噪声的数据，随后利用Ceres拟合，Ceres的用法如下:

1.定义了目标函数模型。定义方法为类。在类中使用了模板参数的()运算符，成为一个拟函数。
2.调用AddResidualBlock将误差项添加到目标函数中。由于优化需要梯度，在这里选择Auto Diff，即自动求导。
3.自动求导需要指定误差项和优化变量的维度，误差是标量，维度为1；优化的是a,b,c三个量，维度为3,。
4.设定后问题之后，调用solve函数进行求解，在options里可以选择配置。

2.g2o库

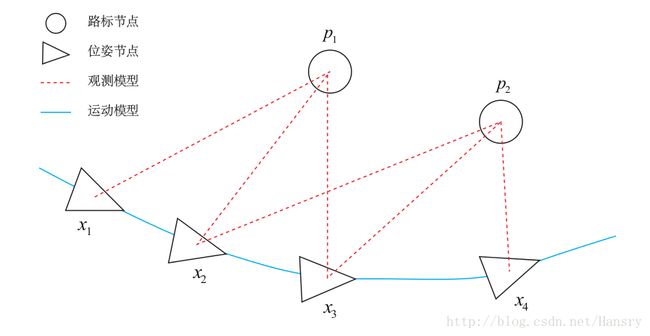
图优化，是把优化问题表现成图的一种方式，这里的图是图论意义上的图。一个图由若干个顶点,以及连着这些顶点的边组成。在这里，我们用顶点表示优化变量，而用边表示误差项。

构建图优化例子。用三角形表示相机位姿节点，用圆形表示路标点，它们构成了图优化的顶点。实线表示相机的运动模型，虚线表示观测模型，构成了图优化的边。

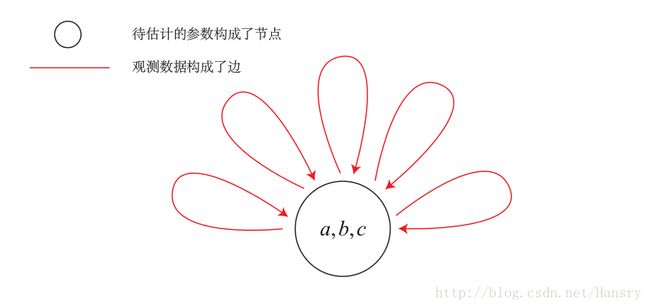
为了使用g2o,首先要将曲线拟合问题抽象成图优化。这个过程中，只要记住节点为优化变量，边为误差项即可。曲线拟合的图优化问题可以画成以下形式：

曲线拟合中，上述二乘问题参数a,b,c为优化变量，节点，带噪声数据点为误差项，即边。一元边，只有一个顶点，自己连自己。但是一条边可以连很多个点，代表这个误差项与多少个优化变量有关。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW  // 用到了new方法,指针对齐
    virtual void setToOriginImpl() // 重置
    {
        _estimate << 0,0,0;
    }
//顶点的更新函数，计算增量,在曲线拟合中，由于优化变量本身位于向量空间，这个更新确实就是简单的加法。若如果x是相机的位姿，则不是简单的加法了，需要自己定义了。
    virtual void oplusImpl( const double* update ) 
    {
        _estimate += Eigen::Vector3d(update);
    }
    // 存盘和读盘：留空
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    // 计算曲线模型误差，该函数需要取出边所连接的顶点的当前估计值，与观测值进行比较
    void computeError()
    {
        const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
public:
    double _x;  // x 值， y 值为 _measurement
};

int main( int argc, char** argv )
{
    double a=1.0, b=2.0, c=1.0;         // 真实参数值
    int N=100;                          // 数据点
    double w_sigma=1.0;                 // 噪声Sigma值
    cv::RNG rng;                        // OpenCV随机数产生器
    double abc[3] = {0,0,0};            // abc参数的估计值

    vector<double> x_data, y_data;      // 数据

    cout<<"generating data: "<for ( int i=0; idouble x = i/100.0;
        x_data.push_back ( x );
        y_data.push_back (
            exp ( a*x*x + b*x + c ) + rng.gaussian ( w_sigma )
        );
        cout<" "<// 构建图优化，先设定g2o
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;  // 每个误差项优化变量维度为3，误差值维度为1
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense(); // 线性方程求解器
    Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器
    // 梯度下降方法，从GN, LM, DogLeg 中选
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );
    // g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
    // g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
    g2o::SparseOptimizer optimizer;     // 图模型
    optimizer.setAlgorithm( solver );   // 设置求解器
    optimizer.setVerbose( true );       // 打开调试输出

    // 往图中增加顶点
    CurveFittingVertex* v = new CurveFittingVertex();
    v->setEstimate( Eigen::Vector3d(0,0,0) );
    v->setId(0);
    optimizer.addVertex( v ); //只有一个点

    // 往图中增加边
    for ( int i=0; inew CurveFittingEdge( x_data[i] );
        edge->setId(i);
        edge->setVertex( 0, v );                // 设置连接的顶点
        edge->setMeasurement( y_data[i] );      // 观测数值
        edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆
        optimizer.addEdge( edge );
    }

    // 执行优化
    cout<<"start optimization"<100);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_castdouble>>( t2-t1 );
    cout<<"solve time cost = "<" seconds. "<// 输出优化值
    Eigen::Vector3d abc_estimate = v->estimate();
    cout<<"estimated model: "<return 0;
}

3.小结

Ceres定义误差项求曲线拟合问题自然直观很多，本事即是一个优化库。提供了基于模板元的自动求导和运行时数值求导。

g2o，在SLAM过程中，当相机位姿以李代数表示时，误差项关于相机位姿导数的计算，容易发现，g2o提供了大量的顶点和边的类型，非常便于相机位姿估计问题。提供了运行时数值求导。