SLAM学习——后端（二）

1.投影模型和BA代价模型

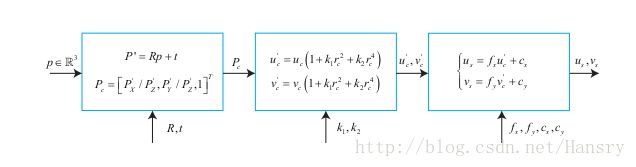
对于观测模型而言，我们可以简单的用以下的模型进行表示：z=h(x,y)

上图中，P点是世界坐标系的点，中间的畸变模块满足： r2c=u2c+v2c r c 2 = u c 2 + v c 2

把观测返程抽象出来，有：z=h(x,y) ，这里的x指代此时相机的位姿，即外参R,t，对应的李代数为 ξ ξ 。路边y即为三维点p，若观测数据(实际观测数据)为z，那么此次观测误差为： e=z−h(ξ,p) e = z − h ( ξ , p ) ，那么代价函数为：

12∑mi=1∑nj=1||eij||2=12∑mi=1∑nj=1||zij−h(ξi,pj)||2 1 2 ∑ i = 1 m ∑ j = 1 n | | e i j | | 2 = 1 2 ∑ i = 1 m ∑ j = 1 n | | z i j − h ( ξ i , p j ) | | 2

其中 zij z i j 为姿态i观察路标点j所产生的数据。

使用非线性优化来优化这个代价函数，当把所有的自变量定义成所有待优化的变量时，即：

x=[ξ1,⋯,ξm,ρ1,⋯,ρn] x = [ ξ 1 , ⋯ , ξ m , ρ 1 , ⋯ , ρ n ]

那么整个代价函数就可以变成：

12||f(x+Δx)||2≈12∑mi=1∑nj=1||eij+FijΔξi+EijΔρj||2 1 2 | | f ( x + Δ x ) | | 2 ≈ 1 2 ∑ i = 1 m ∑ j = 1 n | | e i j + F i j Δ ξ i + E i j Δ ρ j | | 2

其中 Fij F i j 表示整个代价函数在当前状态下对相机姿态的偏导数， Eij E i j 表示对路标点的偏导。

假如我们把所有的位姿都放到一块，把所有的路标点都放到一块，那么我们可以将代价函数转化成：

12||e+FΔxc+EΔxp|| 1 2 | | e + F Δ x c + E Δ x p | | (其中 Δxc Δ x c 表示位姿的集合， Δxp Δ x p 表示路标的集合)

这样一来，这里的雅克比矩阵E和F表示整体目标函数对整体变量的导数。这个雅克比矩阵将是个很大的矩阵，都是由每个误差项的导数“拼凑”起来。

对于非线性优化而言，核心的部分是求取增量方程： HΔx=g H Δ x = g

根据第六讲的内容，我们知道高斯牛顿法和列文伯格-马夸而特的主要差别在于H是取 JTJ J T J 还是 JTJ+λI J T J + λ I ，我们知道J=[F E]

以高斯牛顿法为例，则H矩阵为：H= JTJ J T J = [FTFETFFTEETE] [ F T F F T E E T F E T E ] (特征点复杂，整个矩阵庞大，计算量大，但是具有一定的特殊结构，可利用这个结构求解)

2.H矩阵的稀疏结构

H矩阵的稀疏结构引起的原因：对于一个误差项 eij e i j ，雅克比矩阵只对相应的位姿及其路标点有一定作用，但是对其他的误差项对应的位姿和路标偏导数为0。

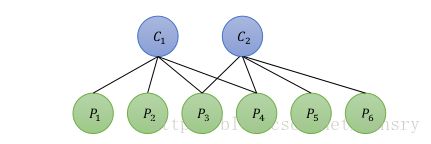
假设一个场景里面有2个相机位姿 (C1,C2) ( C 1 , C 2 ) 和6个路标 (P1,P2,P3,P4,P5,P6) ( P 1 , P 2 , P 3 , P 4 , P 5 , P 6 ) ，则可以形成点和边组成的示意图，如下图所示：

则场景下目标函数则有：

12(||e11||2+||e12||2+||e13||2+||e14||2+||e21||2+||e22||2+||e23||2+||e24||2) 1 2 ( | | e 11 | | 2 + | | e 12 | | 2 + | | e 13 | | 2 + | | e 14 | | 2 + | | e 21 | | 2 + | | e 22 | | 2 + | | e 23 | | 2 + | | e 24 | | 2 )

以 e11 e 11 为例，描述了在第一个位姿看到第一个观测点，与其他相机位姿和路标无关。令 J11 J 11 为 e11 e 11 所对应的雅克比矩阵，那么这个雅克比矩阵对其他相机位姿和其他路标点的偏导数为0。

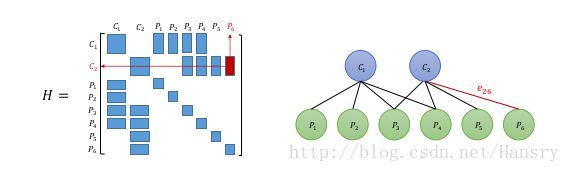
在接下来的表示方法中，我们都用阴影表示非0，用空白表示为0。那么，为了得到该目标函数的雅克比矩阵，我们可以将 Jij J i j 按照一定顺序列为向量，那么整体雅克比矩阵以及H矩阵如下：

对于上述J和H的结果，我们可以稍微用程序体验一下：

#include 
#include 
using namespace std;

int main(int argc, char **argv)
{
   Eigen::Matrix<double,8,8> matrix_1;
   matrix_1<<1,0,1,0,0,0,0,0,
             1,0,0,1,0,0,0,0,
             1,0,0,0,1,0,0,0,
             1,0,0,0,0,1,0,0,
             0,1,0,0,1,0,0,0,
             0,1,0,0,0,1,0,0,
             0,1,0,0,0,0,1,0,
             0,1,0,0,0,0,0,1;
   Eigen::Matrix<double,8,8> matrix_2;
   matrix_2=matrix_1.transpose();
   Eigen::Matrix<double,8,8> result_matrix=matrix_2*matrix_1;
   cout<return 0;
}

H矩阵的结果是：

4 0 1 1 1 1 0 0
0 4 0 0 1 1 1 1
1 0 1 0 0 0 0 0
1 0 0 1 0 0 0 0
1 1 0 0 2 0 0 0
1 1 0 0 0 2 0 0
0 1 0 0 0 0 1 0
0 1 0 0 0 0 0 1

对于上面的H矩阵来说，对角线为非0块，除对角线外的非零模块来说可以理解为俩个变量之间的存在联系或者称之为约束，如下图所示：

利用H矩阵的稀疏性，我们可以加速方程 HΔx=g H Δ x = g 的计算，我们可以把H矩阵分成以下模块：

这里与我们之前提到的方程 H=[FTFETFFTEETE] H = [ F T F F T E E T F E T E ] （F、E分别是整体代价函数对位姿、路标点的偏导数）

则对应的线性方程组 HΔx=g H Δ x = g 变为如下形式：

[BETEC][ΔxcΔxp]=[vw] [ B E E T C ] [ Δ x c Δ x p ] = [ v w ]

在上述式子中，B、C均为对角块矩阵，求逆会比一般矩阵容易得多，因此我们将上面等式的E给消掉，在等式左右俩边分别左乘： [I0−EC−1I] [ I − E C − 1 0 I ] ，得到下面公式：

[B−EC−1ETET0C][ΔxcΔxp]=[v−EC−1ww] [ B − E C − 1 E T 0 E T C ] [ Δ x c Δ x p ] = [ v − E C − 1 w w ]

方程组第一行编程和观测点无关的项，单独拿出来后可得：

[B−EC−1ET0]Δxc=v−EC−1w [ B − E C − 1 E T 0 ] Δ x c = v − E C − 1 w

这个线性方程的维度和B矩阵一样，我们的做法是先求出位姿 Δxc Δ x c ，然后再求出 Δxp Δ x p 。这个过程称为Marginalization

这样的好处在于，在消元过程中，由于C为对角阵，所以逆矩阵方便求得，在求得 Δxc Δ x c 之后，路标部分的增量方程由： Δxp=C−1(w−ETΔxc) Δ x p = C − 1 ( w − E T Δ x c )

因此整个过程的计算量主要在于： [B−EC−1ET0]Δxc=v−EC−1w [ B − E C − 1 E T 0 ] Δ x c = v − E C − 1 w ，将这个方程的系数设为S，同时，我们知道，S矩阵的非对角线上的非零矩阵块，表示了该处对应的俩个相机变量之间存在者共同观测的路标点，有时候称为共视。 反之，如果在该矩阵的非对角模块上为0，那么则俩个相机之间没有共同观测点。

关于S矩阵的稀疏性，是取决与实际观测结果的，我们无法提前预知。

为什么我们吧这一步称为边缘化呢？ 实际上我们把求 (Δxc,Δxp) ( Δ x c , Δ x p ) 转换成先求

3.鲁棒核函数

在前面BA中，我们用最小化误差项的二范数平方和作为目标函数。存在的问题是：如果当有一个匹配错误的边，形成的误差很大，那么回导致整个优化算法不准确。

这时候利用鲁棒核函数，保证每条边的误差不会大得掩盖其他边。方法：

将误差的而二范数替换成增长没那么快的函数，同时保证其光滑性（不然没法求导）。因为它们使得整个优化更稳健，因此称为鲁棒核函数。

最常用的鲁棒核函数Huber核： H(e)={12e2,|e|≤δδ(|e|−12δ),others H ( e ) = { 1 2 e 2 , | e | ≤ δ δ ( | e | − 1 2 δ ) , o t h e r s

当e大于一定阈值时，函数增长从二次形式变成了一次形式，降低增长速率。

4.位姿图

在上述中知道了带有相机和空间点的图优化称为BA，能够有效求解大规模的定位与建图问题。但是时间一多，效率就会下降了。

另外一种方法是，完全构建一个只有轨迹的图优化，而位姿节点之间的边，可以由俩个关键帧之间通过特征匹配之后得到的运动估计来给定初始值。一旦初始估计完成，我们就不再优化那些路标点的位置，而只是关心所有的相机位姿之间的联系了。通过这种方式，我们省去了大量的特征点优化的计算，只保留了关键帧的轨迹，从而构建了所谓的位姿图。

简单来说，就是利用特征点配对这种方式(ORB SLAM之类的)求出位姿，然后等位姿固定之后，不再优化路标点，只关心运动估计位姿。（这里只提供简单的思路）