机器学习 -- 线性回归（Linear Regression）原理及算法实现

---

借鉴至：LionKing数据科学专栏

1. 线性回归的原理

假设有一个数据集，希望通过一些特征 $x_1$,…,$x_p$预测目标变量 $y$.最简单的模型是假设目标变量 $y$ 是这些特征的某个线性组合：

$$y\approx a_0+a_1{x}_1+\cdot \cdot \cdot +a_p{x}_p$$

记第 $i$ 组观测为 $(x_1^{(i)},...,x_n^i,y^i)$ 。总共有 $n$ 组观测。

第 $i$ 组观测的预测值为 $y^{(i)}=a_0+a_1{x}_1^{(i)}+...+a_p{x}_p^{(i)}$

我们将 $a_0,a_1,.....,a_p$ 视为参数， 最小化均方误差（Mean Squared Error）：

$$L(a_0,a_1,.....,a_p)=\frac{1}{n}[(y^{(1)}-y^{(1)}{)}^2+...+(y^{(n)}-y^{(n)}{)}^2]$$

2. 算法

假设 $x_0=1,x_1,......,x_p$ 组成的数据矩阵 $X_{n\times (p+1)}$ 列满秩（full column rank)，即秩为 （p+1）。则 $X^{T}X$ 是秩为 （p+1）的方阵，因此可逆。并且最优的参数 $(a_0,a_1,......,a_p)$ 满足正规方程（normal equation）:

$$X^{T}X\left[\begin{array}{c}{a}_0\\ a_1\\ ...\\ a_p\end{array}\right]=X^{T}y$$

因为 $X^{T}X$ 可逆，可以通过求解该线性系统得到待求的参数。当 $p$ 过大时，求解线性系统的效率就会很低，因此我们转而使用 梯度下降（Gradient Descent） 近似地估计参数。

3. Python实现

Python中的 scikit-learn 包 可以进行线性回归模型的训练：scikit-learn线性回归模型文档

 print(__doc__)


    # Code source: Jaques Grobler
    # License: BSD 3 clause
    
    
    import matplotlib.pyplot as plt
    import numpy as np
    from sklearn import datasets, linear_model
    from sklearn.metrics import mean_squared_error, r2_score
    
    # Load the diabetes dataset
    diabetes = datasets.load_diabetes()
    
    
    # Use only one feature
    diabetes_X = diabetes.data[:, np.newaxis, 2]
    
    # Split the data into training/testing sets
    diabetes_X_train = diabetes_X[:-20]
    diabetes_X_test = diabetes_X[-20:]
    
    # Split the targets into training/testing sets
    diabetes_y_train = diabetes.target[:-20]
    diabetes_y_test = diabetes.target[-20:]
    
    # Create linear regression object
    regr = linear_model.LinearRegression()
    
    # Train the model using the training sets
    regr.fit(diabetes_X_train, diabetes_y_train)
    
    # Make predictions using the testing set
    diabetes_y_pred = regr.predict(diabetes_X_test)
    
    # The coefficients
    print('Coefficients: \n', regr.coef_)
    # The mean squared error
    print("Mean squared error: %.2f"
          % mean_squared_error(diabetes_y_test, diabetes_y_pred))
    # Explained variance score: 1 is perfect prediction
    print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
    
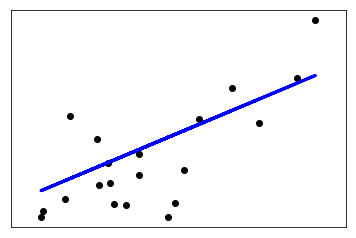
    # Plot outputs
    plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
    plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
    
    plt.xticks(())
    plt.yticks(())
    
    plt.show()
    

输出：
Automatically created module for IPython interactive environment
Coefficients:
[938.23786125]
Mean squared error: 2548.07
Variance score: 0.47

4. 共线性（Collinearity）

当数据矩阵 $X_{n\times (p+1)}$ 不是满秩时，正规方程中的 $X^{T}X$ 不可逆，任何满足正规方程的参数都能够最小化均方误差。满足要求的解有无限多个，因此得出的解容易过拟合（Overfiting）。这个问题又称为数据的共线性。
如果 $n⩽p$ ,则数据一定共线性。否则，数据很少精确地满足共线性。即使数据不是精确地满足共线性，也可能会非常接近列不满秩。此时 $X^{T}X$ 虽然可逆，但是数值求解其逆矩阵（Inverse Matrix）非常不稳定，这样得到的不稳定解也容易产生过拟合。

解决共线性的方法主要有两种。第一种是找出共线性的列并且删除其中一列直到数据列满秩。第二种是使用正则化（Regularization）。

5. 岭回归（Ridge Regression），Lasso回归和弹性网络（Elastic Net）回归

对于线性归回，正则化的两种是使用岭回归（Ridge Regression）或Lasso。
岭回归的思想是在原来的均方误差损失函数的基础上加上参数的 $l_2$范数平方作为惩罚项。新的损失函数是：

$$L_{\lambda }(a_0,a_1,...,a_p)=L(a_0,a_1,...,a_p)+\frac{\lambda }{n}[a_0^2+a_1^2+...+a_p^2]$$

类似原来的正规方程，新的方程为：

$$(X^{T}X+\lambda I_{p+1})\left[\begin{array}{c}{a}_0\\ a_1\\ ...\\ a_p\end{array}\right]=X^{T}y$$

由于 $X^{T}X$ 一定是半正定（Positive Semi-definite）的，只要 $\lambda >0,X^{T}X+\lambda I_{p+1}$ 的每一个特征值都不小于 $\lambda$,因此 $X^{T}X+\lambda I_{p+1}$ 是正定（Positive Definite）的，进而可逆。岭回归的解存在且唯一。

Lasso的思想是在均方损失误差的基础上加上参数的 $l_1$ 范数作为惩罚项。新的损失函数是：

$$L_{\lambda }(a_0,a_1,...,a_p)+\frac{\lambda }{n}[|a_0|+|a_1|+...+|a_p|]$$

Lasso的求解相对于岭回归复杂一些，主流的算法是 Least Angle Regression(LARS).
Lasso倾向于得出稀疏（Sparse)解，岭回归倾向于得出稠密（Dense）解。

弹性网络（Elastic Net）结合了两者，同时使用 $l_2$范数和 $l_1$范数作为惩罚项，其形式如下：

$$L_{\lambda }(a_0,a_1,...,a_p)=L(a_0,a_1,...,a_p)+\frac{\lambda }{n}(\tau {\Vert \beta \Vert }_2^2+(1-\tau ){\Vert \beta \Vert }_1)$$

其中，$0⩽\tau ⩽1$ 调节两种惩罚的比例，若 $\tau =0$ ，则弹性网络回归化为Lasso回归；若 $\tau =1$，则弹性网络回归化为岭回归。

弹性网络回归的好处是即保留了稀疏性，又可以把相关性高的变量同时找出来。

6. 均方误差的概率意义

线性回归采用最小化残差平方和主要有三个原因：第一，数学上残差平方和的解，在数据列满秩的前提下，存在且唯一；第二，平方和的解有显式数学解可以精确求得；第三，最小化残差平方和等价于正态（Gaussian）假设下的最大似然估计（Maximum Likelihood Estimation）。

对于第三点，假设数据来自 $y=X\beta +\epsilon$,其中 $\epsilon \sim N(0,{\sigma }^2)$。

给定数据 $(X^{(1)},y^{(1)}),.....,(X^{(n)},y^{(n)})$,第 $i$ 组数据的似然即 $y^{(i)}-X^{(i)}\beta$ 在正态分布中的概率密度：

$$L_i=\frac{1}{\sqrt{2\pi a}}exp[-\frac{(y^{(2)}-X^{(i)}\beta {)}^2}{2{\sigma }^2}]$$

总体的似然为 $L=L_1{L}_2...L_n$。最大化似然即最大化每个数据的对数似然（Log Likelihood）之和：

$$l=log{L}_1+...+log{L}_n$$

$$log{L}_i=-log(\sqrt{2\pi }\sigma )-\frac{1}{2{\sigma }^2}(y^{(i)}-X^{(i)}\beta {)}^2$$

$$l=-nlog(\sqrt{2\pi }\sigma )-\frac{1}{2{\sigma }^2}[(y^{(1)}-y^{(1)}{)}^2+...+(y^{(n)}-y^{(n)}{)}^2]$$

因此最大化 $l$ 等价最小化 $[(y^{(1)}-y^{(1)}{)}^2+...+(y^{(n)}-y^{(n)}{)}^2]$, 即残差平方和。

7. 岭回归的概率意义

岭回归从概率意义上可以看作在数据服从高斯噪声假设下，参数的先验分布（Prior Distribution）为以 0 为中心的正态分布。
若假设参数 $\beta$ 服从先验分布 $N(0,{\tau }^2{I}_{p+1})$,则 $\beta$ 的先验概率为：

$$prior(\beta )=Cexp-\frac{{\Vert \beta \Vert }_2^2}{2{\tau }^2}$$

其中 $C$ 为只与 $p$ 和 $\tau$ 有关的常数。
根据贝叶斯定理（Bayes’ Theorem），数据的后验似然（Posterior Likelihood）与先验和 $L$ 的乘积成正比。

$$posterior(\beta ;X,y)\propto prior(\beta )L$$

$$log(posterior(\beta ;X,y))=C-\frac{1}{2{\tau }^2}{\Vert \beta \Vert }_2^2-\frac{1}{2{\sigma }^2}[(y^{(1)}-y^{(1)}{)}^2+...+(y^{(n)}-y^{(n)}{)}^2]$$

最大化后验似然等价于最小化：

$$[(y^{(1)}-y^{(1)}{)}^2+...+(y^{(n)}-y^{(n)}{)}^2]+\frac{{\sigma }^2}{{\tau }^2}{\Vert \beta \Vert }_2^2$$

取 $\lambda =\frac{{\sigma }^2}{{\tau }^2}$，最大化后验似然等价于岭回归的损失函数。

类似地，Lasso 可以视作给参数一个拉普拉斯分布（Laplace Distribution）作为先验。

8. 常见的面试问题

Q:为什么需要正则化？

Q:为什么 $l_1$ 更容易给出稀疏解（Sparse Solution）？

Q:$R^2$ 是什么？应当如何计算？

Q:共线性应该如何检测？

---