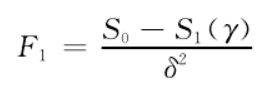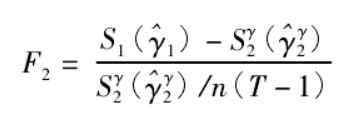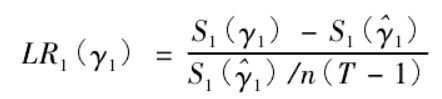Stata软件做门槛回归模型(汉森个人主页上的代码)
结合自身在stata软件实际操作中的经验,做出门槛回归模型的小结如下:
注:本人采用的是Hansen个人主页上的代码完成的,具体代码请在网上搜索BruceHansen的个人主页(门槛回归创始人)-左下角的Programs and Data--Organized by Subject--Threshold Models--STATA Programs
1、门槛变量的选择。门槛变量的选择可由理论模型外生决定,汉森指出,由于门槛回归方法是通过对门槛变量进行排序后进行模型估计的,如果门槛变量含有较强的时间趋势,就会将这种趋势带入模型中,趋势的存在将改变突变点似然分布检验,更重要的是,在这种情况下,置信区间无法构建,使得问题无法研究,因此本文在选取门槛变量时尽量避免选择带有趋势的绝对指标,而选择相对指标。
2、显著性检验。门槛回归模型的实质是利用门槛值将样本分为两组,只有当两组样本的估计参数显著不同时,才使用门槛回归模型,否则说明不存在门槛,使用线性模型就可以了,因此必须对模型进行显著性检验。
(1)门槛效应的存在性检验:单一门槛存在性检验。进行显著性检验的方法是汉森提出的LM(lagrange multiplier)检验,原假设为:
如果零假设H0被拒绝,则表示模型存在机制转换(即存在门槛);反之,则表示不存在门槛。但是该H0假设表示不存在门槛,这将导致门槛参数无法识别,此时检验统计量的大样本分布将是受到干扰参数影响的“非标准非相似分布”(non-standard non-similar),而不是“卡方分布”,那么就无法使用模拟的方法得到分布的临界值。汉森为了解决这个问题,利用统计量本身的大样本分布函数进行转换,并使用“自助抽样法”(bootstrap)进行计算,得到大样本的渐进p值。如果该p值统计量的大样本分布为均匀分布,则零假设成立。在对零假设进行统计检验时,可以利用LM统计量构造似然比统计量,其公式为:
式中,S0为在零假设(即无门槛值)下的残差平方和加总;S1为存在门槛效应下的残差平方和加总。如果拒绝了LM检验,则表示模型至少存在一个门槛值,此时要继续进行两个门槛值的检验。
(2)门槛效应的存在性检验:双重门槛的存在性检验(同上)
原假设为不存在门槛效应: H0∶ β1= β2= β3; 相应的备择假设?为 H1∶ β1≠β2(表示至少存在一个门槛)。我们采用自举抽样法( Bootstrap) 模拟似然比检验的渐进分布。
似然比检验基于如下统计量:
其中,S0为假设不存在门槛效应时β估计相应的残差平方和,S(^γ1)为存在单一门槛效应时β估计相应的残差平方和。n为样本国家个数,T为时间跨度。在重复多次自举抽样计算后,得到原假设H0下F1统计量的渐进p值,如果p值小于临界值(1%、5%或10%),那么就拒绝原假设。
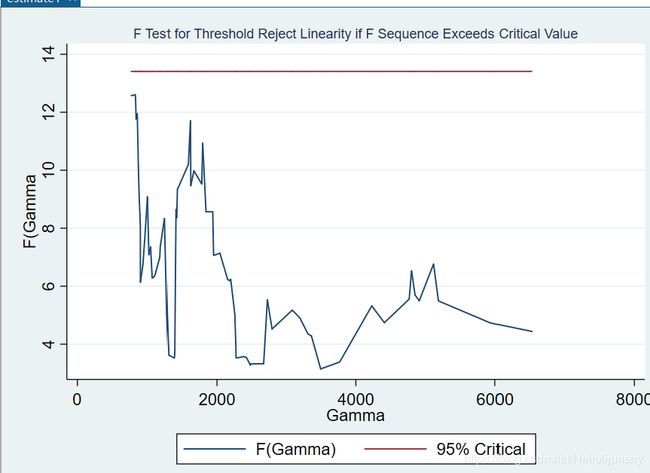
【例子】:汉森thresholdtest运行结果:F值(LM检验值)为12.6,对于P值为0.078.
thresholdtest运行结果中的P值为0.0788,所以存在一个门槛值,再运行thresholdreg得到具体门槛值。然后再在门槛值左右两部分分别做thresholdtest和thresholdreg,比较左右部分的thresholdreg结果里的SSE(残差平方和),哪个残差平方和小,对应的门槛值就是第二个门槛值。反过来,再依据第二个门槛值划分左右两部分,再在门槛值左右两部分分别做thresholdtest和thresholdreg,比较左右部分的thresholdreg结果里的SSE(残差平方和),哪个残差平方和小,对应的门槛值就是第一个门槛值。这样第一、二个门槛值就确定了,各自的回归方程也确定了。
结果说明在10%显著性水平下,存在门槛值,且至少存在一个门槛值。
(3)确定门槛值的个数。
在存在门槛效应的基础上,再确定门槛值的个数。以双门槛模型为例。由于双重门槛模型可能存在两个也可能存在一个门槛,所以需要对门槛的个数进行检验。原假设为存在单一门槛: H0: β1= β2≠ β3(数字顺序可调换,表示仅存在1个门槛值); 相应的备择假设为 H1: β1≠ β2≠ β3(至少存在2个门槛值)。该检验基于如下统计量:
如果 F2大于临界值,那么拒绝仅存在一个门槛的假设。如果不只存在单一门槛,还
需对模型进一步检验以确定是双重门槛、三重门槛、四重门槛…或是 n 重门槛。
(4)确定门槛值的个数的理论过程
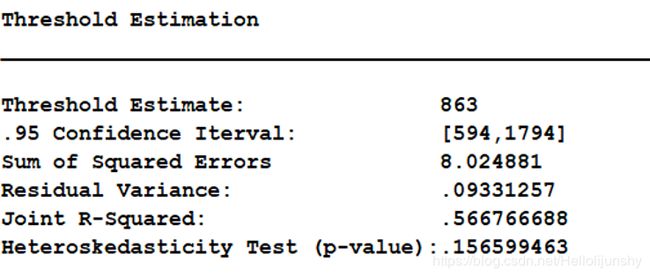
就是Sum of Squared Iterval最小时的Threshold Estimate值
3、门槛效应的真实性检验
显著性检验只能检验样本是否存在门槛值,如果存在门槛值,但是门槛估计值γ与实际门槛值γ0是否一致却无法确定。这是因为存在着干扰参数,它使得渐进分布呈高度非标准分布。因此汉森提出使用最大似然估计法求得统计量的渐进分布,来检验门槛估计值γ与门槛实际值γ0是否具有一致性。门槛值检验的原假设为:H0∶γ=γ0 ,其似然比统计量为式:
在确定了门槛值之后,还要构造 γ 的置信区间对“门槛效应”进行真实性检验。对于
单一门槛估计值的渐进分布特征,设 γ 为真实值,^γ 为 γ 的一致估计量,它的分布是高
度非标准分布,故利用似然比统计量构造出“非拒绝域”。对于单门槛模型,原假设为 H0:
^γ1= γ1,似然比统计量为:
对于双门槛估计值的渐进分布特征,记 ( γ1,γ2) 为真实值,( ^γ1,^γ2) 为 ( γ1,γ2)的一致估计量,原假设为 H0: ( ^γ1,^γ2) = ( γ1,γ2) ,似然比统计量为:
门槛回归结果中,系数的t值自己算,t=系数估计值/st error,然后再根据样本数n和变量数q查t值表得到在1%、5%和10%显著性水平下的临界值。拿计算出的t值与临界值比较。
STATA15软件中命令threshold默认为时间序列,并不适用横截面与面板数据,故首先需要tsset数据,才能使用threshold命令。所以如果对横截面数据进行门槛回归或进行深入的统计推断,则建议使用门槛回归创始人BruceHansen的个人网页提供的非官方Stata命令(即thresholdreg和thresholdtest命令)
网页:https://www.ssc.wisc.edu/~bhansen/progs/progs_threshold.html
如果使用面板数据进行门槛回归,则建议使用南开大学王群勇教授的非官方Stata命令xthreg(Wang,2015),在stata中可输入命令finditxthreg来搜索下载
结尾附上汉森程序代码和含义
在汉森STATA程序文件中有如下5个文件:
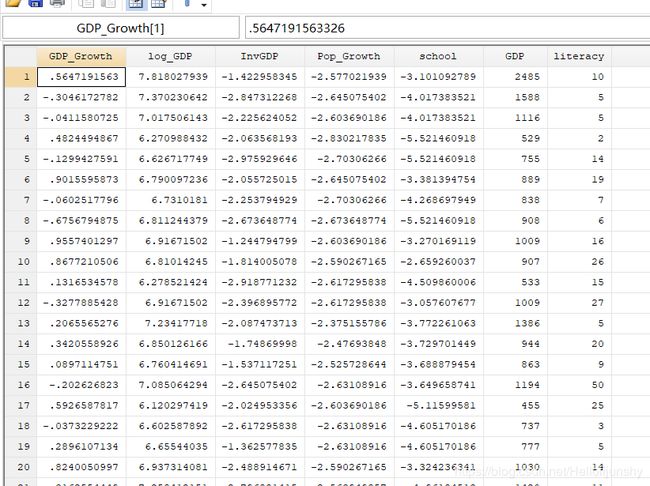
原始数据是如下这种形式:
在实际操作中,先运行thresholdtest.ado和thresholdreg.ado文件,再分别运行
thresholdtest GDP_Growth log_GDP InvGDP Pop_Growth school, q(GDP) trim_per(0.15) rep(5000)
来检验门槛效应是否存在;
thresholdreg GDP_Growth log_GDP InvGDP Pop_Growth school, q(GDP) h(1)
来做门槛回归。