Octave教程五:控制语句if/while/for以及函数的定义和使用
Octave教程五:控制语句if/while/for以及函数的定义和使用
在这篇文章中,我将告诉你该怎样为你的Octave程序写控制语句,诸如if/while/for这些语句,以及如何定义和使用方程。
>> for i = 1:10,
> v(i) = 2^i;
> end;
>> v
v =
2 4 8 16 32 64 128 256 512 1024
>> indices = 1:10;
>> indices
indices =
1 2 3 4 5 6 7 8 9 10
>> for i = indices,
> disp(i);
> end;
1
2
3
4
5
6
7
8
9
10
>> a = 1:10;
>> a
a =
1 2 3 4 5 6 7 8 9 10
>> v
v =
2 4 8 16 32 64 128 256 512 1024
>> V
V =
0
0
0
0
0
0
0
0
0
0
>> v = v'
v =
2
4
8
16
32
64
128
256
512
1024
>> i = 1;
>> while i <= 5,
> v(i) = 100;
> i = i + 1;
> end;
>> v
v =
100
100
100
100
100
64
128
256
512
1024
>> i = 1;
>> while true,
> v(i) = 999;
> i ++;
> if i == 6,
> break;
> end;
> end;
>> v
v =
999
999
999
999
999
64
128
256
512
1024
>> v(1)
ans = 999
>> v(1) = 2;
>> if v(1) == 1,
> disp('the value is one');
> elseif v(1) == 2,
> disp('the value is two');
> else
> disp('the value is not one or two');
> end;
the value is two
>>现在我们来说如何在Octave里定义函数:
这个文件只有三行,第一行写着function y = squareThisNumber(x),这就告诉octave,我想返回一个值,并且这个返回的值,我想放在变量y中;另外,它告诉了octave这个函数有一个参数,就是参数x,还有定义的函数体,也就是y等于x的平方。
现在让我们尝试调用这个函数。
>> squareThisNumber(5)
error: 'squareThisNumber' undefined near line 1 column 1
>>出错:这个函数未被定义
这是因为octave不知道在哪里找这个函数
>> pwd
ans = C:\fakepath\octave4
>> cd 'D:\soft\Octave\user'
>> squareThisNumber(5)
parse error near line 1 of file D:\soft\Octave\user\squareThisNumber.m
syntax error
>>>
^出错,修改SquareThisNumber.m文件,如下所示:
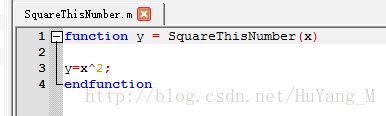
此时,程序便可正常运行:
>> SquareThisNumber(5)
ans = 25
>> SquareThisNumber(5)
ans = 25
>> SquareThisNumber(8)
ans = 64
>>>> % Octave search path (advanced/optional)
>> addpath ('C:\fakepath\octave4')
>> SquareThisNumber(5)
ans = 25
>> pwd
ans = D:\soft\Octave\user
>> addpath ('D:\soft\Octave\user')
>> cd 'C:\'
>> SquareThisNumber(5)
ans = 25
>> cd
>> pwd
ans = C:\Users\huyang
>>我们再来看另外一种情况:
我们在D:/soft/Octave/user目录下创建squareAddCubeThisNumber.m文件,内容为:

>>
>> [a,b] = squareAddCubeThisNumber(5)
a = 25
b = 125
>>>> [a,b] = squareAddCubeThisNumber(5);
>> a
a = 25
>> b
b = 125
>>接下来,我想设计一个复杂一点的函数:
比方说,我有一个数据集,像这样,数据点为[1,1],[2,2],[3,3]
我想做的事是定义一个octave函数来计算代价函数J(θ),就是计算不同θ值所对应的代价函数值J。
首先让我们把数据放在octave里,如下所示:
>> X = [1 1;1 2;1 3]
X =
1 1
1 2
1 3
>> Y = [1;2;3]
Y =
1
2
3
>> theta = [0;1];
>>接下来,我定义一个costFunctionJ.m函数,如下图所示:
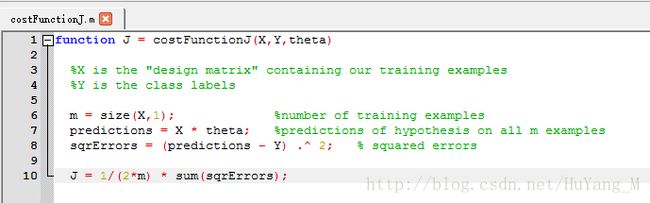
源代码如下:
function J = costFunctionJ(X,Y,theta)
%X is the "design matrix" containing our training examples
%Y is the class labels
m = size(X,1); %number of training examples
predictions = X * theta; %predictions of hypothesis on all m examples
sqrErrors = (predictions - Y) .^ 2; % squared errors
J = 1/(2*m) * sum(sqrErrors);接下来,我们写如下代码:
>> P = Y .^ 2
P =
1
4
9
>> sum(P)
ans = 14
>> J = costFunctionJ(X,Y,theta)
J = 0
>>屏幕输出J = 0,这是因为,如果我的数据集x为[1;2;3],y也为[1;2;3],然后设置θ0为0,θ1 = 1,这就恰好是45°的斜线,这条线是可以完美拟合我的数据集的;而相反地,如果我设置θ = [0;0],那么这个假设所计算出的J就如下图所示:
>>
>> theta = [0;0]
theta =
0
0
>> J = costFunctionJ(X,Y,theta)
J = 2.3333
>>>>
>> (1^2 + 2^2 + 3^2) / (2 * 3)
ans = 2.3333
>>