走进数据结构和算法（c++版）（9）——图

图

  前面我们已经介绍了一对一和一对多的数据结构，现在我们就来了解一下多对多的数据结构。

图( Graph )是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为: G (V， E )，其中， G 表示一个图， V 是图G 中顶点的集合， E 是图G 中边的集合。

              
$$图1$$
###术语总结

  图的术语很多：
  图按照有无方向分为无向图和有向图。无向图由顶点和边构成，有向图由顶点和弧何成。弧有弧尾和弧头之分。
  图按照边或弧的多少分稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图，有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
  图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分为入度和出度。
  图上的边或弧上带权则称为网。
  图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环， 当中不重复叫简单路径。若任意两顶点都是连通的，则图就是连通图，有向则称强连通图。图中有子图， 若子图极大连通则就是连通分量， 有向的则称强连通分量。
  无向图中连通且$n $个顶点$n-1$条边叫生成树。有向图中一顶点入度为0其余顶点入度为1 的叫有向树。一个有向图由若干棵有向树构成生成森林。

###图的存储结构

  图的结构比较复杂，不可能用简单的顺序存储结构来表示。现在我们介绍几种常用的图的存储结构。

####邻接矩阵

  考虑到图由顶点和边组成，所以我们可以将图分开分别储存。这就是邻接矩阵的思路。

图的邻接矩阵( Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维
数组存储图中顶点信息，一个二维数组（称为邻接矩阵)存储图中的边或弧的信息。

  其中邻接矩阵定义如下：
$$arc[i][j]=\{\begin{array}{c}1,(v_i,v_j)ϵE或<v_i,v_j>ϵE\\ 0,其他\end{array}$$

  对于网图邻接矩阵定义如下：
$$arc[i][j]=\{\begin{array}{c}{W}_{ij},(v_i,v_j)ϵE或<v_i,v_j>ϵE\\ 0,i=j\\ \infty ,其他\end{array}$$

  其中$W_{ij}$为相对应边的权值。
  相关代码如下：

#include 
#include 
using namespace std;
#define INFINITY 65535
class Graph
{
public:
	Graph();
	~Graph();
	void CreateGraph();//创建图
private:
	vector vexs; //顶点表
	vector>arc;//邻接矩阵
	int numVertexes, numEdges;
};

  以无向网图为例的创建代码如下：

void Graph::CreateGraph()
{
	cout << "输入顶点数和边数:" << endl;
	cin >> numVertexes >> numEdges;
	cout << "输入顶点：" << endl;
	int i, j,w;
	char ch;
	for (i = 0; i < numVertexes; i++)
	{
		cin >> ch;
		vexs.push_back(ch);
	}
	arc.resize(numVertexes, vector(numVertexes));
	for ( i = 0; i < numVertexes; i++) //初始化邻接矩阵
		for (j = 0; j < numVertexes; j++)
		{
			if (i!=j)arc[i][j] = INFINITY;
			else arc[i][j] = 0;
		}
			
	cout << "输入边( vi ，vj)上的下标i,下标j,和权w :" << endl;
	for (int k = 0; k < numEdges; k++)
	{
		cin >> i >> j >> w;
		arc[i][j]=arc[j][i]= w;
	}
}

####邻接表

  对于边数相对顶点较少的图，邻接矩阵存在对存储空间的极大浪费的。这时候可以选择采用邻接表 ，它是数组与链表相结合的存储方法。类似树存储结构的孩子表示法。

1. .图中顶点用一个一维数组存储，另外，对于顶点数组中，每个数据元
   素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。
2. 图中每个顶点的所有邻接点构成一个线性表。

#include
#define INFINITY 65535
using namespace std;
 struct EdgeNode//边表结点
{
	int adjvex;//顶点下标
	int weight;//权值
	EdgeNode *next;//下一个结点
};
 struct VertexNode//顶点表结点
 {
	 char vert;//顶点信息
	 EdgeNode* firstedge;//边表头指针
 };
class GraphAdjList
{
public:
	GraphAdjList();
	~GraphAdjList();
	void CreateALGraph();//构建无向网图
private:
	vector adjList;
	int numVertexes, numEdges;//顶点数、边数
};

  以无向网图为例的创建代码如下：

void GraphAdjList::CreateALGraph()//构建无向网图
{
	int i,j,w;
	cout << "输入顶点数和边数:" << endl;
	cin >> numVertexes >> numEdges;
	cout << "输入顶点：" << endl;
	VertexNode vert;
	for (int k = 0; k < numVertexes; k++)
	{
		cin >> vert.vert;
		vert.firstedge = NULL;
		adjList.push_back(vert);
	}
	cout << "输入边( vi ，vj)上的下标i,下标j,和权w :" << endl;
	for (int k = 0; k < numEdges; k++)
	{
		cin >> i >> j >> w;
		EdgeNode *p = new EdgeNode;
		p->adjvex = j;
		p->weight = w;
		p->next = adjList[i].firstedge;
		adjList[i].firstedge=p;
	}

}

###图的遍历

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历(Traversing Graph )

####深度优先遍历

  深度优先遍历( Depth_First_Search ) 也有称为深度优先搜索，简称为DFS。
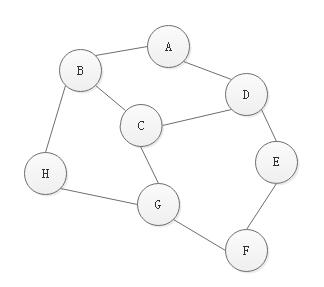
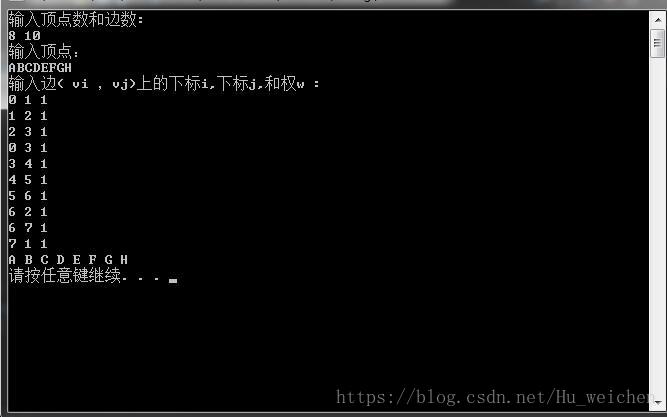
  它从图中某个顶点v 出发，访问此顶点，然后从v 的未被访问的邻接点出发深度优先遍历图，直至图中所有和v 有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。图1中图的邻接矩阵的深度优先遍历，代码如下：

#include 
#include 
using namespace std;
#define INFINITY 65535
class Graph
{
public:
	Graph();
	~Graph();
	void CreateGraph();//创建图
	void DFSTraverse();//深度遍历操作
	
private:
	void DFS(int i);//深度遍历递归数组
	vector vexs; //顶点表
	vector>arc;//邻接矩阵
	vectorvisited;//访问标志数组
	int numVertexes, numEdges;
};

  代码具体实现：

#include "Graph.h"


Graph::Graph()
{
}


Graph::~Graph()
{
}
void Graph::CreateGraph()
{
	cout << "输入顶点数和边数:" << endl;
	cin >> numVertexes >> numEdges;
	cout << "输入顶点：" << endl;
	int i, j,w;
	char ch;
	for (i = 0; i < numVertexes; i++)
	{
		cin >> ch;
		vexs.push_back(ch);
	}
	arc.resize(numVertexes, vector(numVertexes));
	for ( i = 0; i < numVertexes; i++) //初始化邻接矩阵
		for (j = 0; j < numVertexes; j++)
		{
			if (i!=j)arc[i][j] = INFINITY;
			else arc[i][j] = 0;
		}
			
	cout << "输入边( vi ，vj)上的下标i,下标j,和权w :" << endl;
	for (int k = 0; k < numEdges; k++)
	{
		cin >> i >> j >> w;
		arc[i][j]=arc[j][i]= w;
	}
}
void Graph::DFSTraverse()//深度遍历操作
{
	for (int i = 0; i < numVertexes; i++)
		visited.push_back(false);
	for (int i = 0; i < numVertexes; i++)
		if (!visited[i])
			DFS(i);
	cout << endl;
}
void  Graph::DFS(int i)//深度遍历递归数组
{
	visited[i] = true;
	cout << vexs[i] << " ";
	for (int j = 0; j < numVertexes; j++)
		if ((arc[i][j] != 0 && arc[i][j] != INFINITY) && !visited[j])
			DFS(j);
}

#include 
#include "Graph.h"

using namespace std;

int main()
{
	Graph G;
	G.CreateGraph();
	G.DFSTraverse();
	system("pause");
	return 0;
}

  VS上运行结果如下：

####广度优先遍历

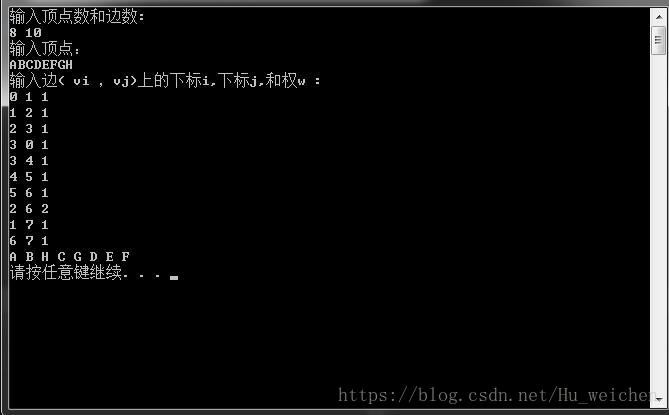
  广度优先遍历( Breadth_First_Search) ，又称为广度优先搜索，简称BFS。如果说图的深度优先遍历类似树的前序遍历， 那么图的广度优先遍历就类似于树的层序遍历了。图1中图的邻接表的广度优先遍历代码如下：

#include
#define INFINITY 65535
using namespace std;
 struct EdgeNode//边表结点
{
	int adjvex;//顶点下标
	int weight;//权值
	EdgeNode *next;//下一个结点
};
 struct VertexNode//顶点表结点
 {
	 char vert;//顶点信息
	 EdgeNode* firstedge;//边表头指针
 };
class GraphAdjList
{
public:
	GraphAdjList();
	~GraphAdjList();
	void CreateALGraph();//构建无向网图
	void BFSTraverse();//广度历遍算法
private:
	vector adjList;
	vector visited;//访问标志数组
	int numVertexes, numEdges;//顶点数、边数
};

  具体操作代码如下：

#include "GraphAdjList.h"
#include
#include
using namespace std;

GraphAdjList::GraphAdjList()
{
}


GraphAdjList::~GraphAdjList()
{
}

void GraphAdjList::CreateALGraph()//构建无向网图
{
	int i,j,w;
	cout << "输入顶点数和边数:" << endl;
	cin >> numVertexes >> numEdges;
	cout << "输入顶点：" << endl;
	VertexNode vert;
	for (int k = 0; k < numVertexes; k++)
	{
		cin >> vert.vert;
		vert.firstedge = NULL;
		adjList.push_back(vert);
	}
	cout << "输入边( vi ，vj)上的下标i,下标j,和权w :" << endl;
	for (int k = 0; k < numEdges; k++)
	{
		cin >> i >> j >> w;
		EdgeNode *p = new EdgeNode;
		p->adjvex = j;
		p->weight = w;
		p->next = adjList[i].firstedge;
		adjList[i].firstedge=p;
	}

}

void GraphAdjList::BFSTraverse()//广度历遍算法
{
	for (int i = 0; i < numVertexes; i++)
		visited.push_back(false);
	queue Q;
	EdgeNode* p;
	for (int i = 0; i < numVertexes; i++)
	{
		if (!visited[i])
		{
			visited[i] = true;
			cout << adjList[i].vert << " ";
			Q.push(i);
			while (!Q.empty())
			{
				i = Q.front();
				Q.pop();
				p = adjList[i].firstedge;
				while (p)
				{
					if (!visited[p->adjvex])
					{
						visited[p->adjvex] = true;
						cout << adjList[p->adjvex].vert << " ";
						Q.push(p->adjvex);
					}
					p = p->next;
				}
			}
		}
	}
	cout << endl;
}

#include
#include "GraphAdjList.h"

using namespace std;

int main()
{
	GraphAdjList G;
	G.CreateALGraph();
	G.BFSTraverse();
	system("pause");
	return 0;
}

  VS上运行结果如下：