JZOJ-senior-5963. 【NOIP2018提高组D1T3】赛道修建

Time Limits: 1000 ms Memory Limits: 524288 KB

Description

C城将要举办一系列的赛车比赛。在比赛前，需要在城内修建m条赛道。
C城一共有n个路口，这些路口编号为1,2,…,n ，有n-1 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第i条道路连接的两个路口编号为ai 和bi ，该道路的长度为li 。借助这n-1 条道路，从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路e1,e2,…,ek ，满足可以从某个路口出发，依次经过道路 e1,e2,…,ek（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的m条赛道中长度最小的赛道长度最大（即m条赛道中最短赛道的长度尽可能大）。

Input

输入文件名为track.in。
输入文件第一行包含两个由空格分隔的正整数 n,m，分别表示路口数及需要修建的赛道数。
接下来n-1 行，第i行包含三个正整数ai,bi,li ，表示第i条适合于修建赛道的道路连接的两个路口编号及道路长度。保证任意两个路口均可通过这n-1条道路相互到达。每行中相邻两数之间均由一个空格分隔。

Output

输出文件名为track.out。
输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

Sample Input

输入1：
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7

输入2：
9 3
1 2 6
2 3 3
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4

Sample Output

输出1：
31

输出2：
15

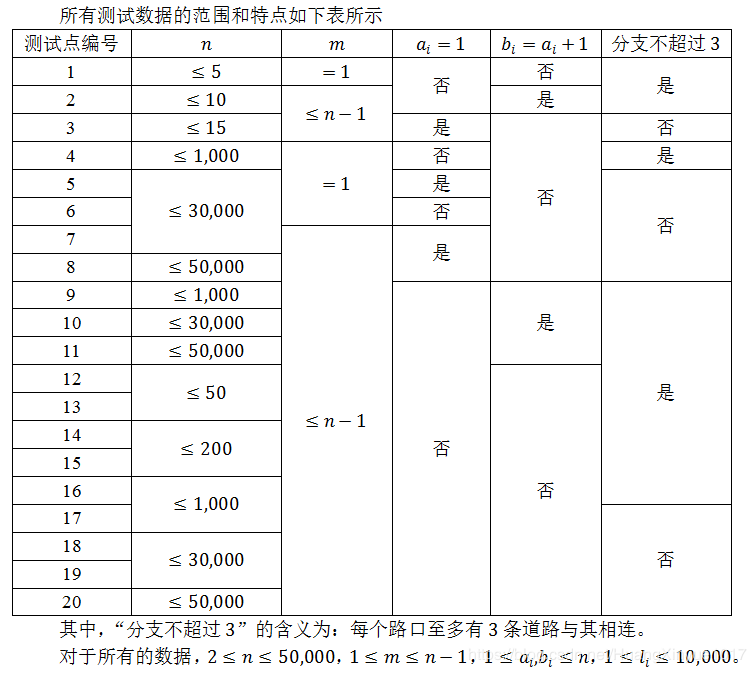
Data Constraint

Hint

【输入输出样例1说明】
所有路口及适合于修建赛道的道路如下图所示：

道路旁括号内的数字表示道路的编号，非括号内的数字表示道路长度。
需要修建1条赛道。可以修建经过第3,1,2,6条道路的赛道（从路口4到路口7），则该赛道的长度为9+10+5+7=31 ，为所有方案中的最大值。

【输入输出样例2说明】
所有路口及适合于修建赛道的道路如下图所示：

需要修建3条赛道。可以修建如下3条赛道：

1. 经过第1,6条道路的赛道（从路口1到路口7），长度为6+9=15 ；
2. 经过第5,2,3,8条道路的赛道（从路口6到路口9），长度为4+3+5+4=16 ；
3. 经过第7,4条道路的赛道（从路口8到路口5），长度为7+10=17。
   长度最小的赛道长度为15 ，为所有方案中的最大值。

Solution

最小长度最大，考虑二分+判定
考虑以 $x$ 为根的子树，最优解中一部分链在子树的内部，还有可能是一条经过 $x$ 往外延伸的链
可证明一定存在一个最优解使完全在子树内部的链尽可能多，否则可以调整子树内部的方案，不会使答案变差
如果有两种方案使得子树内部的链一样多，我们肯定希望使剩下可以往上扩展的链尽可能长
$sum[x]$ 表示在 $x$ 子树内合法的路径最多有多少条，$mx[x]$ 表示 $x$ 子树内在最多路径情况下往外延伸的链的最大长度
考虑用这两个值进行转移
首先，若 $mx[x]>=mid$ 肯定是不划算的，因为可以直接切出一条链
其次，对于每个儿子 $y$ ，它提供 $l[y]=mx[y]+len(x,y)$ 的可拼接链长以及 $sum[y]$ 的贡献
考虑对答案产生新贡献的两种情况
1.$l[y]>=mid$ 则 $sum[x]+1$
2.$l[y1]+l[y2]>=mid$ 的两条链拼接起来形成答案，$sum[x]+1$
这里的选择可以用multiset维护，注意一下细节

Code

#pragma GCC optimize(2)
#pragma G++ optimize(2)

#include
#include
#include
#include
#include

#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fd(i,a,b) for(int i=a;i>=b;--i)
#define ll long long

using namespace std;

const int N=5e4+5;
int n,m,num;
int a[N],mx[N],sum[N],last[N];
ll l=0,r=0,mid,ans=0;
struct edge{int to,next,l;}e[2*N];
multiset<int> S;
multiset<int>::iterator it,i1,i2;

inline void read(int &n)
{
	int x=0,w=0; char ch=0;
	while(!isdigit(ch)) w|=ch=='-',ch=getchar();
	while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	n=w?-x:x;
}

void link(int x,int y,int z)
{
	e[++num]=(edge){y,last[x],z},last[x]=num;
}

void dfs(int x,int fa)
{
	for(int w=last[x];w;w=e[w].next)
	{
		int y=e[w].to;
		if(y==fa) continue;
		dfs(y,x);
	}
	S.clear();
	int tot=0,cnt=0;
	for(int w=last[x];w;w=e[w].next)
	{
		int y=e[w].to;
		if(y==fa) continue;
		tot+=sum[y];
		int len=mx[y]+e[w].l;
		if(len>=mid) {++tot; continue;}
		S.insert(len);
		a[++cnt]=len;
	}
	sort(a+1,a+1+cnt);
	fd(i,cnt,1)
	{
		i1=S.find(a[i]);
		if(i1==S.end()) break;
		i2=S.lower_bound(mid-a[i]);
		if(i2==S.end()) break;
		if(i1==i2)
		{
			++i2;
			if(i2==S.end()) break;
		}
		S.erase(i1),S.erase(i2),++tot;
	}
	int tmp=0;
	if(!S.empty()) it=S.end(),it--,tmp=*it;
	sum[x]=tot,mx[x]=tmp;
}

int check()
{
	memset(mx,0,sizeof(mx));
	memset(sum,0,sizeof(sum));
	dfs(1,0);
	if(sum[1]>=m) return 1;
	return 0;
}

int main()
{
	freopen("track.in","r",stdin);
	freopen("track.out","w",stdout);
	read(n),read(m);
	fo(i,1,n-1)
	{
		int x,y,z;
		read(x),read(y),read(z);
		link(x,y,z),link(y,x,z);
		r+=z;
	}
	while(l<=r)
	{
		mid=(l+r)>>1;
		if(check()) l=mid+1,ans=max(ans,mid);
			else r=mid-1;
	}
	printf("%d",ans);
}