图像填充方法概述

总说

这里主要讲解Inpainting的主要发展历程。从2001年到2014年的图像填充方法概述。
1. ImageInpainting（00年）
2. Simultaneous Structure and Texture Image Inpainting
3. Object Removal by Exemplar-Based Inpainting
4. Shift-Map Image Editing
5. PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing
6. The Generalized PatchMatch Correspondence Algorithm
7. Image Completion Approaches Using the Statistics of Similar Patches
8. Image Inpainting (14年总结性的inpainting文章）

TODO

暂时不写第八篇了，有点累。以后再写吧。。

Image Inpainting(00年)

简单来说，该文章提出Inpainting的方法就是从已知区域往未知区域，逐步向内填充。
填充的公式如下：

In+1(i,j)=In(i,j)+ΔtInt(i,j),∀(i,j)∈Ω

而 Int(i,j) 则通过以下公式计算：

Int(i,j)=δLn−→−(i,j)⋅Nn−→−(i,j)

慢慢缕缕：未知区域定义为 Ω , 已知区域是 Ω¯¯¯ 。 In(i,j) 表示 (i,j) 坐标的点在第 n 次迭代时的值。 Δt 表示步长。所以 Int(i,j) 自然是 (i,j) 点在第 n 次时需要传播（propagate）总信息量。那么这个总信息量的定义是和 δLn−→− 以及 Nn−→−(i,j) 有关的。
δLn−→−(i,j) ： 这个表示(i,j)点的信息的变化量。
Nn−→−(i,j) :表示一个方向，后面说明这个方向。

L→(i,j) 应该是图像的光滑估计算子。论文中这里取拉普拉斯算子。
Ln−→(i,j)=Inxx(i,j)+Inyy(i,j) , 那么 Nn−→−(i,j)

如何定义 N→(i,j)

如何定义呢？一个简单的想法是，定义成垂直于边界 δΩ 的signed distance。比如是这样的：

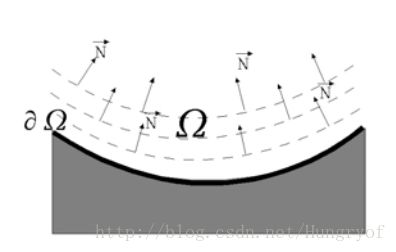
对于每个点（在 Ω 内）， N 方向应该垂直于一个收缩的 ∂Ω 。但是如果这样设定 N 的话，可能会出现下面这种填充：

这样的设定 N ，会使得右边的填充出来的边缘直接变化了（本开应该要继续斜向上的，但是这里直接边缘垂直向上了）。因此不能直接定义 N 垂直与 ∂Ω , 论文中采用等照度线的方向（这里直接认为垂直于梯度的方向即为等照度线方向)。
定义：
Nn−→−(i,j):=∇⊥In(i,j) ，其中 ∇⊥In(i,j) 是垂直于 ∇In(i,j) 的方向。

实际操作

Inpainting方式

先计算 Ln(i,j)=Inxx(i,j)+Inyy(i,j)
再算

N→(i,j,n)|N→(i,j,n)|:=(−Iny(i,j),Inx(i,j))(Iny(i,j))2+(Inx(i,j))2−−−−−−−−−−−−−−−−−−√

再弄 δLn−→−(i,j)=(Ln(i+1,j)−Ln(i−1,j),Ln(i,j+1),Ln(i,j−1))
再算

δLn−→−(i,j)N→(i,j,n)|N→(i,j,n)|

理论上这样基本的东西就算完了，但是论文中说为了增加数值稳定性，多计算了一个系数

|∇In(i,j)|=⎧⎩⎨⎪⎪(Inxbm)2+(IxfM)2+(Inybm)2+(IyfM)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√,(InxbM)2+(Ixfm)2+(InybM)2+(Iyfm)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√,if βn>0if βn>0

具体含义就不说了。

扩散过程

为了保证方向场的正确的演变，在填充过程中，需要加入扩散过程。一般是执行几次填充，再执行几次扩散。采用各向异性的扩散，从而防止边界被抹平。
论文中说加入扩散过程是为了防止弯弯曲曲的线交错。

∂I∂t(x,y,t)=gϵ(x,y)κ(x,y,t)|∇I(x,y,t)|,∀(x,y)∈Ωϵ

其中， Ωϵ 是 Ω 的膨胀，半径是 ϵ 。 κ 是等照度线的曲率，最后 gϵ(x,y) 是在 Ωϵ 的光滑函数，其在 ∂Ωϵ 为0，在 Ω 内部为1.

实际操作

取 Ωϵ , 计算Inpainting，这也就可以将 Ωϵ−Ω 的信息propagate进 Ω 内部。当然我们不要改动 Ωϵ−Ω 的内容。
论文中采用每15次Inpainting操作，2次扩散操作， Δt=0.1

Simultaneous Structure and Texture Image Inpainting

这篇论文的主要思想是，将图像进行分解，分解成结构和纹理。其中结构部分用扩散方式的Inpainting，而纹理部分采用采样的方式生成。

图像分解

图像分解方法采用 Modeling textures with total variation minimization and oscillating patterns in image processing 方法。
认为图像 I=u+v ，其中 u 是structure，而 v 是纹理和噪声。

纹理生成

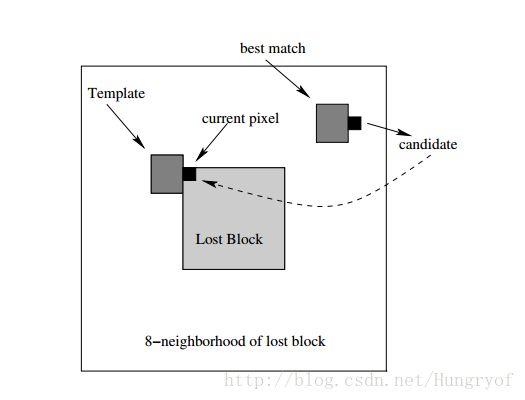
对于 v ，直接用下面的方式进行填充内部。从外面往里面填，先找最外圈的每个点，每个点会有一个与之相邻的图像小块（固定3*3,5*5之类的），图中显示的是”Template”，然后”Template”匹配 Ω¯¯¯ 的一些块，这些块称为best match. 查找方式就是如果两块的像素平方误差小于一个阈值 T 就行。那么此时cadidate像素是：这个像素与best match的块的相对位置，与current pixel与Template的相对位置一致。对了，如果best match的块有多个，随机选择一个即可。

图像填充

这个填充的方式与上篇文章的几乎是一样的。就是

∂I∂t=∇(ΔI)∇⊥I

这个没啥好说的了，其实就是拉普拉斯算子（图像的一个光滑函数）的梯度沿着等照度线方向的投影。跟上面是一样的。显然当达到稳态时， ∂I∂t=0 ，此时 ∇(ΔI)∇⊥I=0 。则 ΔI 为常数（沿着 ∇⊥I 方向）。
值得注意的是，进行这种基于diffusion的Inpainting，每进行几次Inpainting，就要进行一次各向异性的diffusion。

Object removal by examplar-based inpainting

以前都是慢慢往里面填充，比如diffusion的方式，或是前面一篇，都是一个点一个点往里面填，速度慢。这篇论文开始一块一块直接往里面填入。
直接看图：

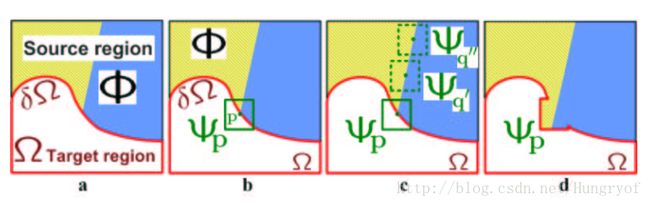
大体流程

我们要往里面填入，那么有没有填的快一点的，不要一个点一个点了，直接一块一块往里塞。那直接找边缘 δΩ 上的点呗，比如对于 p 点，我们以其为中心切块，得到 Ψp 。查找 Ω¯¯¯ 部分的小块，找到 Ψq′ 和 Ψq′′ 都与之很近，那么随便选一个吧，“替换掉” Ψp 即可。注意，只要从 Ψ′q 切出 Ψp 缺失的那部分，往里面填入即可，不要全部贴过来。
另外一点是，这个 p 点的填充顺序不是随便指定的，而是按照一定的优先级。我们首先可以从 δΩ 的每个点 p 得到很多的小块，这写小块会被赋予一个优先级，优先级从高到低，分别查找其与 Ω¯¯¯ 的小块中最近的，然后将最近的块的相应部分替换之。

具体方法

每个点： 具体值，以及 confidence value。这个confidence value一旦被填充了，则值固定不变。
同时对于 δΩ 区域的patch会有一个优先级(priority value)，这个优先级会决定它们的填充顺序。

P(p)=C(p)D(p)

前一项是confidence term，后面是data term。
那么

C(p)=∑q∈Ψp⋂Ω¯C(q)|Ψp|

所以就是 Ψp 中的 Ω¯¯¯ 区域的像素的confidence value的均值，作为 Ψp 的confidence.

D(p)=∇I⊥p⋅npα

其中 α=255 (对于灰度图像)。

也就是说，块的优先级一方面决定于其内部的点的优先级（含high confidence的像素越多，优先级越高 C(p) ）。
另一方面， D(p) 是论文的核心。这一项的构造可以促使线性结构优先生成。
而另一方面，该论文还考虑了，往内部填充我们还是要遵循不要破坏等照度线（主要体现在图像边缘上），即保持边缘不被破坏。那么自然就会想到 ∇I⊥p , 但是其实边缘的具体形状还是要考虑的，加入一个垂直于边缘 δΩ 的单位向量 np ， ∇I⊥p⋅np 会使得这个优先级即考虑等照度线优先保持，同时也会考虑边缘的具体形状。显然 D(p 会使得 具有线性结构的纹理优先生成。因为在线性结构处，那么等照度线一般会与 np 挨的比较近。如果在非线性结构处，那么等照度线几乎是于 δΩ 相切的，那么 np 又垂直于 δΩ ，所以优先级自然会很低。
最后附加文中说的一段话:
There is a delicate balance between the confidence and data terms. The data term tends to push isophotes rapidly inward, while the confidence term tends to suppress precisely this sort of incursion into the target region. As presented in the results section, this balance is handled gracefully via the mechanism of a single priority computation for all patches on the fill front.

填充伪代码：

忘说了，就是当用 Ψp^ “替换” Ψq^ 之后，那么 Ψq^ 的空白区域 ∀p|p∈Ψp^⋂Ω 的优先级 C(p) 怎么算，对，就直接用 Ψq^ 相应位置的点的优先级就行。或是说， Ψq^ 不仅是将值传入未知区域，也同时将优先级也传入到相应的未知区域。

Shift-Map Image Editing

总说

其实这个可以用来做多个东西，Inpainting只是其中一个方面。他的一个应用方面就是，retargeting，翻译是图像重定向。就是说有时候拍的图片长宽比例让你不爽，于是你直接rescale，你就会发现里面的人不是拉长了就是压短了。你会觉得很无奈。不过retargeting就是可以解决这个问题。
先给一张图：

其实核心方法就是，它会删除原图的某些不重要的像素。比如最后一幅图白色线抹去了，诡异的是，你发现路的开头还是有的，但是后面的线直接断了。其实人观察一幅图会更加关注前面的鸟，所以附带线就有了～～而如何知道人观察一幅图关注图的哪些部分呢？这是另一个分支，研究图的哪些部分人的关注程度，称之为saliency map.
不论是 retargeting, inpainting还是object rearrangement, 这些操作都可以用一个shift-map来表示：输出图的每个像素，其相对于输入图的像素的偏移。 比如，输出图的某个点 (x,y) ，这个点是由原图 (x+Δx,y+Δy) 的点过来的。因为输出图的点全部来自与输入图，所以没问题。

Graph labeling

把图看成一个graph labeling问题。graph labeling简单就是说，对于每个像素看个图的一个结点，给每个结点赋予一个label，从而使得某个能量函数最优。
输入图是 I(x,y) ， 输出图是 R(u,v) ，从而定义shift-map

M(u,v)=(tx,ty)

即输出图的 R(u,v) , 这个点对应的shift-map的值是 (tx,ty) , 那么 R(u,v) 其实是 I(u+tx,v+ty) 。
最优的shift-map定义成graph labeling问题，其中每个输出像素都被赋予一个label，即shift值 (tx,ty) ，损失函数：

E(M)=α∑p∈REd(M(p))+∑(p,q)∈NEs(M(p),M(q))

前面是数据项，后面是平滑项。论文中使用multi-label graph cuts来解决这个问题。

数据项

对于不同的任务，数据项的定义是不一样的。
比如 removal的话，我们可以让输入图的特定点在输出图消失。如果用saliency map的话， S(x,y) 大，则应该被移除。有：

Ed(M(u,v))=S(u+tx,v+ty)

点对的平滑项

Es(M(p),M(q)) 是用shift-map上的非连续性来表示我们加在输出图中的非连续性。
直接看公式：

Es(M)=∑(u,v)∈R∑i(R(u,v)+ei)−I((u,v)+M(u,v)+ei))2+β∑(u,v)∈R∑i(∇R(u,v)+ei)−∇I((u,v)+M(u,v)+ei))2

说明不仅考虑pixel value还考虑了相应的梯度。其中 ei 就是四个单位向量，代表像素点的四个邻域。所以简单的说就是，输出图的一个点 (u,v) ，它实际上来自输入图的 (u+tx,v+ty) 点，那么输出图的 (u,v) 点的邻域 R(u,v)+ei 与输入图的对应的那些邻域点 (u,v)+M(u,v)+ei 的像素差以及梯度差。

Graph labeling的层级解决方案

这个其实没啥好说的，就是现在的多分辨率方案。先在低分辨的图上进行graph labeling，得到相应的shift-map，然后上采样, 上采样后的图像的初始shift-map就用相应的shift-map进行最近邻插值就行（防止出现非整数）。那么现在不用全局优化函数了，只需要在插值后的shift-map的“邻域”找就行。论文中就是直接在每个点的八邻域中寻找。
论文中建立了五层，最开始是 100×100 ，然后。。。

如何进行Inpainting

其实只要将不想要的区域的saliency map的数据项标记成为无穷大就行。

PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing

PS从CS5开始有了填充功能，他们称之为Content-Aware-Fill，其实PS的填充就是PatchMatch与“Space-time video completion”的结合。PatchMatch是2009年出的，所以也就是为什么2010年CS5发行采用填充这个功能。

算法

这篇论文的主要工作就是快速查找最近邻图像块，称为NNF(nearest-neighbor field)。NNF是一个函数 f:A↦R2 , 代表偏移。就是图像 A 的以 a 为中心点的图像块, 该图像块与 B 图像中的以 b 为中心点的图像块距离最近。那么 f(a) 就是 b−a ，即坐标点相减就行。（这个和shift-map有较大区别，shift-map是以 B 图为主体，强调 B 图中的每个点，原本来源于 A 图的哪个点。而patchMatch是以 A 图为主体，强调 A 图的块，可以从 B 图找到最近的一块。）
算法主要分为两个个步骤：
1. 初始化（随机即可）
2. 迭代：Propagation以及Random Search，交替进行。

初始化

初始化没啥好说的，用均匀分布初始化就行。一般来说，算法是先初始化，再迭代。再上采样，再迭代….都是遵循coarse-to-fine的方式。那么上采样时，初始化更高分辨率的NNF时，这里有点特殊。论文中是将两种进行结合：
1. 直接上采样（nearesetUpSample）初始化
2. 随机初始化
然后再将两个初始化结合，对每个点，从两种NNF中选择最好的（直接比两个图像对的距离，选择距离小的那个NNF）从而形成这个分辨率的NNF初始化。

Propagation

核心思想是这样的，如何改进 f(x,y) 呢？根据图像的局部相似性，我们知道图像的局部的点是相似的，那么显然 f(x,y) 附近的点的NNF f(x−1,y) 之类的，它们很可能是映射到 B 同一个块上。假设 f(x−1,y) 是一个好的匹配（good match，两块已经达到距离最近), 那么我们可以把这个好的匹配传播到 f(x,y) 上。这就是“Propagation”的由来。 f(x−1,y) 如果是好匹配，那么其所对应的 B 图像块的右边的那一块，没准就是 A 图的 (x,y) 块的一个更好的匹配。
既然是这样，那么对于 f(x,y) ，我们检查其周围的点（正左方，正上方）的匹配 f(x−1,y) , f(x,y−1) ，看看这些匹配在 B 中的块，这些块的正右方、正下方的那些块就是我们要比较的。

公式化点的方式就是，我们想改善最近邻偏移 f(x) ,那么我们将 f(x) 与 f(x−Δp)+Δp 进行比较，从而其中 Δp 取(1,0)或是(0,1)。

举个具体例子解释：

假设有 (10,20)→(40,80) ，即图 A 的 (10,20) 块（实际上是以(10,20)为中心的块，简便说明），那么它对应的 B 中的块 (40,80) ，那么记录成 f(10,20)=(30,60) 。我们要改进 f(10,20) ，那么看 f(9,20) 和 f(10,19) 。假设 f(9,20)=(21,44) ， f(10,19)=(16,52) 。那么我们找到“这些块”为 B 中的 (30,64) 以及 (26,71) 。然后看“这些块”的正右方、正下方，分别为 (31,64) 以及 (26,72) 。所以最终是看 A 中的块 (10,20) 与 B 中的三个块 (40,80) , (31,64) , (26,72) 的哪一块最近。从而改善 f(10,20) .

显然如果 (x,y) 是一个good match，并且这个点所在的局部相似区域为 R ，那么 R 区域中， (x,y) 的右边和下方都会是good match。
最后一点是，奇数次迭代时，Propagation顺序是从左到右，从上到下；偶数次反过来的顺序。

Random Search

虽然Propagation收敛特别快，但是特别容易陷入局部最小。Random Search通过将每个点检查其周围的点的匹配，从而更新该点的匹配，从而消除这个问题。
对于某个点(x,y)，其在 B 中的匹配是 v0 点，那么我们需要检查一下 v0 点的周围是不是存在着与(x,y)点的更好的匹配呢？

ui=v0+wαiRi

其中 ui 就是候选点， Ri 是 [−1,1]×[−1,1] ， w 是搜索范围， α 是一个固定的比例。让 i=0,1,2,... ，当然了 wαi 不要小于1就行。

Editing Tools

这个挺有意思的，就是可以交互性的填充。 简单来说就是自己限定缺失区域的点的label与外部区域的点的label。第二幅图，用红色来将右边的白色花移动到左边。

The Generalized PatchMatch Correspondence Algorithm

总说

这篇是PatchMatch的改进，改进主要有以下三点：
1. 查找k个最近邻（以前是查找与一个，即每个点只有一个NNF）
2. 跨尺度以及旋转角度的搜索
3. 可以用任意的算子和距离计算，而不仅仅是平方误差和。
第一点就是，比如对于object detection，我们希望对于每个查询的patch，能找到多个匹配。
第二点就是，对于超分辨，输入可以是不同的尺度的，而object detection也是希望不同旋转角度的物体都能检测。
第三点就是，对于物体识别，图像块对于外观和几何形状改变来说，不够鲁棒。

k neaerest neighbors

这个没啥好说的，就是以前NNF只有一个值，现在对于每个点有多个就行。propagation和random search检查的点，都相当与乘以k。

Enrichment

原先的propagation只是将good matches沿着矩形网格进行传播，而这里是将good matches沿着graph进行传播。图中的每个点就是它的KNN。

前向 enrichment

f→: 具有k个值的NNF
f2−→ : k个最近邻的最近邻，共有 k2 个，可能有些值出现多次。
那么这个升级版的NNF就是：
f′→=min(f→,f2−→)

反向 enrichment

f−1: 对B图中的每个点都有 k 个最近邻。若 f−1(a) 表示这些点，这些点的 k 个最近邻中有点 a 。
显然 f−1(a) 可能为0，（B中的点没有与a是“k最近的”）
f−1(a) 可能有多个
f′′=min(f,f−1)

Rotations and scale

定义NNF：
f:R2↦R4
就是对于 A 图的一个点，则不再映射到另一个点，而是一个四元组 (x,y,θ,s) 。 f 初始化直接用随机位置，角度以及尺度。在propagation阶段，邻接的patch不再是由简单的位移来表示，而是要用雅克比矩阵来表示相对的偏移。
假设矩阵记为 T(f(x)) ，那么 f(x−Δp)+T(f(x−Δp))Δp 就是候选点。
同理，在Random Search阶段，直接所有参数都是按照指数递减的就行。

Image Completion Approaches Using the Statistics of Similar Patches

总说

这篇的Introduction写的挺全面的。
这篇论文的核心思想就是，一幅图像内部，相似的图像块之间的offset的统计结果是稀疏的。

比如这幅图，最相近小块之间的offset基本就是几个特定的值。
以前的填充，直接是从外部找最近的小块，一般不考虑这些offset的值是否太大还是太小。这篇论文在匹配时引进了offset的统计信息（用直方图），只在特定的几个offset中找到最匹配的块！不再是全局查找了。

统计patch offset的信息

s(x)=argmins∥P(x+s)−P(x)∥2s.t.|s|>τ

这个 τ 是一个阈值，从而去除空间过近的相似块。
然后计算直方图

h(u,v)=∑xδ(s(x)=(u,v))

等式成立， δ(⋅) 为1，否则为0.
论文中，取了K=60个主要的offsets。

利用主要的offsets进行填充

因为基于样本的又可以分为基于graph labeling以及matching patches的。比如Shift-map就是前者，PatchMatch就是后者。前者就是定义一个能量函数，数据项和平滑项，然后用graph cut通用算法来解。后者采用直接找最近块匹配。这篇论文的相似块偏移量的统计信息可以用于两种方法。

Graph-based

给定 k 个主要的offsets，将这 k 个偏移进行融合。

E(L)=∑x∈ΩEd(L(x))+∑(x,x′)∣x∈Ω,x′∈ΩEs(L(x),L(x′))

L 是Labeling map, 注意： L 将一个label给 x ，而这个label只能从 {si}ki=1 或是 s0=(0,0) 中选取。即每个点要么不变，要么只能用主要的offsets中的一个，其中 s0=(0,0) 只对图像边界点才可选，否则没啥意思。

Ed={0,∞,if x+s∈Ω¯¯¯otherwise

这样设计数据项，可以保证填入的都是用 Ω¯¯¯ 的点。
平滑项的定义：

Es(a,b)=∥I(x+sa)−I(x+sb)∥2+∥I(x′+sa)−I(x′+sb)∥2

值得注意的是: x,x′ 是 Ω 中的相邻点，是four-connected的。

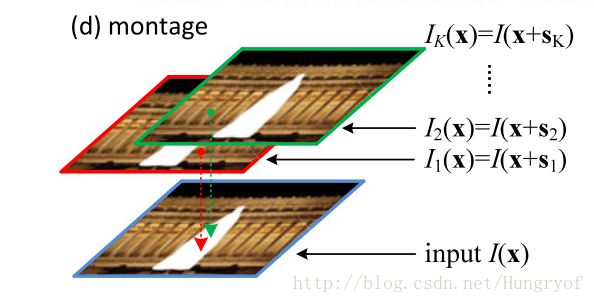
看图，如果 x,x′ 分别用了两个不同的offset map, 那么 x 和 x′ 之间很可能会出现裂缝。所以这样定义的平滑项可以减少裂缝的出现。

Matching-based

这个真的没啥好说的，

∑x∈Ωmin1≤i≤K∥P(x)−P(x+si)∥2

其中只能是从 {si}ki=1 里面取offset