强化学习笔记01:马尔科夫决策过程与动态规划
Markov Decision Process and Dynamic Programming
- Date: Match 2019
- Material from Reinforcement Learning:An Introduction,2nd,Rechard.S.Sutton;
- Code from dennyBritze, 部分做了修改;
文章目录
- Markov Decision Process and Dynamic Programming
- MDP problems set up
- Bellman Equation
- Optimal Policies and Optimal Value Functions
- Dynamic Programming
- Policy Evaluation
- Example: Gridword
- Policy Improvement
- policy improvement theorem
- Policy Iteration
- Value Iteration
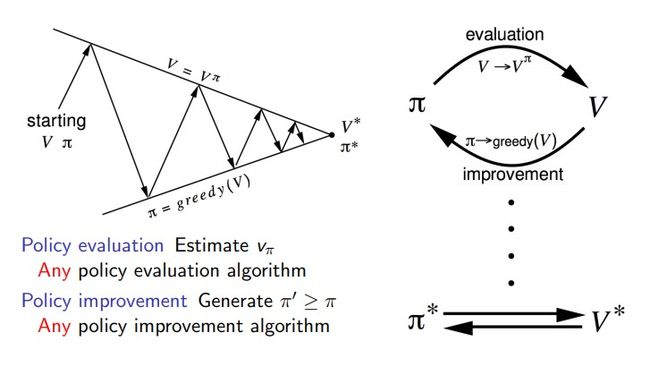
- Generalized Policy Iteration(GPI)
Abstract
MDP过程是RL环境中常见的范式,DP是解决有限MDP问题的可最优收敛办法,效率在有效平方级。DP算法基本思想是基于贝尔曼方程进行Bootstrapping,即用估计来学习估计(learn a guess from a guess)。DP需要经过反复的策略评估和策略提升过程,最终收敛到最优的策略和值函数。这一过程其实是RL很多算法的基本过程,即先进行评估策略(Prediction)再优化策略。
MDP problems set up
在RL problems set up中我们知道RL基本要素是Agent和Enviornment, 环境的种类很多,但大多都可以抽象成一个马尔科夫决策过程(MDP)或者部分马尔科夫决策过程(POMDP);
MDPs are a mathematically idealized form of the reinforcement learning problem for which precise
theoretical statements can be made.
Key elements of MDP: < S , A , P , R , γ > <\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R},\gamma> <S,A,P,R,γ>
| 名称 | 表达式 |
|---|---|
| 状态转移矩阵(一个Markov Matrix) | $P_{ss’}^a=P(S_{t+1}=s’ |
| 奖励函数 | $R_{s}^a=\mathbb{E}{\pi}[R{t+1} |
| 累计奖励 | G t = ∑ k = 0 ∞ γ k R t + 1 + k G_t=\sum_{k=0}^\infty\gamma^k R_{t+1+k} Gt=∑k=0∞γkRt+1+k |
| 值函数(Value Function) | $V_\pi(a)=\mathbb{E}[G_t |
| 动作值函数(Action Value Fucntion) | $Q_\pi(s,a)=\mathbb{E}[G_t |
| 策略(Policy) | $\pi(a |
| 奖励转移方程 | R t + 1 = R t + 1 ( S t , A t , S t + 1 ) R_{t+1}=R_{t+1}(S_t,A_t,S_{t+1}) Rt+1=Rt+1(St,At,St+1) |
| 某策略下的状态转移方程 | $P_{ss’}^\pi=\mathbb{P}(S_{t+1}=s’ |
| 某状态某策略下的奖励函数 | $R_{s}^\pi=\sum_{a}\pi(a |
Bellman Equation
贝尔曼方程将某时刻的值函数与其下一时刻的值函数联系起来:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... Gt=Rt+1+γRt+2+γ2Rt+3+...
G t = ∑ k = t + 1 T γ k − t − 1 R k = R t + 1 + γ G t + 1 G_t = \sum_{k=t+1}^{T}\gamma^{k-t-1}R_k = R_{t+1} + \gamma G_{t+1} Gt=k=t+1∑Tγk−t−1Rk=Rt+1+γGt+1
对于动作-值函数来说:
KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲\nonumber Q…
对于值函数来说
KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲\nonumber V…
基于公式2可以写成矩阵的形式: V π = R s π + P π V π V^\pi = R_s^\pi + P^\pi V^\pi Vπ=Rsπ+PπVπ
Optimal Policies and Optimal Value Functions
最优策略和最优的值函数关系如下:
v ∗ = max π V π ( s ) v_* = \max_\pi V_\pi(s) v∗=πmaxVπ(s)
Q ∗ ( s , a ) = max π Q p i ( s , a ) Q_*(s,a) = \max_\pi Q_pi(s,a) Q∗(s,a)=πmaxQpi(s,a)
V ∗ ( s ) = max a Q ∗ ( s , a ) V_*(s) = \max_a Q_*(s,a) V∗(s)=amaxQ∗(s,a)
Find optimal policy by:
KaTeX parse error: No such environment: equation at position 12: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \pi_{*…
在最优策略下的贝尔曼方程为Bellman Optimality Equation:
KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ Q_*(s,a)&=…
KaTeX parse error: No such environment: eqnarray at position 17: … \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲\label{BOEQ2} …
Dynamic Programming
DP算法要求MDP的全部信息完全可知,依据Bellman Optimality Equation为基本思想进行策略迭代出最优结果;
Policy Evaluation
策略评估是在给定一个策略的情况下计算出Value Function的过程,迭代的更新规则是:
v k + 1 ( s ) = E π [ R t + 1 + γ v k ( S t + 1 ) ∣ S t = s ] v_{k+1}(s) = \mathbb{E}_\pi[R_{t+1} + \gamma v_k(S_{t+1})|S_t = s] vk+1(s)=Eπ[Rt+1+γvk(St+1)∣St=s]
= ∑ a π ( a ∣ s ) ∑ s ′ P s s ′ a ( R s s ′ + γ v k ( s ′ ) ) =\sum_a \pi(a|s)\sum_{s'}P_{ss'}^{a}(R_{ss'}+\gamma v_k(s')) =a∑π(a∣s)s′∑Pss′a(Rss′+γvk(s′))
迭代一定次数后 v π v_\pi vπ会趋于稳定,评估结束。
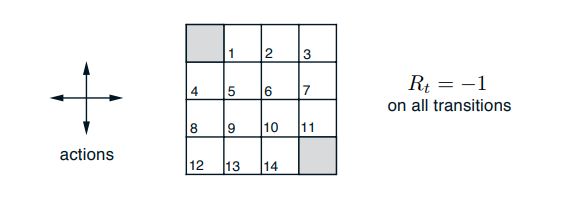
Example: Gridword
探索出发点到终点的路径,动作空间是四个方向, 除了终点其他坐标的Reward均为-1
import gym
import gym_gridworlds
import numpy as np
# 策略评估算法
def policy_val(policy, env, GAMMA=1.0, theta=0.0001):
V = np.zeros(env.observation_space.n)
while True:
delta = 0
for s in range(env.observation_space.n):
v = 0
for a, action_prob in enumerate(policy[s]):
for next_state, next_prob in enumerate(env.P[a,s]):
reward = env.R[a, next_state]
v += action_prob*next_prob*(reward + GAMMA*V[next_state])
delta = max(delta, V[s]-v)
V[s] = v
if delta < theta:
break
return np.array(V)
env = gym.make('Gridworld-v0')
# 初始随机策略
random_policy = np.ones((env.observation_space.n, env.action_space.n)) / env.action_space.n
# 评估这个随机策略得到稳定的Value Function:
policy_val(random_policy, env)
array([ 0. , -12.99934883, -18.99906386, -20.9989696 ,
-12.99934883, -16.99920093, -18.99913239, -18.99914232,
-18.99906386, -18.99913239, -16.9992679 , -12.9994534 ,
-20.9989696 , -18.99914232, -12.9994534 ])
Policy Improvement
定义:The process of making a new policy that improves on an original policy, by making it greedy with
respect to the value function of the original policy, is called policy improvement.
policy improvement theorem
假设 π \pi π和 π ′ \pi' π′是两个确定的策略,对于所有的 s ∈ S s\in \mathcal{S} s∈S
如果 q π ( s , π ′ ( s ) ) ≥ v π ( s ) q_\pi(s, \pi'(s)) \ge v_\pi(s) qπ(s,π′(s))≥vπ(s)
那么可以证明得到:
v π ′ ( s ) ≥ v π ( s ) v_\pi'(s) \ge v_\pi(s) vπ′(s)≥vπ(s)
所以策略提升的过程就是:KaTeX parse error: Expected 'EOF', got '\mbox' at position 22: …xleftarrow[]{} \̲m̲b̲o̲x̲{Greedy}(V_\pi)…
Policy Iteration
Policy Iteration = Policy Evaluation + Policy Improvement
给定策略–评估策略得到各个V(s)–greedy提升出新的策略–评估新策略–直到策略不发生变化
def one_step_lookahead(state, V, GAMMA):
A = np.zeros(env.action_space.n)
for a in range(env.action_space.n):
for next_state, prob in enumerate(env.P[a, state]):
reward = env.R[a, next_state]
A[a] += prob * (reward + GAMMA*V[next_state])
return A
def policy_improvement(env, policy_eval_fun=policy_val, GAMMA=1.0):
# 用随机策略开始
policy = np.ones((env.observation_space.n, env.action_space.n)) / env.action_space.n
while True:
V = policy_eval_fun(policy, env, GAMMA)
policy_stable = True
for s in range(env.observation_space.n):
chosen_a = np.argmax(policy[s])
action_values = one_step_lookahead(s, V, GAMMA)
best_a = np.argmax(action_values)
# 贪心的方式更新策略
if chosen_a != best_a:
policy_stable = False
policy[s] = np.eye(env.action_space.n)[best_a]
if policy_stable:
return policy, V
# 得到稳定的策略和V(s)
policy_improvement(env)
(array([[1., 0., 0., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 1., 0., 0.]]),
array([ 0., 0., -1., -2., 0., -1., -2., -1., -1., -2., -1., 0., -2.,
-1., 0.]))
Value Iteration
跟Policy Iteration的区别在于省略Policy Evaluation的过程为一步计算,这样降低了迭代次数,同时保证收敛结果依然为 v ∗ v_* v∗,边评估边提升。
省略后的Evaluation:
v k + 1 ( s ) = max a ∑ s ′ P s s ′ a ( R s ′ a + γ v k ( s ′ ) ) v_{k+1}(s) = \max_a \sum_s' P_{ss'}^a(R_{s'}^a + \gamma v_k(s')) vk+1(s)=amaxs∑′Pss′a(Rs′a+γvk(s′))
而之前的评估策略迭代更多:
v k + 1 ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ P s s ′ a ( R s s ′ + γ v k ( s ′ ) ) v_{k+1}(s) = \sum_a \pi(a|s)\sum_{s'}P_{ss'}^{a}(R_{ss'}+\gamma v_k(s')) vk+1(s)=a∑π(a∣s)s′∑Pss′a(Rss′+γvk(s′))
def value_iteration(env, theta=0.001, GAMMA=1.0):
V = np.zeros(env.observation_space.n)
while True:
delta = 0
for s in range(env.observation_space.n):
A = one_step_lookahead(s, V, GAMMA)
best_action_value = np.max(A)
delta = max(delta, np.abs(best_action_value - V[s]))
V[s] = best_action_value
if delta < theta:
break
policy = np.zeros((env.observation_space.n, env.action_space.n))
for s in range(env.observation_space.n):
A = one_step_lookahead(s, V, GAMMA)
best_action = np.argmax(A)
policy[s, best_action] = 1.0
return policy, V
value_iteration(env)
(array([[1., 0., 0., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 1., 0., 0.]]),
array([ 0., 0., -1., -2., 0., -1., -2., -1., -1., -2., -1., 0., -2.,
-1., 0.]))
可以看出同一个环境,Value Iteration的结果和之前Policy Iteration的结果相同;
Generalized Policy Iteration(GPI)
GPI的思想将会贯彻RL始终,任何RL算法的过程都可以看作是一个GPI的过程。GPI描述了policy evaluation和improvement不断交互提升的过程;评估和提升的方法是多样的。