机器学习笔记（一）微积分

微积分

@(Machine Learning)[微积分, 概率论]

1.夹逼定理：

当 x∈U(x0,r) 时，有 g(x)≤f(x)≤h(x) 成立，并且 limx→x0g(x)=A,limx→x0h(x)=A 那么：

limx→x0f(x)=A

2.极限存在定理：

• 单调有界数列必有极限
  
  • 单增数列有上界，则其必有极限

3.导数：

导数就是曲线的斜率，是曲线变化快慢的反应。
- 二阶导是斜率变化快慢的反应，表征曲线的凹凸性，但是方向呢总是指向轨迹曲线凹的一侧。

常用函数的导数：
C′=0
(xn)′=nxn−1
(sinx)′=cosx
(cosx)′=−sinx
(ax)′=axlna
(ex)′=ex
(logax)′=1xlogae
(lnx)′=1x

(u+v)′=u′+v′
(uv)′=u′v+uv′

重要应用：幂指函数（牢记套路）

• 已知函数 f(x)=xx,x>0 ， 求 f(x) 的最小值：
• 解：
  
  • t=xx
  • 取指数———> lnt=xlnx
  • 两边对x求导———> 1tt′=lnx+1
  • 令 t′ 等于0（取驻点求最小值）———> lnx+1=0
  • x=e−1
  • t=e−1e
    

    上面就是求 幂指函数的一般套路，像求 最大似然估计一定会用到这个套路
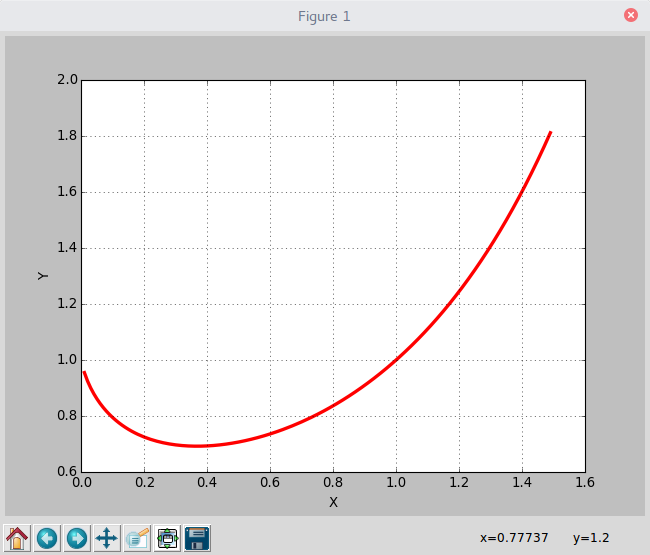
    看一下结果和代码:
    

# -*- coding:utf8 -*-
import math
import matplotlib.pyplot as plt

if __name__ == '__main__':
    x = [float(i)/100 for i in range(1,150)]
    y = [math.pow(i,i) for i in x]
    plt.plot(x, y, 'r-', linewidth = 3, label = 'y(x)=x^x')
    plt.grid(True)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()

---

4.Taylor公式 — Maclaurin公式

如果我们知道了函数的一阶导，二阶导。。n阶导就可以写出 x0 泰勒公式：一阶导×差距+二阶导×差距除以阶乘到最后x的一个高阶无穷小（扔掉）。

f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+....+fn(x0)n!(x−x0)n+Rn(x)

如果我们把 x0 换成0便得到了迈克劳林公式。

f(x)=f(0)+f′(0)x+f′′(0)2!x2+....+fn(0)n!xn+o(xn)

Taylor公式的应用:

• 数值计算：初等函数值的计算（在原点展开）
  
  • sinx=x−x33!+x55!−x77!+x99!+......+(−1)m−1x2m−1(2m−1)!+R2m
  • ex=1+x+x22!+x33!+.....+xnn!+Rn

当一个公式不好求的时候，我们可以把他泰勒展开，并且可以把泰勒公式看成一个多项式加权的和。
当然实践中我们往往需要做一定程度的变换：
比如给定一个正实数x，计算 ex=?
- 当 x=0.01 的时候，带入泰勒求解就可以，但是如果 x=100 的话，那这个计算量和误差就会发散，
- 所以我们用另一种思路：
- 求整数k和小数r，使得
- x=k∗ln2+r,|r|<=0.5∗ln2
- 从而：
- ex=ek∗ln2+r
=ek∗ln2∗er
=2k∗er (这里 r 是小于1的，所以 er 必收敛，而且2的k次方也容易计算)

5.方向导数：

如果函数 z=f(x,y) 在点 P(x,y) 是可微分的，那么，函数在该点沿任意方向 L 的方向导数都存在，且有：

∂f∂l=∂f∂xcosϕ+∂f∂ysinϕ

- 等式的右侧第一项的系数 ∂f∂x 其实就是假定y是常数求x的导数， ∂f∂y 同理
- 其中， ϕ 为 x 轴到方向 L 的转角。

6.梯度：

那么梯度是什么呢？梯度就是把上面方向导数的系数提出来组成的向量。
- 设函数 z=f(x,y) 在平面区域D内具有一阶连续偏导数，则对于每一个点 P(x,y)∈D ,向量

(∂f∂x,∂f∂y)

为函数在点P的梯度，记做 gradf(x,y) ， 总之就是各对xy求偏导形成的向量
- 梯度的方向是函数在该点变化最快的方向
退化一点想，如果只含有一个变量x，即 z=x2 ，那么我们的轨迹就退化成一个简单的二次函数，梯度也就变成了 ∂f∂x 或者说是 dfdx 。
所以说梯度就是一元的导数在高元的推广而已，一个数换成了一个向量。

---

7.凸函数：

7.1凸函数的定义：

若函数f的定义域domf为凸集，且满足 ∀x,y∈domf,0≤θ≤1 ,有

f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)

换句话说凸函数两个点之间的连线一定在曲线之上。
- 假设 θ=0.9 ，不等式左边就是曲线上的点，右边就是割线上的点。我们在图上直观画出来就是：
简单来说就是： 割线在上，函数在下。

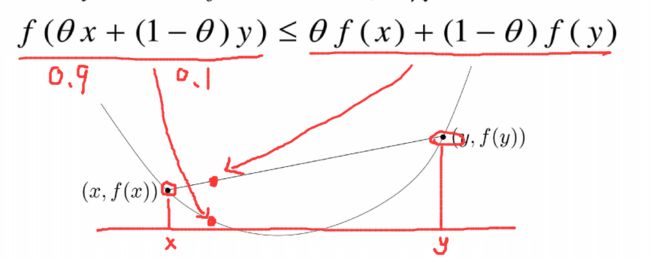
在机器学习领域，我们就把他叫做凸函数，不是什么数学上翻译的下凹，凹函数 。。。。

7.2凸函数的判定：

定理： f(x) 在区间 [a,b] 上连续在 (a,b) 内二阶可导，那么：
- 若 f′′(x)>0 ，则 f(x) 是凸的
- 若 f′′(x)<0 ，则 f(x) 是凹的
即：一元二阶可微的函数在区间上是凸的，当且仅当它的二阶导数是非负的。

7.3凸函数定义的扩展：

定义里我们的 θ 是0.9，另一项是0.1。其实这些系数就是两个项的权重，现在我们变成n个项，分散一下权重，就有了另一公式：

f(θ1x1+....+θnxn)≤θ1f(x1)+....+θnf(xn)

, 其中 0≤θi≤1,θ1+θ2+....+θn=1
- 当我们知道了函数是凸函数时，我们往往会利用这个不等式进行一些证明。

7.4凸性质的应用（很简单大家耐心看）：

我们用这个性质来证明一下:在x中取值的两个概率分布 p(x),q(x) 为什么相对熵(KL散度)是 ≥0 的：

D(p||q)=∑xp(x)logp(x)q(x)=Ep(x)logp(x)q(x)≥0

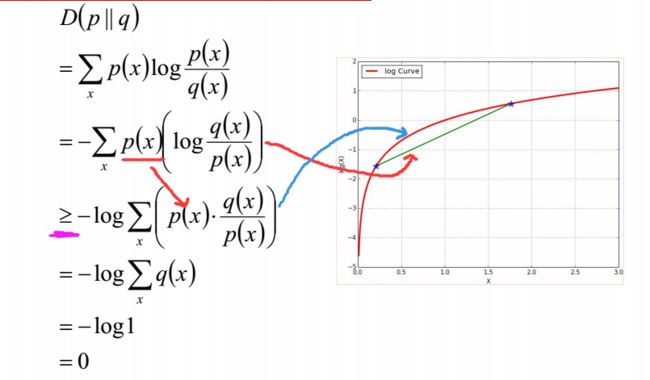
• 在推到过程中我们把 p(x)q(x) 看成一个数，那么第二步中， p(x)logp(x)q(x) 就相当于一个权值乘以一个数，回顾上面的凸函数公式，不难看出它就是绿色的线上的某个点。
• 在第三步里，我们把 p(x) 移到 log 里面，所以可以看成它代表红色的线上的某个点。
• 但是别忘了前面的负号，所以是绿色的值大于等于红色。注意上图是 log 曲线。 −log 大家自行脑补了。
• q 的加和是1，所以最后为0
  并不难是吧～

---

参考文献：
邹博：七月算法-机器学习
Christopher M. Bishop, Pattern Recognition and Machine Learning,
Springer-Verlag, 2006
Kevin P. Murphy, Machine Learning:A Probabilistic Perspective,
The MIT Press, 2012
李航,统计学习方法,清华大学出版社,2012
Stephen Boyd,Lieven Vandenberghe, Convex Optimization,
Cambridge University Press, 2004
Thomas M. Cover, Joy A. Thomas, Elements of Information
Theory,2006
各章节特定的经典论文,如:
Alex Rodriguez, Alessandro Laio, Clustering by fast search and find of
density peak, Science 344.6191(2014)
David M. Blei, Andrew Y. Ng, Michael I. Jordan, Latent Dirichlet
Allocation, 2003