Kaggle项目之PUBG Finish Placement Prediction（一）——探索性分析

数据来自Kaggle，也可以在这里取，提取码wymx。比赛在一个月前结束，这里拿来练练手~
附加python代码！多图预警！！

0、问题背景

在PUBG游戏中，每场比赛最多有100名玩家（matchId）。 玩家可以在团队中（groupId）根据有多少其他团队在被淘汰时还活着而在游戏结束时排名（winPlacePerc）。 在游戏中，玩家可以拿起不同的弹药，恢复被击倒但未被击倒的队友，驾驶车辆，游泳，跑步，射击，并体验所有后果 - 例如跌得太远或者自己跑过来 消除自己。
您将获得大量匿名的PUBG游戏统计数据，其格式设置为每行包含一个玩家的游戏后统计数据。 数据来自所有类型的比赛：独奏，二重奏，小队和自定义; 不保证每场比赛有100名球员，每组最多4名球员。
你必须创建一个模型，根据他们的最终统计数据预测球员的完成位置，从1（第一名）到0（最后一名）。

1、各变量含义

DBNOs - 击倒多少敌人 
assists - 伤害过多少敌人（最终该敌人被队友杀害）
boosts - 使用过多少个提升性的物品(boost items used)
damageDealt - 造成的总伤害-自己所受的伤害
headshotKills - 通过爆头而杀死的敌人数量
heals - 使用了多少救援类物品
Id - 玩家ID
killPlace - 杀死敌人数量的排名
killPoints - 基于杀戮的玩家外部排名。将其视为Elo排名，只有杀死才有意义。如果rankPoints中的值不是-1，那么killPoints中的任何0都应被视为“无”。
killStreaks - 短时间内杀死敌人的最大数量
kills - 杀死的敌人的数量
longestKill - 玩家和玩家在死亡时被杀的最长距离。 这可能会产生误导，因为击倒一名球员并开走可能会导致最长的杀戮统计数据。
matchDuration - 匹配用了多少秒
matchId - 匹配的ID（每一局一个ID）
matchType -  单排/双排/四排；标准模式是“solo”，“duo”，“squad”，“solo-fpp”，“duo-fpp”和“squad-fpp”; 其他模式来自事件或自定义匹配。
rankPoints - 类似Elo的玩家排名。 此排名不一致，并且在API的下一个版本中已弃用，因此请谨慎使用。值-1表示“无”。
revives - 玩家救援队友的次数
rideDistance - 玩家使用交通工具行驶了多少米
roadKills - 在交通工具上杀死了多少玩家
swimDistance - 游泳了多少米
teamKills - 该玩家杀死队友的次数
vehicleDestroys - 毁坏了多少交通工具
walkDistance - 步行运动了多少米
weaponsAcquired - 捡了多少把枪
winPoints - 基于赢的玩家外部排名。将其视为Elo排名，只有获胜才有意义。如果rankPoints中的值不是-1，那么winPoints中的任何0都应被视为“无”。
groupId - 队伍的ID。 如果同一组玩家在不同的比赛中比赛，他们每次都会有不同的groupId。
numGroups - 在该局比赛中有玩家数据的队伍数量
maxPlace - 在该局中已有数据的最差的队伍名词（可能与该局队伍数不匹配，因为数据收集有跳跃）
winPlacePerc - 预测目标，是以百分数计算的，介于0-1之间，1对应第一名，0对应最后一名。 它是根据maxPlace计算的，而不是numGroups，因此匹配中可能缺少某些队伍。

import pandas as pd
origin_data = pd.read_csv('train_V2.csv')
print origin_data.shape
#origin_data.head()

(4446966, 29)

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns#数据可视化
import numpy as np

查看这些数据包含有47965局（47965次匹配）

print len(origin_data.groupby(['matchId']))

47965

2、探索性分析——单个变量

（1）整形(int)变量的分布

def feature_barplot(feature, df_train = origin_data, figsize=(15,6), rot = 90, saveimg = False): 
    feat_train = df_train[feature].value_counts()
    fig_feature, axis1, = plt.subplots(1,1,sharex=True, sharey = True, figsize = figsize)
    sns.barplot(feat_train.index.values, feat_train.values, ax = axis1)
    axis1.set_xticklabels(axis1.xaxis.get_majorticklabels(), rotation = rot)
    axis1.set_title(feature + ' of training dataset')
    axis1.set_ylabel('Counts')
    plt.tight_layout()
    if saveimg == True:
        figname = feature + ".png"
        fig_feature.savefig(figname, dpi = 75)

feature_barplot('DBNOs') #击倒敌人的分布

如果直接这样作图，会发现该图像呈现极为右偏的分布，其实，DBNOs超过6，7和8的人数就已经非常少了，因此将DBNOs>x的全部归为一类，那么x具体是多少更有说服力呢，一个精确的做法是：先找出99%的分位数，将大于99%分位数的归为一类。

origin_data['DBNOs_new'] = origin_data['DBNOs']
origin_data.loc[origin_data['DBNOs_new'] > origin_data['DBNOs_new'].quantile(0.99)] = 'larger'
plt.figure(figsize = (10,6))
sns.countplot(origin_data['DBNOs_new'].astype('str').sort_values())
plt.title('DBNOs')
plt.show

可见大部分玩家击倒敌人的数量为0

（2）连续变量的分布

造成的伤害值是一个连续变量（总伤害-自身受到的伤害）

#造成的伤害值的分布（总伤害-自身受到的伤害）
plt.figure(figsize=(10,6))
plt.title("Damage Dealt")
sns.distplot(origin_data['damageDealt']) #distplot直方图
plt.show()

对于那些击杀数为0的玩家，他们造成的伤害如何？

data_kill_0 = origin_data[origin_data['kills']==0]
plt.figure(figsize=(10,6))
plt.title("Damage Dealt by 0 killers",fontsize=15)
sns.distplot(data_kill_0['damageDealt'])
plt.show()
#del data_kill_0

步行距离也是一类连续变量，先找到均值和百分之99的分位数

print('The average person walks for {:.1f}m, 99% of {}m or less, while the marathoner champion walked for {}m.'
      .format(origin_data['walkDistance'].mean(), 
              origin_data['walkDistance'].quantile(0.99), 
              origin_data['walkDistance'].max()
             )
     )

The average person walks for 1154.2m, 99% of 4396.0m or less, 
while the marathoner champion walked for 25780.0m.

99%的人的步行距离都在4396m以下，而最大步行距离为25780m，为了图像不过分右偏，不考虑那1%的runners了

new_data = origin_data[origin_data['walkDistance'] < origin_data['walkDistance'].quantile(0.99)]
plt.figure(figsize=(10,6))
plt.title("The Running Distances")
sns.distplot(new_data['walkDistance']) #distplot直方图
plt.show()
del new_data

再看一下预测变量winPlacePerc的分布情况，winPlacePerc变量的取值在0-1之间

#得分winPlacePerc分布
def winplace_rank(x):
    if x < 0.1:
        return 'rank10'
    elif x < 0.2:
        return 'rank9'
    elif x < 0.3:
        return 'rank8'
    elif x < 0.4:
        return 'rank7'
    elif x < 0.5:
        return 'rank6'
    elif x < 0.6:
        return 'rank5'
    elif x < 0.7:
        return 'rank4'
    elif x < 0.8:
        return 'rank3'
    elif x < 0.9:
        return 'rank2'
    else:
        return 'rank1'

origin_data['winplace_rank'] = origin_data['winPlacePerc'].apply(winplace_rank)
feature_barplot('winplace_rank') #可见因变量的分布基本上是平衡的

可见最终的排名基本上是均衡的，不存在明显的不平衡。

2、探索性分析——两个变量

sns.jointplot(x = 'winPlacePerc', y = 'kills', data = origin_data, size=8, ratio = 3)
#ratio：Ratio of joint axes size to marginal axes height.
#kind : { “scatter” | “reg” | “resid” | “kde” | “hex” }, optional 
plt.show()

如果上图看不明显，可以用箱线图来看击杀敌人的数量和最终排名之间的关系

注意：
kills变量的分布是极度不平衡的，而winPlacePer的分布又基本上是平衡的
因此画两变量的箱线图时，应该把kills作为横坐标（自变量），而把winPlacePer作为纵轴（因变量）
如果反过来就基本上看不出来二者的关系了（因为kills为0的人相对特别多，它会把整个水平带偏，且极大值/异常值很多）如下图所示

正确的做法

#用pd.cut做变量切分/变量分箱
origin_data['kills_rank'] = pd.cut(origin_data['kills'], [-1, 0, 2, 5, 10, 20, 60] ,labels = ['0_kills', '1-2_kills', '3-5_kills', '6-10_kills', '11-20_kills', '20+kills'])
plt.figure(figsize = (10, 6))
sns.boxplot(x = 'kills_rank', y = 'winPlacePerc', data = origin_data)
plt.show()

对于步行的距离和最终排名之间的关系

sns.jointplot(x = 'winPlacePerc', y = 'walkDistance', data = origin_data, size=8, ratio = 3, color = 'g')
plt.show()

print("{} players have won without a single kill!".format(
      len(origin_data[origin_data['winPlacePerc']==1])
     )
data_damage_0 = origin_data[origin_data['damageDealt'] == 0].copy()
print("{} players have won without dealing damage!".format(
    len(data_damage_0[data_damage_0['winPlacePerc']==1])
     )

127573 players have won without a single kill!
4770 players have won without dealing damage!

另外，点图代表散点图位置的数值变量的中心趋势估计，并使用误差线提供关于该估计的不确定性的一些指示。点图可能比条形图更有用于聚焦一个或多个分类变量的不同级别之间的比较。

下图为毁坏交通工具数量与最终排名之间的关系：

f,ax1 = plt.subplots(figsize =(10,6))
sns.pointplot(x = 'vehicleDestroys', y = 'winPlacePerc', data = origin_data, color='#606060', alpha=0.8)
plt.xlabel('Number of Vehicle Destroys',fontsize = 15,color='blue')
plt.ylabel('Win Percentage',fontsize = 15,color='blue')
plt.title('Vehicle Destroys/ Win Ratio',fontsize = 20,color='blue')
plt.grid()
plt.show()

可见毁坏过交通工具的玩家比没有毁坏过交通工具的玩家的最终排名靠前，毁坏越多排名越前（额。本吃鸡菜鸟也没想通这是为什么。很暴力hh。）
还可以分几个类别来看最终排名与击杀敌人的数量的对比：

## teamKills击杀队友数
#print origin_data['teamKills'].value_counts()
origin_data['teamKills_rank'] = pd.cut(origin_data['teamKills'], [-1, 0, 13] 
 ,labels = ['No TeamKills', 'Kill Teammates'])
f,ax1 = plt.subplots(figsize =(10,6))
sns.pointplot(x = 'kills_rank', y = 'winPlacePerc', data = origin_data, hue = 'teamKills_rank')
#dodge=True可以使重叠的部分错开

headshotKills为爆头击杀敌人数量，区分是否有过爆头击杀来看击杀敌人数量与最终得分的关系：

#print origin_data['headshotKills'].value_counts() #最大值为64
origin_data['headshotKills_rank'] = pd.cut(origin_data['headshotKills'], [-1, 0, 65] ,labels = ['No headshotKills', 'Did headshotKills'])
f,ax1 = plt.subplots(figsize =(10,6))
sns.pointplot(x = 'kills_rank', y = 'winPlacePerc', data = origin_data, hue = 'headshotKills_rank')

基本上，在相同击杀数的情况下，有过爆头的玩家的得分会略高于没有过爆头的玩家的数量。

Heal和boost与最终得分的关系：

new_data = origin_data.copy()
new_data = new_data[new_data['heals'] < new_data['heals'].quantile(0.99)]
new_data = new_data[new_data['boosts'] < new_data['boosts'].quantile(0.99)]
f, ax1 = plt.subplots(figsize = (10, 6))
sns.pointplot(x = 'heals', y = 'winPlacePerc', data = new_data, color = 'lime', alpha = 0.8)
sns.pointplot(x = 'boosts', y = 'winPlacePerc', data = new_data, color = 'blue', alpha = 0.8)
plt.text(5, 0.45, 'Heals', color = 'lime', style = 'italic')
plt.text(5, 0.5, 'Boosts', color = 'blue', style = 'italic')
plt.xlabel('Number of heal/boost items',fontsize = 15,color='blue')
plt.ylabel('Win Percentage',fontsize = 15,color='blue')
plt.title('Heals vs Boosts',fontsize = 20,color='blue')
plt.grid()
plt.show()
del new_data

使用提升性物品（boosts）会提高最终排名；
使用4个以下治疗性物品（救援包等）时，使用越多救援包的人最终排名越靠前，而但使用过多的救援包并不会一直提高最终排名，达到3-4个救援包时排名不再提升。

下面，区分不同的组局方式/匹配方式，来看各方式下的最终排名与各个变量之间的关系

一局的队伍数如果大于50，认为是单排solos
队伍数在25到50之间，认为是双排duos
队伍数小于等于25，认为是四排squads

solos = origin_data[origin_data['numGroups']>50]
duos = origin_data[(origin_data['numGroups']>25) & (origin_data['numGroups']<=50)]
squads = origin_data[origin_data['numGroups']<=25]
print("There are {} ({:.2f}%) solo games, {} ({:.2f}%) duo games and {} ({:.2f}%) squad games."
      .format(len(solos), 
              100*len(solos)/len(origin_data), 
              len(duos), 
              100*len(duos)/len(origin_data), 
              len(squads), 
              100*len(squads)/len(origin_data)
             )
     )

There are 709111 (15.00%) solo games, 3295326 (74.00%) duo games and 442529 (9.00%) squad games.

各方式下的最终排名与击杀敌人数量之间的关系：

f,ax1 = plt.subplots(figsize =(20,10))
sns.pointplot(x='kills',y='winPlacePerc',data=solos,color='black',alpha=0.8)
sns.pointplot(x='kills',y='winPlacePerc',data=duos,color='#CC0000',alpha=0.8)
sns.pointplot(x='kills',y='winPlacePerc',data=squads,color='#3399FF',alpha=0.8)
plt.text(37,0.6,'Solos',color='black',fontsize = 17,style = 'italic')
plt.text(37,0.55,'Duos',color='#CC0000',fontsize = 17,style = 'italic')
plt.text(37,0.5,'Squads',color='#3399FF',fontsize = 17,style = 'italic')
plt.xlabel('Number of kills',fontsize = 15,color='blue')
plt.ylabel('Win Percentage',fontsize = 15,color='blue')
plt.title('Solo vs Duo vs Squad Kills',fontsize = 20,color='blue')
plt.grid()
plt.show()

上图所示，单排的局，最终排名随着击杀数量的增加而增加的趋势更快（击杀量过高要么天选要么开挂了。。暂不考虑，只考虑击杀量在正常范围内的情况，比如30以内），双排次之，四排的局最终排名随着击杀数量的增加而增加的趋势相对较缓。另外，单排和双排的局，在击杀量到达7个以上时，就能基本在前10%了（平均得分place在0.9以上），而四排的局，在击杀量到7之前，排名随击杀量的提升而稳步提升，而在击杀量到7以后，排名与击杀量的关系不稳定了起来。

下面是最终排名与击倒敌人的数量、伤害敌人（最终被队友击杀）的数量、救援队友的数量之间的关系：

f,ax1 = plt.subplots(figsize =(20,10))
sns.pointplot(x='DBNOs',y='winPlacePerc',data=duos,color='#CC0000',alpha=0.8)
sns.pointplot(x='DBNOs',y='winPlacePerc',data=squads,color='#3399FF',alpha=0.8)
sns.pointplot(x='assists',y='winPlacePerc',data=duos,color='#FF6666',alpha=0.8)
sns.pointplot(x='assists',y='winPlacePerc',data=squads,color='#CCE5FF',alpha=0.8)
sns.pointplot(x='revives',y='winPlacePerc',data=duos,color='#660000',alpha=0.8)
sns.pointplot(x='revives',y='winPlacePerc',data=squads,color='#000066',alpha=0.8)
plt.text(14,0.5,'Duos - Assists',color='#FF6666',fontsize = 12,style = 'italic')
plt.text(14,0.45,'Duos - DBNOs',color='#CC0000',fontsize = 12,style = 'italic')
plt.text(14,0.4,'Duos - Revives',color='#660000',fontsize = 12,style = 'italic')
plt.text(14,0.35,'Squads - Assists',color='#CCE5FF',fontsize = 12,style = 'italic')
plt.text(14,0.3,'Squads - DBNOs',color='#3399FF',fontsize = 12,style = 'italic')
plt.text(14,0.25,'Squads - Revives',color='#000066',fontsize = 12,style = 'italic')
plt.xlabel('Number of DBNOs/Assits/Revives',fontsize = 10,color='blue')
plt.ylabel('Win Percentage',fontsize = 10,color='blue')
plt.title('Duo vs Squad DBNOs, Assists, and Revives',fontsize = 15,color='blue')
plt.grid()
plt.show()
del solos
del duos
del squads

3、探索性分析——多个变量(heatmap+pairplot)

热力图部分参数的含义：

• cmap:从数字到色彩空间的映射，取值是matplotlib包里的colormap名称或颜色对象，或者表示颜色的列表；改参数默认值：根据center参数设定

• center:数据表取值有差异时，设置热力图的色彩中心对齐值；通过设置center值，可以调整生成的图像颜色的整体深浅；设置center数据时，如果有数据溢出，则手动设置的vmax、vmin会自动改变

• annot(annotate的缩写):默认取值False；如果是True，在热力图每个方格写入数据；如果是矩阵，在热力图每个方格写入该矩阵对应位置数据

• square:设置热力图矩阵小块形状，默认值是False

• fmt:字符串格式代码，矩阵上标识数字的数据格式，比如保留小数点后几位数字

• annot_kws:默认取值False；如果是True，设置热力图矩阵上数字的大小颜色字体，matplotlib包text类下的字体设置；

• cbar:是否在热力图侧边绘制颜色刻度条，默认值是True

• cbar_kws:热力图侧边绘制颜色刻度条时，相关字体设置，默认值是None

• cbar_ax:热力图侧边绘制颜色刻度条时，刻度条位置设置，默认值是None

• xticklabels, yticklabels:xticklabels控制每列标签名的输出；yticklabels控制每行标签名的输出。默认值是auto。如果是True，则以DataFrame的列名作为标签名。如果是False，则不添加行标签名。如果是列表，则标签名改为列表中给的内容。如果是整数K，则在图上每隔K个标签进行一次标注。如果是auto，则自动选择标签的标注间距，将标签名不重叠的部分(或全部)输出

下面使用origin_data.corr()获得包含全部变量两两关系的相关系数矩阵
只取其中k个与因变量相关性最大的变量，作出其热力图

k = 10
cols = origin_data.corr().nlargest(k, 'winPlacePerc')['winPlacePerc'].index[1:k]
k_corr = np.corrcoef(origin_data[cols].values.T)
sns.set(font_scale=1.25)
f,ax = plt.subplots(figsize=(15, 15))
sns.heatmap(k_corr, cbar = True, annot = True, square = True, fmt = '.2f', center =0.6
           ,annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

pairplot图

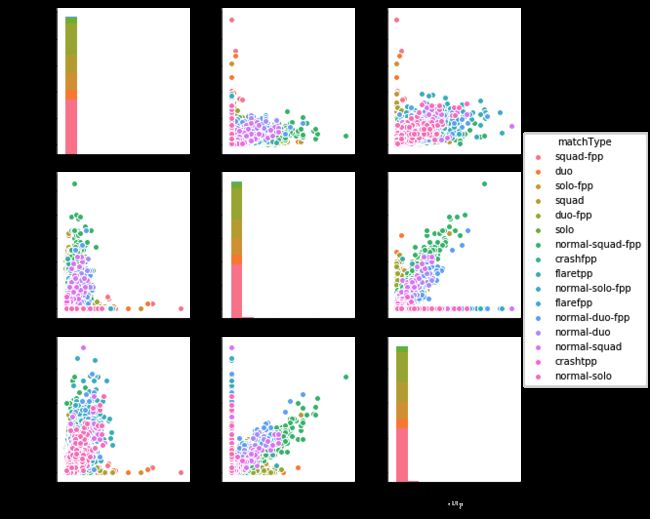
new_data = origin_data.loc[:,['weaponsAcquired','DBNOs','kills','matchType']]
sns.pairplot(new_data,hue='matchType')

new_data_0 = origin_data.loc[:,['DBNOs','heals','boosts','walkDistance']]
sns.pairplot(new_data_0)

注：

本文大部分的图的画法来源于Dimitrios Effrosynidis的分享
欢迎指正