[论文笔记] Universal Adversarial Perturbations Against Semantic Image Segmentation(ICCV 2017)

Universal Adversarial Perturbations Against Semantic Image Segmentation(ICCV 2017)

• 文章简介:
  • DataSet: Cityscapes
  • 区别: 与普通的单目标图片分类相比，多目标的语义分割任务会存在一个问题，就是某些target像素点的梯度方向可能正好与另外target像素点的梯度方向相反。而一般的交叉熵损失函数会鼓励已经正确预测的目标结果朝着更高的置信度发展，从而减少损失。面对不同目标之间的竞争，这未必是可取的。因此，为了解决这个问题，作者设置了一个置信度阈值$\tau =0.75$, 即超过这个阈值就认为是目标像素点，置信度即使继续提高也不会减少损失(文中没有明说，但我觉得是这个意思)
  • 特点: 生成universal扰动时不需要用到ground-truth标签

本文主要研究的是semantic image segmentation方面的universal攻击.

下图是static target segmentations: 即输出的语义分割结果与输入无关。

下图是dynamic target segmentation: 只移除某些object的分割结果，而保持其他不变

• Contribution:

  • 证明了targeted universal扰动可以存在于semantic image segmentaion任务中
  • 提出了2种生成扰动的高效方法
    • 目标是让网络产生一个固定的target segmentaion结果
    • 目标是让segmentaion结果只删除部分target class而其他保持不变
  • 发现产生的universal扰动与预测结果的结构很相似
  

• Segmentation:
  

  • Static target segmentation：
    
    在这种场景下，攻击者的目标是固定分割结果，如将$t_0$时刻分割结果固定住，后面时刻$t$要满足下式
    $$y_t^{target}=y_{t_0}^{pred}\forall t>t_0$$
      他的攻击对象是static camera(不太懂摄影，可能指那种每隔一段时间就拍一下照类似于红绿灯拍照吧?)，希望能够隐藏一段时间内的活动变化。
  • Dynamic target segmentation：
    
    这个场景考虑ego-motion(帧间运动)，因为static target segmentation不适用于考虑场景的变化造成的移动相机。他的目标是：移除某些类别的分割结果，而其他保持不变。其中想要去隐藏的目标类为$o$, 并令
    $${\mathcal{I}}_o=\{(i,j)|f_{\theta }(x_{ij})=o\}$$
      因此背景就为
    $${\mathcal{I}}_{bg}=\mathcal{I}\backslash {\mathcal{I}}_o$$
      然后采用一个启发式的最近邻思想，将想要隐藏的目标预测结果置为附近最近的背景的预测结果，即
    $$y_{ij}^{target}=y_{i^{\prime }{j}^{\prime }}^{pred}\forall (i,j)\in {\mathcal{I}}_o$$
      其中$i^{\prime }$和$j^{\prime }$的选择为
    $$i^{\prime },j^{\prime }=\underset{i^{\prime },j^{\prime }\in {\mathcal{I}}_{bg}}{\mathrm{argmin}}(i^{\prime }-i{)}^2+(j^{\prime }-j{)}^2$$

• $y^{target}$的选择
  
  作者并没有直接基于ground-truth $y^{true}$来选择$y^{target}$，因为对于对抗样本而言，并不知道ground-truth。所以作者最终是基于$y^{pred}$来生成的(即使是黑盒攻击，也能获取到预测值)

• Image-Dependent Perturbations(注意不同于universal扰动，他只有一个tile)
  
  对语义分割任务，它的损失函数通常为：

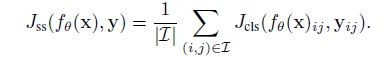
  因此，在攻击时，目标就是去寻找对抗样本$x^{adv}$，从而
$$\arg \min J_{ss}(f_{\theta }(x^{adv},y^{target}))$$
  不过文章中采用另一种方案：
$$J_{ss}^{\omega }(f_{\theta }(x),y^{target})=\frac{1}{|\mathcal{I}|}\{\omega \sum _{(i,j)\in {\mathcal{I}}_o}{J}_{cls}(f_{\theta }(x{)}_{i,j},y_{ij}^{target})+(1-\omega )\sum _{(i,j)\in {\mathcal{I}}_{bg}}{J}_{cls}(f_{\theta }(x{)}_{i,j},y_{i,j}^{target})\}$$
  当$\omega =1$该函数值关注于将目标类移除，当$\omega =0$时，该函数只保持背景不变，所以在这个函数中$y^{target}$应该是指背景。

• Universal Perturbations(用相同的tile铺满):
  
  作者在这边设计universal扰动时时基于上面的Image-Dependent Perturbations:

  然后迭代过程为:

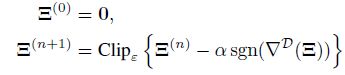
  不过这样处理的潜在问题在于可能会导致扰动过拟合，事实上，这是很容易存在的问题，因为扰动的维度与输入图像一致，非常高。于是作者换了一种方式:

  于是对于所有的$i,j\in \mathcal{I}$,增加一个限制
$${\Xi }_{i,j}={\Xi }_{i+h,j}{\Xi }_{i,j}={\Xi }_{i,j+w}$$
  这样一来，只要优化一个大小为[h,w]的tile扰动，然后将它铺满整个$\Xi$就行了

  下式中的$R$和$S$表示tiles在height和width维度上的个数, 且
$$[r,s]=\{i,j|[rh\le i<(r+1)h]\bigwedge [sw\le j<(s+1)w\}$$

• Result:
  
  对于不同$ϵ$，可以发现static target segmentation在训练集和验证集上的结果十分接近，同时也证明了在高维空间中，过拟合也不是一个无法处理的问题。不过这可能也归功于：大量的训练集和一致的target

  不同tile size的比较:

  1. 黑色的曲线(No periodicity)值得是universal但是只有1个tile(即扰动的size正好与原图相同)的结果

  2. 蓝色五角星(image-dependent)是一张图片一个扰动的结果，并且也是只有1个tile

  3. 剩下的就是不止一个tile的universal结果，可以发现tile的size增大能提高背景像素点的保留比但是需要牺牲行人隐藏率。

---

如果觉得我有地方讲的不好的或者有错误的欢迎给我留言，谢谢大家阅读（点个赞我可是会很开心的哦）~