【量化投资】基金择时策略浅析(3) -实用择时方法
常见择时方法
本系列第一篇文章中曾介绍过选品和择时的概念,并且提到过这两个其实都是定义比较宽松的概念,任何投资者在任何市场中做的投资决策,无论是依据基本面因素,技术指标,还是量化模型,都可以看作择时。由于本文所针对的是中长期基金投资,所以这里讨论的择时方法带有更明确的目的:即判断整个股票市场目前的走势方向/热度/牛熊,因此本文涉及的择时方法都是中长期的技术类方法。
a) 自下而上的方法
自下而上的方法判断市场走向,就是要从市场中的每个成分入手,通过市场中每个成分股的状态来判断市场总体的状态。这种方法适用于对全市场或者某个细分市场/指数的走势进行判断。这种分析方法的一般流程如下:
自下而上的方法需要的输入变量包括成分股集合S,个股指标f,个股判断条件t,总体指标F,总体判断条件T,那么此方法可以一般化表示为F(S,f,t)>T,其中指标值F可用于输出连续型结果,F>T可用来输出分类型结果。
自下而上方法的具体实现主要依赖于如何选择f和t,一般来说,用来判断个股趋势的各类技术指标都可以作为f使用,t只要保证与f配套即可。下面我们用一个具体的例子来演示指标计算过程和效果。
为了验证上述择时方法有效性,我们进一步根据输出F>T构建了一个简单的交易策略,即当F>T的时候买入,当F
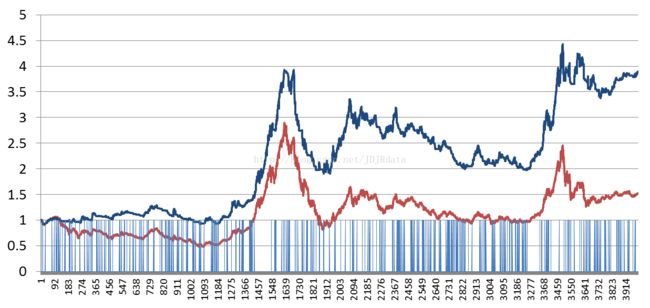
图1:自下而上的择时交易策略与大盘指数对比
图1中下方的蓝色竖线表示的是入场时点,在整个回测的17年中,该策略入场次数达330次,因此如果将上述方法应用于基金投资,那么交易成本的影响将会是显著的。从这个角度来看,该策略(或者策略参数的选择)并不能满足基金投资的中长操作周期,它的操作信号过于频繁。
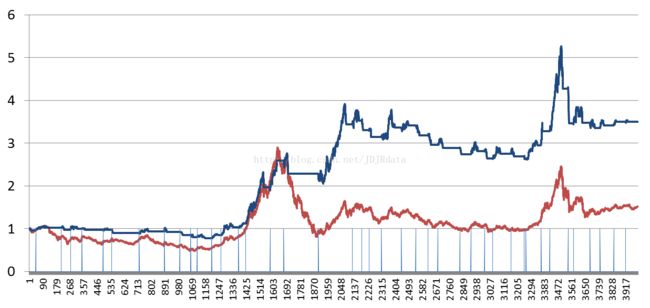
对于这个策略来说,降低操作频率只需要对参数进行微调,例如可以将原策略T=0.5调整为T=(0.4,0.6),当F>0.6时判断为牛市,如果此时为空仓则买入,当F<0.4 的时候判断为熊市,如果此时满仓则卖出,0.4~0.6之间作为操作弹性空间,图2显示了调整参数后的结果,虽然整体净值下降到3.5,但操作次数下降为41次,考虑交易成本之后的表现应该比T=0.5强不少。
图2:调整参数后的自下而上的择时策略
b) 直接技术指标
相比自下而上的择时方法,使用单一技术指标直接对大盘指数或者投资标的行情曲线进行分析是更直接更容易操作的方法。这种方法对任何能获取到行情曲线的资产都可以使用,无论是指数,基金,还是股票。用于判断趋势的常用技术指标有很多,这类指标的共同点是滞后性,即在趋势出现一段时间之后才给出信号,因此使用这类指标进行交易也常被称作(底部)右侧交易。
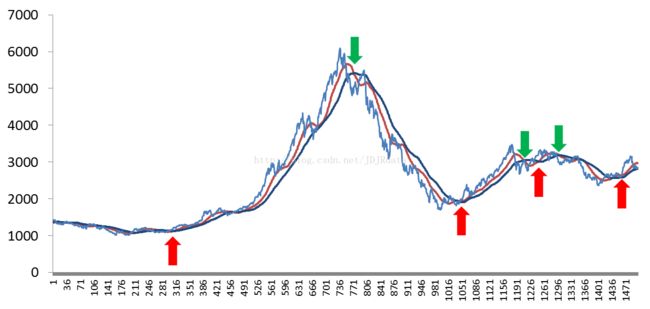
图3是以双均线系统作为择时方法对上证指数进行操作的回测结果,策略参数使用指数收盘价的35日和70日移动平均线,将35日均线向上穿越70日均线作为牛市开始的信号(买入),将35日均线向下穿越70日均线作为熊市开始的信号(卖出)(参见图4,红色箭头为买入信号,绿色为卖出信号)。该策略在回测的17年中共发生28次入场,期末净值达到7,年化收益率约为12.7%。
图3:双均线策略的回测净值曲线
图4:双均线系统原理示意
相比于自下而上的例子,直接对上证指数应用双均线系统得到的策略更接近基金中长期投资的操作方式,操作频率更低并且收益更高些。从净值曲线上能明显看出有多个空仓的区间(净值曲线水平无波动的部分),这些时间段大都处在指数下跌的过程中,因此该策略的择时效果是比较明显的。
择时方法的比较
自下而上的方法适用于能够准确获得成分股的大盘或细分市场指数,具体应用的情景一般有两种:1)通过对全市场股票的分析得到整个市场的运行状态,然后将这个全局状态作为一个变量输入到具体的投资模型中,或者用这个状态来指导股票投资或股票型基金投资的仓位;2)通过对细分市场指数成分股的分析得到细分市场的运行状态,然后用这个状态直接决定对该细分市场指数基金的操作。这两种情景的差异在于,第2种情景里自下而上分析的对象就是投资标的本身,而第1种情景中分析的是全市场,投资标的可以是任何相关的资产。
直接技术指标的应用范围则更广一些,它还可以用来分析基础资产(无成分)或者非指数基金(成分不确定),操作上也要更简单一些。
在第1种情景下,自下而上的方法由于平等考虑了每个股票的状态,因此它能够更准确的表达市场的热度信息。直接使用单一技术指标来对大盘指数进行分析则会受到指数成分取样以及成分权重带来的干扰,即指数不是总能反映真实的市场状态,尤其是在极端行情下。而在第2种情景下,直接技术指标的使用会更便捷和容易把握。
需要注意的是,这两种方法都是滞后的,仅适用于特定的市场环境。细心的读者会发现,尽管上面例子的总收益很好,但是这些收益大都来自于两轮大牛市。在长期盘整或熊市中,策略会有多次错误入场,这使得净值遭受损失。
结语
a) 上述方法都是基于有滞后性的技术指标,策略的收益主要来自于大牛市以及牛市之后的正确离场。在不存在大牛市的市场中,这样的策略将会因为频繁的错误入场而失效。
b) 这些策略的短期回撤幅度仍然较大,因此必须长期执行才能获得正的期望收益。
c) 在股票市场的建模过程中,样本数据是相对稀缺,因此模型的稳定性比参数最优化更重要。文中例子的参数并未经过充分优化,然而这并不影响它们的有效性和实用性。在本系列的下一篇中我们会讨论这几个例子中的参数优化和模型稳定性等问题。