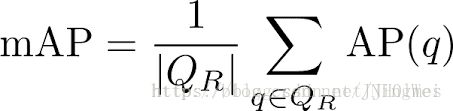Recall_Precision_mAP
召回率(Recall),精确率(Precision),平均正确率(Average_precision(AP) ),交除并(Intersection-over-Union(IoU))
Accuracy:准确率,预测对的除以总样本数
Precision:准确率/预测正率 (正样本)
Recall :召回率/查对率,预测对占实际是对的
mAP
公式
多标签图像分类(Multi-label Image Classification)任务中图片的标签不止一个,因此评价不能用普通单标签图像分类的标准,即mean accuracy。该任务采用的是和信息检索中类似的方法—mAP(mean Average Precision)。mAP虽然字面意思和mean accuracy看起来差不多,但是计算方法要繁琐得多。
在图像中,尤其是分类问题中,AP是一种评价ranking方式好不好的指标:
举例来说,一个二分类问题,分别5个样本,如果这个分类器性能达到完美的话,ranking结果应该是:
+1,+1,+1,+1,+1,-1,-1,-1,-1,-1
但是分类器预测的label,和实际的score肯定不会这么完美。这个过程为:首先把所有bbox找出,并在上面加上confidence,每一类都根据confidence从大到小排列,接下来计算两个指标:precision和recall。比如分类器认为打分由高到低选择了前四个,实际上这里面只有两个是正样本。此时的recall就是2(能包住的正样本数)/5(总共的正样本数)=0.4,precision是2(你选对了的)/4(总共选的)=0.5
从上面的例子可以看出,其实precision,recall都是选多少个样本k的函数,如果总共有1000个样本,那么就可以像这样计算1000对P-R,并把他们画出来,这就是PR曲线。
这里有一个趋势,recall越高,precision越低。这是很合理的,从公式中可以看出,虽然精确率与召回率没有必然的关系,然而在大规模数据集合中,这两个指标却是相互制约的。由于“检测策略”并不完美,当希望检测到更多相关对象时,放宽检测策略,往往也会伴随出现一些不相关的结果,从而使准确率受到影响;当希望去除检测结果中的不相关对象时,将检测策略定的更加严格,这样也会使有一些相关的对象不再能被检测到,从而使召回率受到影响。由于两个指标相互制约,必须根据需要为检测策略选择一个合适的度,不能太严格也不能太松,寻求在召回率和精确率中间的一个平衡点。
mAP,mean average precision,其中的AP就是这个曲线下的面积,average是对recall取平均,mean是对所有类别取平均(每一个类当做一次二分类任务)。
VOC08之后AP11已经被抛弃了。貌似从VOC08之后要求PR曲线必须单调下降了?这个不太确定。
1.使用AP会比accuracy要合理。对于accuracy,如果有9个负样本和一个正样本,那么即使分类器什么都不做全部判定为负样本accuracy也有90%。但是对于AP,recall=1那个点precision会掉到0.1.曲线下面积就会反映出来。
2.在实际中计算AP时,如果是matlab的话,可以直接调用vl_feat中的vl_pr:VLFeat - Tutorials这里面详细地给出了概念的解释以及计算方式。
例1:
例2:
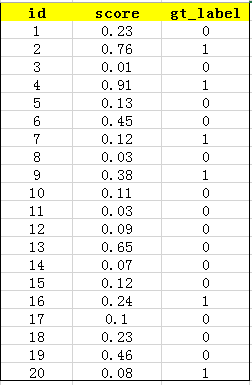
首先用训练好的模型得到所有测试样本的confidence score,每一类(如car)的confidence score保存到一个文件中(如comp1_cls_test_car.txt)。假设共有20个测试样本,每个的id,confidence score和ground truth label如下:
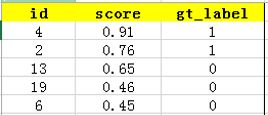
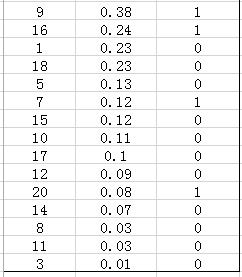
接下来对confidence score排序,得到:
这张表很重要,接下来的precision和recall都是依照这个表计算的
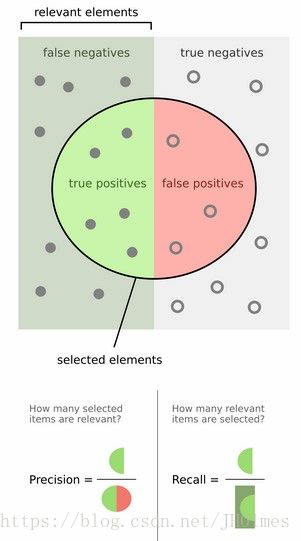
然后计算precision和recall,这两个标准的定义如下:
上图比较直观,圆圈内(true positives + false positives)是我们选出的元素,它对应于分类任务中我们取出的结果,比如对测试样本在训练好的car模型上分类,我们想得到top-5的结果,即:
在这个例子中,true positives就是指第4和第2张图片,false positives就是指第13,19,6张图片。方框内圆圈外的元素(false negatives和true negatives)是相对于方框内的元素而言,在这个例子中,是指confidence score排在top-5之外的元素,即:
其中,false negatives是指第9,16,7,20张图片,true negatives是指第1,18,5,15,10,17,12,14,8,11,3张图片。
那么,这个例子中Precision=2/5=40%,意思是对于car这一类别,我们选定了5个样本,其中正确的有2个,即准确率为40%;Recall=2/6=30%,意思是在所有测试样本中,共有6个car,但是因为我们只召回了2个,所以召回率为30%。
实际多类别分类任务中,我们通常不满足只通过top-5来衡量一个模型的好坏,而是需要知道从top-1到top-N(N是所有测试样本个数,本文中为20)对应的precision和recall。显然随着我们选定的样本越来也多,recall一定会越来越高,而precision整体上会呈下降趋势。把recall当成横坐标,precision当成纵坐标,即可得到常用的precision-recall曲线。这个例子的precision-recall曲线如下:
接下来说说AP的计算,此处参考的是PASCAL VOC CHALLENGE的计算方法。首先设定一组阈值,[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值(比如recall>0.3),我们都会得到一个对应的最大precision。这样,我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。
当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这N个样本中有M个正例,那么我们会得到M个recall值(1/M, 2/M, ..., M/M),对于每个recall值r,我们可以计算出对应(r' > r)的最大precision,然后对这M个precision值取平均即得到最后的AP值。计算方法如下:
相应的Precision-Recall曲线(这条曲线是单调递减的)如下:
AP衡量的是学出来的模型在每个类别上的好坏,mAP衡量的是学出的模型在所有类别上的好坏,得到AP后mAP的计算就变得很简单了,就是取所有AP的平均值。
代码
#PASCAL VOC评价Detection结果的代码
def voc_ap(self, rec, prec, use_07_metric=True):
if use_07_metric:
ap = 0.
# 2010年以前按recall等间隔取11个不同点处的精度值做平均(0., 0.1, 0.2, …, 0.9, 1.0)
for t in np.arange(0., 1.1, 0.1):
if np.sum(rec >= t) == 0:
p = 0
else:
# 取最大值等价于2010以后先计算包络线的操作,保证precise非减
p = np.max(prec[rec >= t])
ap = ap + p / 11.
else:
# 2010年以后取所有不同的recall对应的点处的精度值做平均
# first append sentinel values at the end
mrec = np.concatenate(([0.], rec, [1.]))
mpre = np.concatenate(([0.], prec, [0.]))
# 计算包络线,从后往前取最大保证precise非减
for i in range(mpre.size - 1, 0, -1):
mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
# 找出所有检测结果中recall不同的点
i = np.where(mrec[1:] != mrec[:-1])[0]
# and sum (\Delta recall) * prec
# 用recall的间隔对精度作加权平均
ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
return ap
# 计算每个类别对应的AP,mAP是所有类别AP的平均值
def voc_eval(self, detpath,
classname,
ovthresh=0.5,
use_07_metric=True):
# 提取所有测试图片中当前类别所对应的所有ground_truth
class_recs = {}
npos = 0
# 遍历所有测试图片
for imagename in imagenames:
# 找出所有当前类别对应的object
R = [obj for obj in recs[imagename] if obj['name'] == classname]
# 该图片中该类别对应的所有bbox
bbox = np.array([x['bbox'] for x in R])
difficult = np.array([x['difficult'] for x in R]).astype(np.bool)
# 该图片中该类别对应的所有bbox的是否已被匹配的标志位
det = [False] * len(R)
# 累计所有图片中的该类别目标的总数,不算diffcult
npos = npos + sum(~difficult)
class_recs[imagename] = {'bbox': bbox,
'difficult': difficult,
'det': det}
# 读取相应类别的检测结果文件,每一行对应一个检测目标
if any(lines) == 1:
# 某一行对应的检测目标所属的图像名
image_ids = [x[0] for x in splitlines]
# 读取该目标对应的置信度
confidence = np.array([float(x[1]) for x in splitlines])
# 读取该目标对应的bbox
BB = np.array([[float(z) for z in x[2:]] for x in splitlines])
# 将该类别的检测结果按照置信度大小降序排列
sorted_ind = np.argsort(-confidence)
sorted_scores = np.sort(-confidence)
BB = BB[sorted_ind, :]
image_ids = [image_ids[x] for x in sorted_ind]
# 该类别检测结果的总数(所有检测出的bbox的数目)
nd = len(image_ids)
# 用于标记每个检测结果是tp还是fp
tp = np.zeros(nd)
fp = np.zeros(nd)
# 按置信度遍历每个检测结果
for d in range(nd):
# 取出该条检测结果所属图片中的所有ground truth
R = class_recs[image_ids[d]]
bb = BB[d, :].astype(float)
ovmax = -np.inf
BBGT = R['bbox'].astype(float)
# 计算与该图片中所有ground truth的最大重叠度
if BBGT.size > 0:
......
overlaps = inters / uni
ovmax = np.max(overlaps)
jmax = np.argmax(overlaps)
# 如果最大的重叠度大于一定的阈值
if ovmax > ovthresh:
# 如果最大重叠度对应的ground truth为difficult就忽略
if not R['difficult'][jmax]:
# 如果对应的最大重叠度的ground truth以前没被匹配过则匹配成功,即tp
if not R['det'][jmax]:
tp[d] = 1.
R['det'][jmax] = 1
# 若之前有置信度更高的检测结果匹配过这个ground truth,则此次检测结果为fp
else:
fp[d] = 1.
# 该图片中没有对应类别的目标ground truth或者与所有ground truth重叠度都小于阈值
else:
fp[d] = 1.
# 按置信度取不同数量检测结果时的累计fp和tp
# np.cumsum([1, 2, 3, 4]) -> [1, 3, 6, 10]
fp = np.cumsum(fp)
tp = np.cumsum(tp)
# 召回率为占所有真实目标数量的比例,非减的,注意npos本身就排除了difficult,因此npos=tp+fn
rec = tp / float(npos)
# 精度为取的所有检测结果中tp的比例
prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)
# 计算recall-precise曲线下面积(严格来说并不是面积)
ap = self.voc_ap(rec, prec, use_07_metric)
# 如果这个类别对应的检测结果为空,那么都是-1
else:
rec = -1.
prec = -1.
ap = -1.
return rec, prec, ap