python OpenCV学习笔记（十七）：轮廓特征

官方文档 – https://docs.opencv.org/3.4.0/dd/d49/tutorial_py_contour_features.html

---

Image moments帮助你计算一些特征比如物体的质心，物体的面积等等。详见：Image Moments
cv.moments(array[, binaryImage])

import numpy as np
import cv2 as cv

img = cv.imread('star.jpg', 0)
ret, thresh = cv.threshold(img, 127, 255, 0)
im2, contours, hierarchy = cv.findContours(thresh, 1, 2)

cnt = contours[0]
M = cv.moments(cnt)
print M

通过得出的moments，你可以提取出有用的数据，如面积、中心id等。以下可以计算出中心坐标：

cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])

轮廓面积

轮廓面积可以通过cv.contourArea()方法，或者从moments的M['m00']获取

area = cv.contourArea(cnt)

cv.contourArea(contour[, oriented])

轮廓周长

它也被称为弧长。可以使用cv.arcLength()函数找到它。第二个参数指定形状是否是一个封闭的轮廓(如果是正确的)，或者只是一个曲线。

perimeter = cv.arcLength(cnt,True)

cv.arcLength(curve, closed)

轮廓近似

cv.approxPolyDP(curve, epsilon, closed[, approxCurve])
它近似于一个轮廓形状到另一个形状，它的顶点数量较少，这取决于我们所指定的精度。
假设您想要在图像中找到一个正方形，但是由于图像中的一些问题，您并没有得到一个完美的正方形，而是一个“糟糕的形状”(如下图所示)。现在你可以用这个函数来近似它的形状。第二个参数叫做epsilon，它是从轮廓到近似轮廓的最大距离。它是一个精确的参数。为了得到正确的输出，需要明智地选择epsilon。

epsilon = 0.1 * arcLength(cnt, True)
approx = cv.approxPolyDP(cnt, epsilon, True)

在第二幅图中，绿线显示了epsilon=10%的弧长曲线。第三张图显示的是弧长的1%。第三个参数规定了曲线是否闭合。

凸包

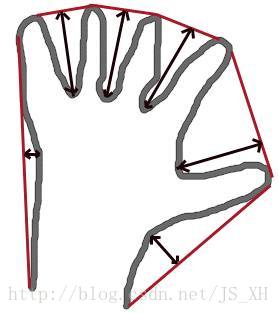
凸包看起来类似于轮廓近似，但它不是(两者在某些情况下可能提供相同的结果)。cv.convexHull()检查凸性缺陷的曲线，并修正它。一般来说，凸曲线是凸出来的曲线，或者至少是平坦的。如果它向内膨胀，就叫做凸性缺陷。例如，检查下面的手的图像。红线显示的是手的凸包（convex hull）。双侧箭头表示凸性缺陷，即外壳（hull）与轮廓的局部最大偏差。

hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]])
points：传入的轮廓
hull：输出，通常不传
clockwise：定位标志。如果是正确的，输出凸壳是顺时针方向的。否则，它是逆时针方向的。
returnPoints：默认情况下为真。返回hull的坐标。如果为假，它会返回与hull点对应的轮廓点的索引。
所以，要得到上图的凸包：

hull = cv.convexHull(cnt)

但是如果你想找到凸性缺陷，你需要传入returnPoints=False。为了理解它，我们将使用上面的矩形图像。首先，我发现它的轮廓是cnt。现在我找到了它的凸包，它的returnPoints=True，我得到了以下值:：[[[234 202]]，[[ 51 202]]，[[ 51 79]]，[[234 79]]] ，这是矩形的四个角点。现在如果同样的returnPoints=False，我得到以下结果：[[129]，[ 67]，[ 0]，[142]]。这些是轮廓坐标对应的轮廓点的索引。例如，第一个值：cnt[129]=[[234 202]]，这与第一个结果相同(对于其他的结果也是如此)。

检查凸性

cv.isContourConvex(contour)可以检查曲线是否为凸形，它只是返回是否为真或假。

k = cv.isContourConvex(cnt)

边界矩形

边界矩形有两种

直边界矩形

它是一个直的矩形，它不考虑物体的旋转。所以矩形的面积不会是最小的。可以使用函数cv.boundingRect(points)。
（x，y）为矩形的左上角坐标，（w，h）是它的宽和高。

x, y, w, h = cv.boundingRect(cnt)
cv.rectangle(img, (x,y), (x+w,y+h), (0,255,0), 2)

旋转边界矩形

使用函数cv.minAreaRect(points)，边界矩形是用最小面积绘制的，因此它也考虑了旋转。它返回一个Box2D结构，其中包含以下的信息：中心坐标(x，y)，(宽度，高度)，旋转角度)。但是要画出这个矩形，我们需要矩形的4个角。由cv.boxPoints(box[, points])函数获得。

rect = cv.minAreaRec(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img, [box], 0, (0,0,255), 2)

两个矩形都显示在一个单独的图像中。绿色矩形显示的是正常的边界矩形。红色矩形是旋转的矩形。

最小闭合圆

cv.minEnclosingCircle(points)方法，一个完全覆盖了物体的最小面积的圆周。

(x, y), radius = cv.minEnclosingCircle(cnt)
center = (int(x), int(y))
radius = int(radius)
cv.circle(img, center, radius, (0,255,0), 2)

拟合椭圆

将一个椭圆与一个物体匹配。返回旋转矩形的内接椭圆。

ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),2)

拟合直线

一条线与一组点相匹配。下图包含一组白点。我们可以给出一条近似直线。详见 cv.fitLine

rows, cols = img.shape[:2]
[vx, vy, x, y] = cv.fitLine(cnt, cv.DIST_L2, 0, 0.01, 0.01)
lefty = int((-x * vy/vx) + y)
righty = int(((cols-x) * vy/vx) + y)
cv.line(img, (cols-1, righty), (0, lefty), (0,255,0), 2)

cv.fitLine(points, distType, param, reps, aeps[, line])