计算机图形学基础 : 基本图形生成算法之直线的扫描转换

学习了三种常用的直线扫描转换算法 ：数值微分法(DDA)、中点画线法和Bresenham画线算法.

注 : 本文中的程序都是假定斜率在0~1之间，其他斜率类似，做相应的简单处理就好。

数值微分法(DDA,  Digital Differential Analyzer)

直线扫描转换最简单的方法是先算出直线的斜率： 

k = △y / △x

△x = x1 - x0，△y = y1 - y0， (x0, y0)和(x1, y1)是线段的两个端点坐标。然后从线的起点开始，确定最近逼近于直线的y坐标。假设端点坐标都为整数，让x从起点开始到终点，步增为1，计算对应的y坐标，y = kx + B，并取像素(x, round(y))。用这种方法可行、直观，但是效率很差，因为 每步运算都需要一个浮点乘法和一个舍入运算。

yi+1 = kxi+1 + B

= k(xi + △x) + B

= kxi + B + k△x

= yi + k△x

因此，当△x = 1时，有yi+1 = yi + k，每当x步增1，y递增k。

DDA算法程序为：

int round(float a) { return int(a + 0.5); }

void DDAline(int x0, int y0, int x1, int y1, int color)
{
	int x;
	float dx, dy, k, y;
	dx = x1 - x0;
	dy = y1 - y0;
	k = dx / dy;
	y = y0;
	for (x = x0; x <= x1; ++x)
	{
		DrawPixel(x, round(y), color);	
		y = y + k;
	}
}

在这个算法中，y和k必须用浮点数表示，每一步运算又需要将y进行舍入取整，这使得该算法不利于硬件的实现。

中点画线法

中点画线法的基本原理是：

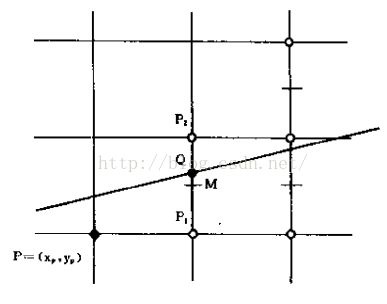
直线在x方向增加一个单位，则在y方向上的增量只能是0和1之间。如图，假设x坐标为xp的的各像素点中，与直线最近者已确定，为(xp, yp)，用实心小圆表示；那么下一个与直线最近的像素只能是正右方P1(xp + 1, yp) 或者是右上方的点P2(xp + 1, yp + 1)两者之一。 M(xp + 1, yp + 0.5) 表示P1和P2的中点，Q是理想直线与垂直线x = xp + 1的交点，如果M点在Q点下方，很明显P2离直线更新一些，如果M在Q的上方，则P1离直线更新一些，我们取离直线最近的那个像素点，如果M和Q重合，我们约定取正右方的那个点。

假设起点和终点为 (x0, y0)和(x1, y1)，则直线方程为：

F(x, y) = ax + by + c， 其中a = y0 - y1， b = x1 - x0，c = x0y1 - x1y0

对于直线上的点，F(x, y) = 0；直线上方的点，F(x, y) > 0；直线下方的点，F(x, y) < 0.  因此，判断M在Q的上方还是下方，只需将M点带入方程计算判别式：

d = F(M) = F(xp + 1, yp + 0.5) = a(xp + 1) + b(yp + 0.5) + c

对于每一个像素的判别式d，根据它的符号来判断下一个像素点。 由于d是xp和yp的线性函数，可采用增量计算来提高运算效率。

在d >= 0的情况下，取正右方像素p1，欲判断再下一个像素应取哪个，应计算：

d1 = F(xp +1 + 1, yp + 0.5) = a(xp + 1 + 1) + b(yp + 0.5) + c  = d + a

注：下一个点的坐标是(xp + 1, yp)，所以再下一个中点就是(xp + 1 +1, yp + 0.5)

故d的增量为a；

在d < 0 ，则取右上方的像素p2，要判断再下一个像素，则应该计算：

d2 = F(xp +1 + 1, yp + 1 + 0.5) = a(xp + 1 + 1) + b(yp + 1 + 0.5) + c  = d + a + b

注：下一个点的坐标是(xp + 1, yp + 1)，所以再下一个中点就是(xp + 1 +1, yp + 1 + 0.5)

d的增量为 a + b.

d的初始值，第一个像素应取左端点(x0, y0)，相应的判别式为：

d0 = F(x0 + 1, y0 + 0.5) = a(x0 + 1) + b(yp + 0.5) + c

=  ax0 + by0 + c + a + 0.5b

= F(x0, y0) + a + 0.5b

由于(x0, y0)在直线上，所以F(x0, y0) = 0，因此，d的初始值为a + 0.5b。

d的初始值包含小数 ，因此 可以用2d来代替d，写出仅包含整数运算的算法：

void MidPointLine(int x0, int y0, int x1, int y1, int color)
{
	int a, b, delta1, delta2, d, x, y;
	a = y0 - y1;
	b = x1 - x0;
	d = 2 * a + b;
	delta1 = 2 * a;
	delta2 = 2 * (a + b);
	x = x0;
	y = y0;
	DrawPixel(x, y, color);
	while (x < x1)
	{
		if (d < 0)
		{
			++x;
			++y;
			d += delta2;
		}
		else
		{
			++x;
			d += delta1;
		}
		DrawPixel(x, y, color);
	}
}

Bresenham画线算法

该算法检查一个误差项的符号就可以确定该列的像素。

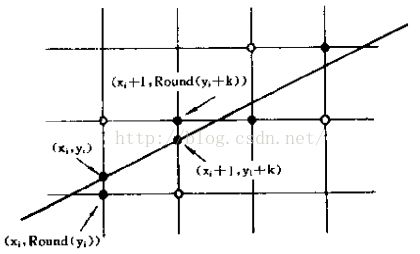
如图，假设x列的像素已确定，其行下标为y，那么下一个像素的列坐标比为x + 1，而行坐标要么不变，要么递增1，是否递增1取决于误差项d的值(如上图所示)。因为直线起始点在像素中心，所以误差项d的初始值为0，x下标每增加1，d的值相应递增直线的斜率值，即d = d + k.  一旦d >= 1，将它的值减去1，使得d的值总保持在0到1之间。当d >= 0.5时，直线与x + 1列垂直网格线交点最接近于当前像素的右上方像素点(x + 1， y + 1)，d < 0.5时则为正右方像素(x + 1, y)。

令 e = d - 0.5，当e >= 0时 ， 下一个像素值y递增1，e < 0时y不递增，e初始值为-0.5. 算法如下：

void Bresenham(int x0, int y0, int x1, int y1, int color)
{
	int x, y, dx, dy;
	float k, e;
	dx = x1 - x0;
	dy = y1 - y0;
	k = dx / dy;
	e = -0.5; // 因为d的初始值为0
	x = x0;
	y = y0;
	for (int i = 0; i <= dx; ++i)
	{
		DrawPixel(x, y, color);
		x += 1;
		e = e + k;
		if (e >= 0) // 伪代码，实际比较浮点数不这样进行比较
		{
			y += 1;
			e = e - 1;
		}
	}
}

写完会发现，该算法会用到小数和除法，为了利于硬件实现，可以改用整数以避免除法，算法中只用到误差项的符号，因此可以作如下替换：

e' = 2 * e * dx;

整数Bresenham算法为：

void Bresenham(int x0, int y0, int x1, int y1, int color)
{
	int x, y, dx, dy;
	float k, e;
	dx = x1 - x0;
	dy = y1 - y0;
	e = -dx
	x = x0;
	y = y0;
	for (int i = 0; i <= dx; ++i)
	{
		DrawPixel(x, y, color);
		x += 1;
		e = e + 2 * dy;
		if (e >= 0) // 伪代码，实际比较浮点数不这样进行比较
		{
			y += 1;
			e = e - 2 * dx;
		}
	}
}

以上所有程序均是考虑斜率在0~1之间的时候~ 

初学者，欢迎各位大牛指出错误！