MoussaTintin

【Learning Notes】生成式对抗网络（Generative Adversarial Networks，GAN）

在学习 V a r i a t i o n a l A u t o - E n c o d e r 时，同时注意到了 G A N 研究的火热。但当时觉得 G A N 非常不成熟（训练不稳定，依赖各种说不清的 t r i c k s ；没有有效的监控指标，需要大量的人工判断，因此难以扩展到图像之外的高维数据）。在读了 G o o d f e l l o w 的 t u t o r i a l 后 [ 2 ] ，开始黑转路人，觉得 G A N 虽然缺点不少，但优点也很明显。 W G A N [ 5 , 6 ] 等工作出现后，开始逐渐路人转粉，对 G A N 产生了兴趣。

这里，我们仅仅从直观上讨论 G A N 框架及相关变种，将理论留待将来讨论。

1. Basic GAN

本质上， G A N 是一种训练模式，而非一种待定的网络结构 [ 1 ] 。

图 1 . G A N 基本框架【 s r c 】

G A N 的基本思想是，生成器和判别器玩一场 “ 道高一尺，魔高一丈 ” 的游戏：判别器要练就 “ 火眼金睛 ” ，尽量区分出真实的样本（如真实的图片）和由生成器生成的假样本；生成器要学着 “ 以假乱真 ” ，生成出使判别器判别为真实的 “ 假样本 ” 。

竞争的理想怦是双方都不断进步 — — （理想情况下）判别器的眼睛越发 “ 雪亮 ” ，生成器的欺骗能力也不断提高。 对抗的胜负无关紧要，重要的是，最后生成器的欺骗能力足够好，能够生成与真实样本足够相似的样本 — — 直观而言，生成的样本看起来像是训练集（如图片）的样本；形式化的，生成器生成样本的分布，应该与训练集样本分布接近。

理论上可以，在理想条件下，生成器是可以通过这种对抗得到目标分布的（即生成足够真实的样本）。

假设要训练数据为灰度 M N I S T （归一化为 [ 0 , 1 ] 之间），生成器（ g e n e r a t o r ）可以为任意输入为隐变量维度，输出为 1 x 2 8 x 2 8 的模型。一个示例模型定义如下：

def build_generator(latent_size):
    model = Sequential()
    model.add(Dense(1024, input_dim=latent_size, activation='relu'))
    model.add(Dense(28 * 28, activation='tanh'))
    model.add(Reshape((1, 28, 28)))
    return model

判别器（ d i s c r i m i n a t o r ）可以为任意输入 1 x 2 8 x 2 8 ，输出为 1 维且在 [ 0 , 1 ] 之间（经过 s i g m o i d 激活）的模型。一个示例模型定义如下：

def build_discriminator():
    model = Sequential()
    model.add(Flatten(input_shape=(1, 28, 28)))
    model.add(Dense(256, activation='relu'))
    model.add(Dense(128, activation='relu'))
    model.add(Dense(1)， activation='sigmoid')   
    return model

输出值表示判别器判别输入样本为真的概率。即输出值越接近 1 ，判别器越确信样本为真；输出值越接近 0 ，判别器越确信样本为假。

判别器

L D = - Σ i log (D (x i)) - Σ i log (1 - D (G (z i)))

判别器的训练的目标为：对于真实样本，输出尽量接近 1 ；对于生成器生成的假样本，输出尽量接近 0 。
也即训练判别器时，真实样本的标签为 1 ，生成样本的标签为 0 。

生成器

L G = Σ i log (1 - D (G (z i)))

判别器的训练的目标为生成的假样本，使判别器的输出尽量接近 1 ，即尽量以假乱真。
为了解决训练过程中，梯度消失的问题，一般使用如下损失函数 ( T r i c k 2 ) ：

L G = - Σ i log (D (G (z i)))

为使用这个损失函数，只需要将生成样本的标签为 1 ，同时使用变通的交叉熵损失函数。

G A N 的训练流程如下 [ 1 ] ：

\nabla θ 1 m Σ m i = 1 - log (D (G (z (i))))

G A N 足够简单，也有理论上的保证。但在实践中，需要许多技巧和运气才能正常把 “ 游戏玩下去 ” 。这里，我们不考虑理论，而是关注不要 G A N 变种在损失函数设计的差异。

2. Least Squares GAN

我们以 [ 4 ] 中 E q ( 9 ) 为例来介绍 L S G A N 。其中判别器的定义如下：

def build_discriminator():
    model = Sequential()
    model.add(Flatten(input_shape=(1, 28, 28)))
    model.add(Dense(256, activation='relu'))
    model.add(Dense(128, activation='relu'))
    model.add(Dense(1)， activation='linear') ## change 1    
    return model

与 b a s i c G A N 唯一不同在判别器的最后输出不使用 s i g m o i d 激活，而是使用了线性函数（也即不使用激活）（第 6 行 c h a n g e 1 ）。

有了生成器和判别器的定义，我们来实际构造两者以用于训练：

# 构造判别器
disc = build_discriminator()
disc.compile(optimizer=Adam(lr=lr),loss='mse')

# 构建生成器
generator = build_generator(latent_size)
latent = Input(shape=(latent_size,))
# 生成假图片
fake = generator(latent)
# 我们要训练生成器，因此固定判别的权值不变
disc.trainable = False
fake = disc(fake)
combined = Model(input=latent, output=fake)
combined.compile(optimizer=Adam(lr=lr), loss='mse')

不同于 b a s i c G A N , L S G A N 的训练损失函数由交叉熵改为 M S E ( M e a n S q u a r e d E r r o r ) 。

for epoch in range(nb_epochs):
    for index in range(nb_batches):
        ## 1) 训练判别器 
        # 1.1采样隐变量并生成假样本
        noise = np.random.uniform(-1, 1, (batch_size, latent_size))
        generated_images = generator.predict(noise, verbose=0)
        # 1.2 从训练中采样真实样本
        image_batch = X_train[index * batch_size:(index + 1) * batch_size]
        label_batch = y_train[index * batch_size:(index + 1) * batch_size]        
        # 利用真假数据进行训练
        X = np.concatenate((image_batch, generated_images))
        # 设定真假数据的损失，a == 0, b == 1
        y = np.array([1] * len(image_batch) + [0] * batch_size)
        disc.train_on_batch(X, y)

        ## 2）训练生成器
        # 采样隐变量       
        noise = np.random.uniform(-1, 1, (batch_size, latent_size))
        target = np.ones(batch_size) # 设定生成样本的损失 c == b == 1
        combined.train_on_batch(noise, target)

图 2 是训练过程中，由生成器采样的几张示例图片。完整的示例可以参见 r e p o 。

图 2 . L S G A N 随机采样生成的图片（ E p o c h : 4 4 3 ）

由于仅作为示例以及时间和计算资源的限制，从模型结构到优化器的参数都没有经过任何调优。因此，这里生成的图片的质量不应该做为算法优劣的依据（下同）。

3. Wasserstein GAN(WGAN)

W G A N 采用线性的损失函数，为此我们定义：

 def dummy_loss(loss_to_backprop, y_pred):
    return K.mean(loss_to_backprop * y_pred) # delta == loss_to_backprop

disc.compile(optimizer=Adam(lr=lr),loss=dummy_loss)
combined.compile(optimizer=Adam(lr=lr), loss=dummy_loss)

为应用这个损失函数，代码更改如下（第 1 2 和 1 8 行， c h a n g e 2 、 3 ）。

for epoch in range(nb_epochs):
    for index in range(nb_batches):
        ## 1) 训练判别器 
        # 1.1采样隐变量并生成假样本
        noise = np.random.uniform(-1, 1, (batch_size, latent_size))
        generated_images = generator.predict(noise, verbose=0)
        # 1.2 从训练中采样真实样本
        image_batch = X_train[index * batch_size:(index + 1) * batch_size]
        label_batch = y_train[index * batch_size:(index + 1) * batch_size]        
        # 利用真假数据进行训练
        X = np.concatenate((image_batch, generated_images))        
        y = np.array([-1] * len(image_batch) + [1] * batch_size) ## change 2
        disc.train_on_batch(X, y)

        ## 2）训练生成器
        # 采样隐变量       
        noise = np.random.uniform(-1, 1, (batch_size, latent_size))
        target = -np.ones(batch_size) ## change 3
        combined.train_on_batch(noise, target)

W G A N 有如下突出优点 [ 6 ] ：
* 训练稳定，不需要平稳生成器和判别器。
* l o s s 值与生成样本质量相关，可以用来监督训练进程，不需要人工判断干预。

完整的示例可以参见 r e p o 。读者可以自行验证， D _ l o s s 及生成图像的质量变化。

4. GLSGAN

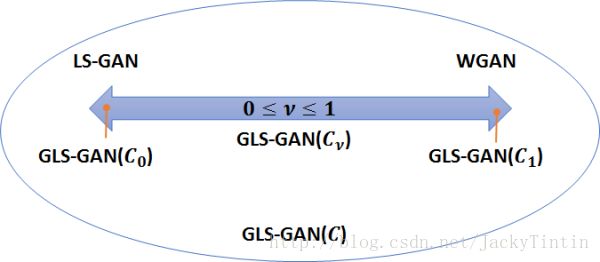
[ 7 ] 提出了 L o s s S e n s i t i v e G A N ，并随后发现，可以和 W G A N 在统一的框架下研究，即 g e n e r a l i z e d L S G A N （图 3 ）。

图 3 . 【 s r c 】

G L S G A N 使用 L e a k y R e L U 作用激活，其中 s∈（−∞,1] 。

L e a k y R e L U (x) = {x, i f x \geq 0, s \cdot x, x < 0.

def build_discriminator():
    model = Sequential()
    model.add(Flatten(input_shape=(1, 28, 28)))
    model.add(Dense(256, activation='relu'))
    model.add(Dense(128, activation='relu'))
    model.add(Dense(1)， activation='linear')
    model.add(LeakyReLU(slope)) ##
    return model

下面是不同 s 下，训练的模型生成的示例图片。

图 4 . S l o p e : 1 ( W G A N ) , E p o c h : 1 7 0

图 5 . S l o p e : 0 ( L o s s S e n s i t i v e G A N ) , E p o c h : 1 8 9

图 6 . S l o p e : - 1 ( L 1 L o s s ) , E p o c h : 3 9 9

非线性损失

G L S G A N 并不限定损失函数为（分段）线性。这里使用 E x p o n e n t i a l L i n e a r U n i t （ E L U ）。

E L U (x) = {x, i f x \geq 0, α \cdot (exp (x) - 1), x < 0.

【Learning Notes】生成式对抗网络（Generative Adversarial Networks，GAN）_第8张图片

图 7 . E x p o n e n t i a l L i n e a r U n i t v s . R e L U 【 s r c 】

def build_discriminator():
    # Other Code goes here...
    model.add(ELU)  # Exponential Linear Unit
    return model

图 8 . E L U , E p o c h : 3 6 7

一个完整的示例见 r e p o 。基于 t o r c h 的 o f f i c i a l r e p o 。

5. 讨论

损失函数

损失函数唯一重要的地方在于，不断驱动两个网络的竞争。直观上，判别网络将真实样本和生成样本，向坐标轴上的两个不同的区域移动。
* 对于 b a s i c G A N ，这两个区域分别分别是 0 （生成）和 1 （真实），使用的损失函数是对数函数（ f(x)=−log(x) ）（即交叉熵） [ 1 ] 。
* 对于 L e a s t S q u a r e d G A N ，这两个区域分别是 a 和 b （ a < b ），使用的损失函数是二次函数（ f(x)=x2 ） [ 4 ] 。
* 对于 W G A N ，这两个区域分别 +∞ （真实样本）和 −∞ （生成样本），使用的是线性损失函数（ f(x)=x ） [ 6 ] 。
* 对于 L o s s - S e n s i t i v e G A N ，这两个区域分别是 +∞ （真实样本）和 (−∞,0] [ 7 ] ，使用的是 R e L u 损失函数。
* 对于 G e n e r a l i z e d L S G A N （ 0<γ<1 ），这两个区域分别是 +∞ （真实样本）和 (−∞,0] [ 7 ] ，使用的是 L e a k y R e L u 损失函数。
* 对于 G e n e r a l i z e d L S G A N （ γ<0 ），这两个区域分别是 +∞ （真实样本）和 0 [ 7 ] ，使用的是分段线性的损失函数。

从损失函数的角度， B a s i c G A N 几乎选择了一个最差的方案 — — 经过 s i g m o i d 激活后，损失函数在 0 - 1 两端都存在饱和区。

关于GLSGAN

当 γ<0 时，从形式上， G L S G A N 其实已经不能叫做 L o s s S e n s i t i v e 了。因为此时 G L S G A N 的行为更向是 L e a s t S q u a r e s G A N — — 将生成样本向某个点推（零点）。不过 G L S G A N 对于真实样本更激进，它会不断将真实样本向 +∞ 推。另一个不同是， G L S G A N 使用线性的函数，而 L S G A N 使用二次函数。

T O D O 此处有一个疑问待解决：文章中说 L e a s t S q u a r e s G A N 也存在梯度消失的问题。从形式上看，虽然一次函数在极值附近梯度接近 0 ，但由于正负样本的损失函数的极值点不同，因此，直觉上，在对抗训练过程中应该不会出现梯度消失的现象。看到需要进一步提高理论修养。

Regularities

这里我们没有关注正则性约束，但 W G A N ， G L S G A N 要求判别器是 L i p s c h i t z （相对于模型参数）。直观上， L i p s c h i t z 保证训练过程中，不会因为参数更新引起模型的跳跃性变化，确保训练过程平稳。

6. 结语

形式上，各种方法仅仅是损失函数不太一样，但损失函数的选择并不 t r i v i a l 。 b a s i c G A N 训练困难已经表明了 G A N 对抗的训练方式对损失函数的非常的敏感。没有严谨的理论支撑，随意的损失函数并不能保证训练如预期进行（收敛且稳定）。
鲁棒的 G A N 训练方法对于 G A N 在广阔领域的应用将是非常大的推动力（如最近的压缩感知应用）。
对不同损失函数（不同 G A N ）的性质，目前还缺少系统性的比较研究，期待更新的研究结果。

References

I a n G o o d f e l l o w e t a l . ( 2 0 1 4 ) . G e n e r a t i v e A d v e r s a r i a l N e t w o r k s .
I a n G o o d f e l l o w . ( 2 0 1 6 ) . N I P S 2 0 1 6 T u t o r i a l : G e n e r a t i v e A d v e r s a r i a l N e t w o r k s .
N o w o z i n e t a l . ( 2 0 1 6 ) . f - G A N : T r a i n i n g G e n e r a t i v e N e u r a l S a m p l e r s u s i n g V a r i a t i o n a l D i v e r g e n c e M i n i m i z a t i o n .
M a o e t a l . ( 2 0 1 6 ) . L e a s t S q u a r e s G e n e r a t i v e A d v e r s a r i a l N e t w o r k s .
A r j o v s k y e t a l . ( 2 0 1 6 ) . T o w a r d s P r i n c i p l e d M e t h o d s f o r T r a i n i n g G e n e r a t i v e A d v e r s a r i a l N e t w o r k s .
A r j o v s k y e t a l . ( 2 0 1 7 ) . W a s s e r s t e i n G A N .
Q i . ( 2 0 1 7 ) . L o s s - S e n s i t i v e G e n e r a t i v e A d v e r s a r i a l N e t w o r k s o n L i p s c h i t z D e n s i t i e s .
A n I n c o m p l e t e M a p o f t h e G A N m o d e l s .
L S - G A N ：把 G A N 建立在 L i p s c h i t z 密度上 .
广义 L S - G A N （ G L S - G A N ) .