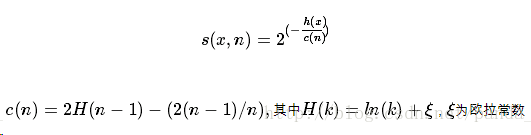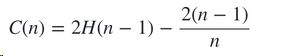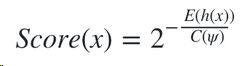异常点检测系列之IsolationForest 算法及其实现
"An outlier is an observation which deviates so much from other observations as to arouse suspicions that it was generated by a different mechanism."
异常检测 (anomaly detection),或者又被称为“离群点检测” (outlier detection),是机器学习研究领域中跟现实紧密联系、有广泛应用需求的一类问题。但是,什么是异常,并没有标准答案,通常因具体应用场景而异。
通常我们定义“异常”的两个标准或者说假设:
异常数据跟样本中大多数数据不太一样。
异常数据在整体数据样本中占比比较小。对于异常检测而言,最直接的做法是利用各种统计的、距离的、密度的量化指标去描述数据样本跟其他样本的疏离程度(详见异常检测概论)。而 Isolation Forest (Liu et al. 2011) 的想法要巧妙一些,它尝试直接去刻画数据的“疏离”(isolation)程度,而不借助其他量化指标。Isolation Forest 因为简单、高效,在学术界和工业界都有着不错的名声。
Isolation Forest 简称 IForest,这个算法是周志华老师在2010年提出的一个异常值检测算法,在工业界很实用,算法效果好,时间效率高,能有效处理高维数据和海量数据,也是本文主要介绍的一种算法。
算法起源于08年的一篇论文《Isolation Forest》,这论文由澳大利亚莫纳什大学的两位教授Fei Tony Liu, Kai Ming Ting和南京大学的周志华教授共同完成,而这三人在2011年又发表了《Isolation-based Anomaly Detection》,这两篇论文算是确定了这个算法的基础。
论文地址:
http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf
http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/tkdd11.pdf
iForest (Isolation Forest)孤立森林 是一个基于Ensemble的快速异常检测方法,具有线性时间复杂度和高精准度。IF采用二叉树去对数据进行切分,数据点在二叉树中所处的深度反应了该条数据的“疏离”程度。整个算法大致可以分为两步:iForest属于Non-parametric和unsupervised的方法,即不用定义数学模型也不需要有标记的训练。怎么来切这个数据空间是iForest的设计核心思想,本文仅介绍最基本的方法。由于切割是随机的,所以需要用ensemble的方法来得到一个收敛值(蒙特卡洛方法),即反复从头开始切,然后平均每次切的结果。iForest 由t个iTree(Isolation Tree)孤立树 组成,每个iTree是一个二叉树结构,其算法流程:
1.构建N棵iTree,为每棵树随机做无放回采样生成训练集。iTree是一棵随机二叉树,给定数据集DataSet,假设数据集内所有属性都是连续型变量,iTree构造过程可以描述为:
首先随机选择数据的一个属性A,然后随机选择属性A中的一个值V,按照属性A的值对每条数据进行树的分裂,将小于V的记录放在左孩子上,把大于V的记录放在右孩子上,然后按上述过程递归构建树,直到满足如下条件:
1.传入的数据集只有一条记录或者多条一样的记录;
2.树的高度达到了限定高度
2.进行预测:预测的过程就是把测试数据在iTree树上沿对应的分支往下走,走到达到叶子节点,并记录着过程中经过的路径长度h(x)。将h(x)带入到异常值评分函数中,得到异常值分数,公式如下图所示:
s(x,n)就是记录x在由n个样本的训练数据构成的iTree的异常指数,s(x,n)取值范围为[0,1],越接近1表示是异常点的可能性高,越接近0表示是正常点的可能性比较高,如果大部分的训练样本的s(x,n)都接近于0.5,说明整个数据集都没有明显的异常值。
第二种解释:
训练:构建一棵 iTree 时,先从全量数据中抽取一批样本,然后随机选择一个特征作为起始节点,并在该特征的最大值和最小值之间随机选择一个值,将样本中小于该取值的数据划到左分支,大于等于该取值的划到右分支。然后,在左右两个分支数据中,重复上述步骤,直到满足如下条件:
数据不可再分,即:只包含一条数据,或者全部数据相同。
二叉树达到限定的最大深度。
预测:
计算数据 x 的异常分值时,先要估算它在每棵 iTree 中的路径长度(也可以叫深度)。具体的,先沿着一棵 iTree,从根节点开始按不同特征的取值从上往下,直到到达某叶子节点。假设 iTree 的训练样本中同样落在 x 所在叶子节点的样本数为 T.size ,则数据 x 在这棵 iTree 上的路径长度 h(x) ,可以用下面这个公式计算:
公式中,e 表示数据 x 从 iTree 的根节点到叶节点过程中经过的边的数目,C(T.size) 可以认为是一个修正值,它表示在一棵用 T.size 条样本数据构建的二叉树的平均路径长度。一般的,C(n) 的计算公式如下:
其中,H(n-1) 可用 ln(n-1)+0.5772156649 估算,这里的常数是欧拉常数。数据 x 最终的异常分值 Score(x) 综合了多棵 iTree 的结果:
公式中,E(h(x)) 表示数据 x 在多棵 iTree 的路径长度的均值,$\psi$ 表示单棵 iTree 的训练样本的样本数,$C(\psi)$ 表示用 $\psi$ 条数据构建的二叉树的平均路径长度,它在这里主要用来做归一化。
从异常分值的公式看,如果数据 x 在多棵 iTree 中的平均路径长度越短,得分越接近 1,表明数据 x 越异常;如果数据 x 在多棵 iTree 中的平均路径长度越长,得分越接近 0,表示数据 x 越正常;如果数据 x 在多棵 iTree 中的平均路径长度接近整体均值,则打分会在 0.5 附近。
个人理解:
相比较与基于密度和基于距离的异常值检测算法,iForest 采用空间划分的策略来查找异常值,在这个算法中,异常值存在于树种较浅层的位置,可以理解为,假设我们用一个随机超平面来切割(split)数据空间(data space), 切一次可以生成两个子空间(想象拿刀切蛋糕一分为二)。之后我们再继续用一个随机超平面来切割每个子空间,循环下去,直到每子空间里面只有一个数据点为止。直观上来讲,我们可以发现那些密度很高的簇是可以被切很多次才会停止切割,但是那些密度很低的点很容易很早的就停到一个子空间了。(这个例子引用自http://www.jianshu.com/p/5af3c66e0410)
对于这个算法,我个人理解为这是一种kd树和随机森林模型的思想融合的产物,其利用类似kd树对空间检索和划分的理论,找到那些游离于整体的异常值的点,然后通过对树的集成思想,增强整个模型的泛化能力和对异常值鉴别的准确度,基于以上特性,iForest具有线性时间复杂度和对海量数据的处理能力,并且随着树的数量越多,算法越稳定。
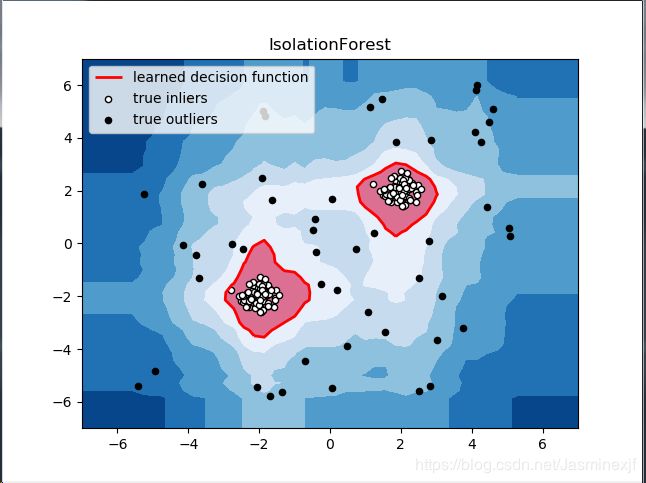
sklearn示例
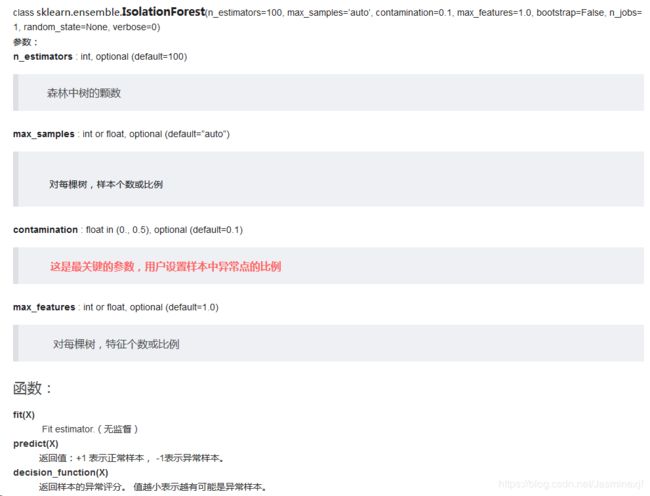
iForest 已经被集成在scikit-learn的0.19版本中,在Sk-learn中其评分函数越低,表示数据是越正常,越高则为异常值的可能性越大。
http://scikit-learn.org/dev/modules/generated/sklearn.ensemble.IsolationForest.html1. iForest具有线性时间复杂度。因为是ensemble的方法,所以可以用在含有海量数据的数据集上面。通常树的数量越多,算法越稳定。由于每棵树都是互相独立生成的,因此可以部署在大规模分布式系统上来加速运算。
2. iForest不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度,建完树后仍然有大量的维度信息没有被使用,导致算法可靠性降低。高维空间还可能存在大量噪音维度或无关维度(irrelevant attributes),影响树的构建。对这类数据,建议使用子空间异常检测(Subspace Anomaly Detection)技术。此外,切割平面默认是axis-parallel的,也可以随机生成各种角度的切割平面,详见“On Detecting Clustered Anomalies Using SCiForest”。
3. iForest仅对Global Anomaly 敏感,即全局稀疏点敏感,不擅长处理局部的相对稀疏点 (Local Anomaly)。目前已有改进方法发表于PAKDD,详见“Improving iForest with Relative Mass”。
4. iForest推动了重心估计(Mass Estimation)理论发展,目前在分类聚类和异常检测中都取得显著效果,发表于各大顶级数据挖掘会议和期刊(如SIGKDD,ICDM,ECML)。
Isolation Forest 是无监督的异常检测算法,在实际应用时,并不需要黑白标签。需要注意的是:(1)如果训练样本中异常样本的比例比较高,违背了先前提到的异常检测的基本假设,可能最终的效果会受影响;(2)异常检测跟具体的应用场景紧密相关,算法检测出的“异常”不一定是我们实际想要的。比如,在识别虚假交易时,异常的交易未必就是虚假的交易。所以,在特征选择时,可能需要过滤不太相关的特征,以免识别出一些不太相关的“异常”。
#!/usr/bin/python
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
from scipy import stats
rng = np.random.RandomState(42)
# 构造训练样本
n_samples = 200 #样本总数
outliers_fraction = 0.25 #异常样本比例
n_inliers = int((1. - outliers_fraction) * n_samples)
n_outliers = int(outliers_fraction * n_samples)
X = 0.3 * rng.randn(n_inliers // 2, 2)
X_train = np.r_[X + 2, X - 2] #正常样本
X_train = np.r_[X_train, np.random.uniform(low=-6, high=6, size=(n_outliers, 2))] #正常样本加上异常样本
# fit the model
clf = IsolationForest(max_samples=n_samples, random_state=rng, contamination=outliers_fraction)
clf.fit(X_train)
# y_pred_train = clf.predict(X_train)
scores_pred = clf.decision_function(X_train)
threshold = stats.scoreatpercentile(scores_pred, 100 * outliers_fraction) #根据训练样本中异常样本比例,得到阈值,用于绘图
# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-7, 7, 50), np.linspace(-7, 7, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("IsolationForest")
# plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7), cmap=plt.cm.Blues_r) #绘制异常点区域,值从最小的到阈值的那部分
a = plt.contour(xx, yy, Z, levels=[threshold], linewidths=2, colors='red') #绘制异常点区域和正常点区域的边界
plt.contourf(xx, yy, Z, levels=[threshold, Z.max()], colors='palevioletred') #绘制正常点区域,值从阈值到最大的那部分
b = plt.scatter(X_train[:-n_outliers, 0], X_train[:-n_outliers, 1], c='white',
s=20, edgecolor='k')
c = plt.scatter(X_train[-n_outliers:, 0], X_train[-n_outliers:, 1], c='black',
s=20, edgecolor='k')
plt.axis('tight')
plt.xlim((-7, 7))
plt.ylim((-7, 7))
plt.legend([a.collections[0], b, c],
['learned decision function', 'true inliers', 'true outliers'],
loc="upper left")
plt.show()