5、【李宏毅机器学习（2017）】Logistic Regression（Logistic回归）

本篇博客将在分类模型基础上继续，并开始学习一种常用的分类算法——Logistic回归，同样按照机器学习简介中机器学习建模步骤。

---

目录

---

step1

同样考虑一个而分类问题，此时Function Set 为 fx=Pw,b(C1|x)=σ(z)=11+exp{−(wx+b)} f x = P w , b ( C 1 | x ) = σ ( z ) = 1 1 + e x p { − ( w x + b ) } ，如果 Pw,b(C1|x)>0.5 P w , b ( C 1 | x ) > 0.5 ，class为 C1 C 1 ，否则为 C2 C 2 。

step2

class C1 C 1 的标记 ŷ  y ^ 为1，class C2 C 2 的标记 ŷ  y ^ 为0， Pw,b(C1|x)=fw,b(x)ŷ +(1−fw,b(x))1−ŷ  P w , b ( C 1 | x ) = f w , b ( x ) y ^ + ( 1 − f w , b ( x ) ) 1 − y ^ ，

L(w,b)=∏i=1nP(C1|xi),lnL=∑i=1n[ŷ ifw,b(xi)+(1−ŷ i)(1−fw,b(xi))] L ( w , b ) = ∏ i = 1 n P ( C 1 | x i ) , l n L = ∑ i = 1 n [ y ^ i f w , b ( x i ) + ( 1 − y ^ i ) ( 1 − f w , b ( x i ) ) ]

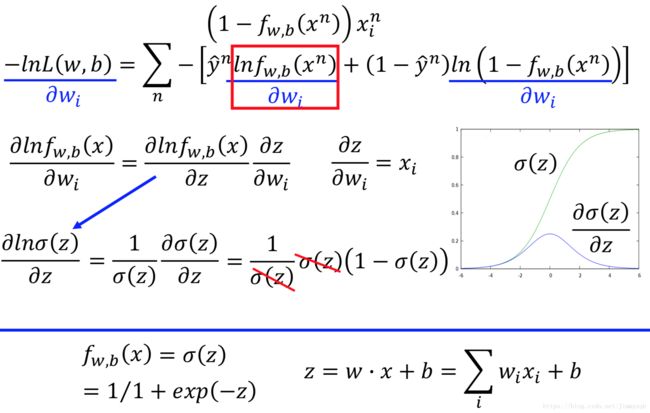
根据极大似然估计，为了极大化 L(w,b) L ( w , b ) ，等价于极小化 −lnL − l n L ，求解得到 w∗,b∗=argminw,b∑ni=1−[ŷ ifw,b(xi)+(1−ŷ i)(1−fw,b(xi))] w ∗ , b ∗ = a r g m i n w , b ∑ i = 1 n − [ y ^ i f w , b ( x i ) + ( 1 − y ^ i ) ( 1 − f w , b ( x i ) ) ]

C(f(xn),(̂ y)n)=−[ŷ nfw,b(xn)+(1−ŷ n)(1−fw,b(xn))] C ( f ( x n ) , ( ^ y ) n ) = − [ y ^ n f w , b ( x n ) + ( 1 − y ^ n ) ( 1 − f w , b ( x n ) ) ] 表示Cross entropy between two Bernoulli distribution。

step3

Logistic Regression与Linear Regression

差异

为什么在Logistic回归中使用Cross entropy而非MSE做模型选择的标准？

假设Logistic回归使用和线性回归中一样的MSE做选择标准，

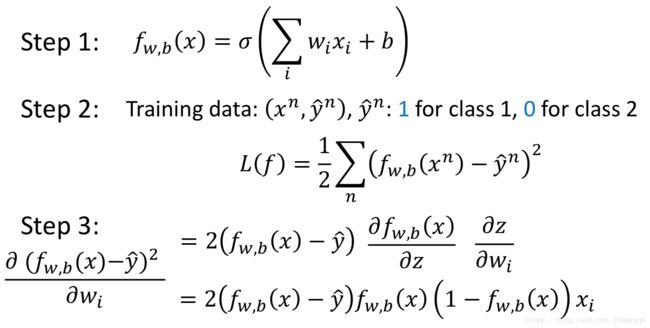
• 假设 ŷ =1,fw,b(xn)=1 y ^ = 1 , f w , b ( x n ) = 1 ，此时接近目标，带入计算得到 ∂L∂wi=0 ∂ L ∂ w i = 0 ，没有问题
• 假设 ŷ =1,fw,b(xn)=0 y ^ = 1 , f w , b ( x n ) = 0 ，此时距离目标很远，带入计算得到 ∂L∂wi=0 ∂ L ∂ w i = 0 ，结果错误
• 假设 ŷ =0,fw,b(xn)=1 y ^ = 0 , f w , b ( x n ) = 1 ，此时距离目标很远，带入计算得到 ∂L∂wi=0 ∂ L ∂ w i = 0 ，结果错误
• 假设 ŷ =0,fw,b(xn)=0 y ^ = 0 , f w , b ( x n ) = 0 ，此时接近目标，带入计算得到 ∂L∂wi=0 ∂ L ∂ w i = 0 ，没有问题

如图，横轴坐标表示参数的值，纵坐标为总损失，比较使用Cross Entropy（黑色）和Square Error（红色）标准的不同：

Cross Entropy曲面陡峭，因此当初始值距离目标值越远微分值越大，参数更新越快；Square Error的曲面和平坦，当初始值距离目标值远时微分值也不大，参数更新慢，一开始就卡住，即使考虑在微分值很小把学习速率设置大也不可行，因为当趋近于目标值的时候微分值也很小，过大的学习速率会导致跨过目标值的点。

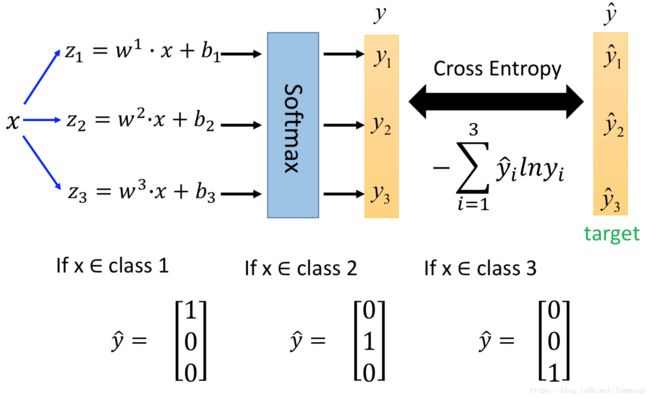
Multi-class Classification

现在考虑多分类问题，例如有类别 C1,C2,C3 C 1 , C 2 , C 3 的数据，推导的思路和Logistic回归一样，Logistic回归等价于softmax回归只有两类的情况，

Discriminative v.s. Generative

对于Discriminative模型，我们没有做任何的假设，只是通过训练训练集合找到 w,b w , b ，对于Generative模型我们往往对数据的分布做出先验的假设，并且估计出每一类别分布的参数。

在一个具体的例子里使用朴素贝叶斯进行估计——

测试样本被判为Class2，这是由于在朴素贝叶斯分类中假设了第一个特征和第二个特征是独立的且样本不平衡原因导致的。

• 通常我们相信Discriminative模型优于Generative模型
• Generative模型的优点
  – 由于做出假设，所需的样本量较少
  – 对噪声（比如本身就是标记错了的样本）较为稳健
  – 先验数据可以通过其他渠道得到

Logistic回归的局限性

对于线性不可分的数据没有办法分类，此时考虑在Logistic回归建模之前对特征进行转化，如图，左图中线性不可分的数据在特征转化后可以很好地被红色直线区分开。

这就是神经网络（深度学习）的雏型！！！