算法学习（一）：DBSCAN聚类算法

由于学习需要，最近专门了解了DBSCAN聚类算法，将学习的记录写下来，备用。

一、DBSCAN算法简介

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。
该算法将具有足够密度的区域划分为簇，并在具有“噪声”的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。
对DBSCAN的基本概念的初步认识：
1. 对于簇中的任意一个点，它周围局部点密度必须超过某个阈值；
2. 簇中的点在空间上是相互关联的。

二、DBSCAN算法的5个基本定义

任意点p的局部点密度由两个参数定义，即Eps（邻域的最大半径）及MinPts（在Eps邻域中的最少点数）。相关一些概念的定义如下：
定义1（Eps邻域）　
给定一个对象p，p的Eps邻域NEps（p）定义为以p为核心，以Eps为半径的d维超球体区域，即：

其中，D为d维实空间上的数据集， dist (p,q)表示D中的2个对象p和q之间的距离。

定义2（核心点与边界点）　
对于对象p∈D，给定一个整数MinPts，如果p的Eps邻域内的对象数满足|NEps(p)|≥MinPts ，则称p为(Eps，MinPts ) 条件下的核心点；不是核心点但落在某个核心点的Eps邻域内的对象称为边界点。

定义3（直接密度可达）　
如图所示，给定 (Eps，MinPts ) ，如果对象p和q同时满足如下条件
① p∈ NEps(q) ；
② |NEps(q)|≥MinPts （即q是核心点）。
则称对象p是从对象q出发，直接密度可达的。

定义4（密度可达）　
如图所示，给定数据集D，当存在一个对象链 p1，p2，p3，…，pn， 其中 p1 = q ， pN= p，对于 pi ∈D ，如果在条件(Eps，MinPts ) 下 pi+1从pi 直接密度可达，则称对象p从对象q在条件 (Eps，MinPts )下密度可达。密度可达是非对称的，即p从q密度可达不能推出q也从p密度可达。

定义5（密度相连）　
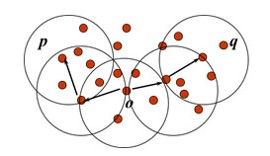
如图所示，如果数据集D中存在一个对象o，使得对象p和q是从o在 (Eps，MinPts )条件下密度可达的，那么称对象p和q在 (Eps，MinPts )条件下密度相连。密度相连是对称的。

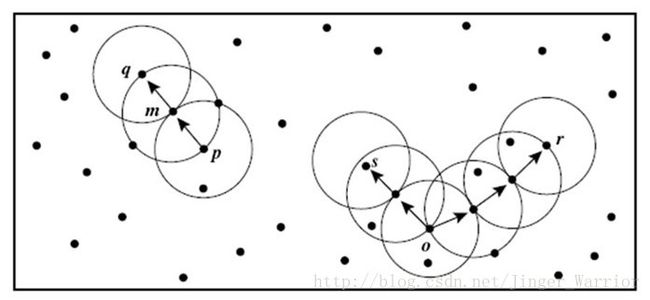
关于密度可达和密度相连，示例如图，给定圆的半径Eps，MinPts=3。
在被标记的点中，m，p，o和r都是核心点，因为它们的Eps邻域内都至少包含3个对象，对象q是从m直接密度可达的。对象m是从p直接密度可达的。对象q是从p（间接）密度可达，但p并不是从q密度可达，因为q不是核心点。
类似地，r和s是从o密度可达的；而o是从r密度可达的。因此，o、r和s都是密度相连的。

三、DBSCAN算法流程

输入：
Eps ——半径
MinPts ——给定点在E邻域内成为核心对象的最小邻域点数。
D ——包含n个对象的数据库。

输出：目标类簇集合

方法：
① 任意选取一个没有加簇标签的点p ；
② 得到所有从p关于Eps和MinPts密度可达的点；
③ 如果p是一个核心点，形成一个新的簇，给簇内所有对象点加簇标签；
④ 如果p是一个边界点，没有从p密度可达的点，DBSCAN将访问数据库中的下一个点；
⑤ 继续这一过程，直到数据库中的所有点都被处理。

四、DBSCAN算法的优缺点

优点：
1） 形成的簇可以具有任意形状和大小；
2） 可以自动确定形成的簇数目；
3） 可以分离簇和环境噪声；
4） 可以被空间索引结构所支持；
5） 效率高，即使对大数据集也是如此；
6） 一次扫描数据即可完成聚类。

缺点：
1） 只能发现密度相仿的簇；
2） 对用户定义的参数（Eps和MinPts）是敏感的，参数难以确定（特别是对于高维数据），设置的细微不同可能导致差别很大的聚类；
3） 所使用参数Eps和MinPts是两个全局参数，不能刻画高维数据内在的聚类结构，因为真实的高维数据常常具有非常倾斜的分布；
4） 计算复杂度至少为 O(n2)，若采用空间索引，计算复杂度为 O(nlogn)。

举个例子

这是聚类以后的结果，得到的图形是不规则的，可以是任意的图形，这个结果不是我运行出来的，找不到这个特殊的数据集。

这个结果看起来很复杂，但是也体现了DBSCAN算法的有点，对于任意聚类形状都有良好的效果，关键在于对领域半径Eps和最小点数minPts的选择。

最后这个结果，才是我运行出来的，没有特殊数据集，所以只能用python中的random（）产生了一个随机数据集，所以得到的结果并不是很有特点。但也能明显的看出噪声点，以及聚类的结果。

用python编写的DBSCAN聚类算法

# -*- coding: utf-8 -*-
"""
Created on Mon May 01 21:22:45 2017

@author: Administrator
"""

from matplotlib.pyplot import *  
from collections import defaultdict  
import random  

 #计算相邻的数据点的距离
def dist(p1, p2):  
    return ((p1[0]-p2[0])**2+ (p1[1]-p2[1])**2)**(0.5)  

 #随机生成约100个坐标点
all_points=[]  

for i in range(100):  
    randCoord = [random.randint(1,50), random.randint(1,50)]  
    if not randCoord in all_points:
        all_points.append(randCoord)  


#取领域的最大半径Eps = 8， 阈值minPts = 8  
E = 8  
minPts = 8 

#找出核心点  
other_points =[]  
core_points=[]  
plotted_points=[]  
for point in all_points:
    point.append(0) # assign initial level 0  
    total = 0  
    for otherPoint in all_points:
        distance = dist(otherPoint,point)  
        if distance<=E:
            total+=1  

    if total > minPts:  
        core_points.append(point)  
        plotted_points.append(point)  
    else:
        other_points.append(point)  

#找出边界点  
border_points=[]  
for core in core_points:  
    for other in other_points:
        if dist(core,other)<=E:
            border_points.append(other)  
            plotted_points.append(other)  


#执行算法  
cluster_label=0  

for point in core_points:
    if point[2]==0:
        cluster_label+=1  
        point[2]=cluster_label  

    for point2 in plotted_points:
        distance = dist(point2,point)  
        if point2[2] ==0 and distance<=E:
            print point, point2  
        point2[2] =point[2]  


#给点加上簇标签 
cluster_list = defaultdict(lambda: [[],[]])  
for point in plotted_points:
    cluster_list[point[2]][0].append(point[0])  
    cluster_list[point[2]][1].append(point[1])  

markers = ['*','+','.','d','^','v','>','<','p']  

#画出簇 
i=0  
print cluster_list  
for value in cluster_list:
    cluster= cluster_list[value]  
    plot(cluster[0], cluster[1],markers[i])  
    i = i%10+1  

#画出噪声点  
noise_points=[]  
for point in all_points:  
    if not point in core_points and not point in border_points:  
        noise_points.append(point)  
noisex=[]  
noisey=[]  
for point in noise_points:  
    noisex.append(point[0])  
    noisey.append(point[1])  
plot(noisex, noisey, "o")  

title(str(len(cluster_list))+" clusters created with E ="+str(E)+" Min Points="+str(minPts)+" total points="+str(len(all_points))+" noise Points = "+ str(len(noise_points)))  
axis((0,60,0,60))  
show()