机器学习——性能评估指标
性能评估指标
- 1. 分类算法的性能评估指标
- 1.1 精确率与召回率
- 1.2 F1-score
- 1.3 AUC与ROC
- 1.3.1 ROC曲线
- 1.3.2 AUC值
- 1.3.3 为什么使用ROC和AUC
- 2. 回归算法的性能评估指标
- 2.1 平均绝对误差(MAE)
- 2.2 平均平方误差(MSE)
- 2.3 均方根误差(RMSE)
- 2.4 决定系数(R2 score)
- 2.5 交叉验证(cross-validation)
机器学习算法主要分为两类:
- 回归
- 分类
回归算法的主要性能评估指标有:平均绝对误差(MAE)、平均平方误差(MSE)
分类算法的主要性能评估指标有:精确率、召回率、AUC曲线、ROC曲线等
1. 分类算法的性能评估指标
1.1 精确率与召回率
- 精确率是针对预测结果而言,预测结果为正的样本中有多少是真正为正的样本,也称为查准率
- 召回率是针对原本样本而言,样本中有多少正样本被预测为正样本,也称为查全率
| 定义 | 描述 |
|---|---|
| TP(True Positive,真正例) | 将正类预测为正类 |
| TN(True Negative,真负例) | 将负类预测为负类 |
| FP(False Positive,假正例) | 将负类预测为正类 |
| FN(False Negative,假负例) | 将正类预测为负类 |
根据定义,可知:
p e r c i s i o n = T P T P + F P percision = \frac{TP}{TP + FP} percision=TP+FPTP
r e c a l l = T P T P + F N recall = \frac{TP}{TP + FN} recall=TP+FNTP
应用场景:
(1)对于预测地震而言,我们更加看重的是召回率,希望每一次地震都可以被预测到;(2)对于垃圾邮件预测而言,我们更加看重精确率,被判断为垃圾邮件的要有很大把握才能判断为垃圾邮件;
1.2 F1-score
F1值就是精确值和召回率的调和均值(变量倒数的算术平均数的倒数)
2 F 1 = 1 P + 1 R \frac{2}{F_1} = \frac{1}{P} + \frac{1}{R} F12=P1+R1
即 F 1 = 2 P R P + R F_1 = \frac{2PR}{P+R} F1=P+R2PR
1.3 AUC与ROC
1.3.1 ROC曲线
接收者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,ROC曲线上每个点反映着对同一信号刺激的感受性。
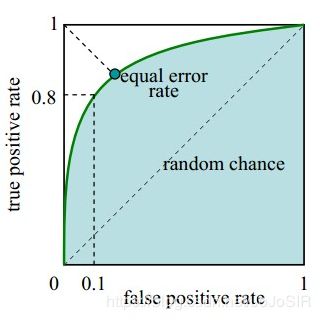
横坐标:1-Specificity,伪正类率(False positive rate,FPR,FPR=FP/(FP+TN)),预测为正但实际为负的样本占所有负例样本的比例;
纵坐标:Sensitivity,真正类率(True positive rate,TPR,TPR=TP/(TP+FN)),预测为正且实际为正的样本占所有正例样本的比例。
真正的理想情况,TPR应接近1,FPR接近0,即图中的(0,1)点。ROC曲线越靠拢(0,1)点,越偏离45度对角线越好。
1.3.2 AUC值
AUC (Area Under Curve) 被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
AUC值是一个概率值,当你随机挑选一个正样本以及负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值,AUC值越大,当前分类算法越有可能将正样本排在负样本前面,从而能够更好地分类。
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
1.3.3 为什么使用ROC和AUC
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变换的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡,即正负样本比例差距较大,而且测试数据中的正负样本也可能随着时间变化。下图是ROC曲线和Presision-Recall曲线的对比:
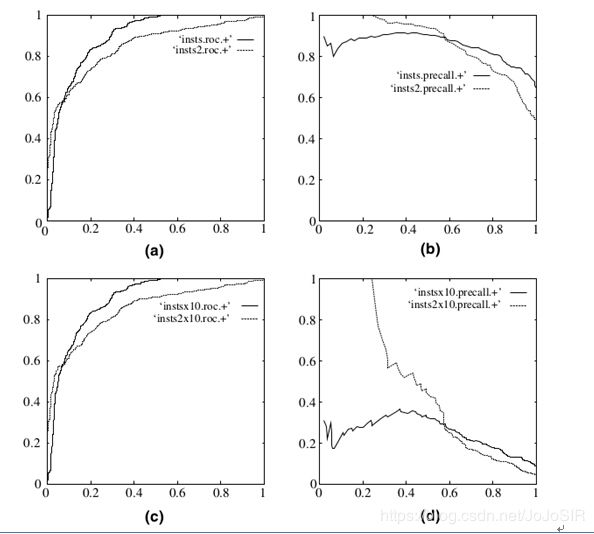
在上图中,(a)和(c)为Roc曲线,(b)和(d)为Precision-Recall曲线。
(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果,可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线变化较大。
样本不平衡的情况下具有评估优势。
2. 回归算法的性能评估指标
2.1 平均绝对误差(MAE)
平均绝对误差(MAE)就是指预测值与真实值之间平均相差多大。
M A E = 1 n ∑ i = 1 n ∣ f ( x i ) − y i ∣ MAE = \frac{1}{n}\sum_{i = 1}^{n} \left | f\left ( x_i \right ) - y_i \right | MAE=n1i=1∑n∣f(xi)−yi∣
2.2 平均平方误差(MSE)
均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE。MSE是衡量平均误差的一种较方便的方法,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
M S E = 1 n ∑ i = 1 n ( f ( x i ) − y i ) 2 MSE = \frac{1}{n}\sum_{i = 1}^{n}\left ( f\left ( x_i \right ) - y_i \right )^{2} MSE=n1i=1∑n(f(xi)−yi)2
MSE数值大小本身没有意义,随着样本增加,MSE必然增加,也就是说,不同的数据集的情况下,MSE比较没有意义
2.3 均方根误差(RMSE)
R M S E = 1 n ∑ i = 1 n ( f ( x i ) − y i ) 2 RMSE = \sqrt{\frac{1}{n}\sum_{i = 1}^{n}\left ( f\left ( x_i \right ) - y_i \right )^{2}} RMSE=n1i=1∑n(f(xi)−yi)2
2.4 决定系数(R2 score)
R 2 ( y , y ^ ) = 1 − ∑ i = 1 n ( y i − y i ^ ) 2 ∑ i = 1 n ( y i − y i ˉ ) 2 R^{2}\left ( y, \hat{y} \right ) = 1 - \frac{\sum_{i = 1}^{n}\left ( y_i - \hat{y_i} \right )^{2}}{\sum_{i = 1}^{n}\left ( y_i - \bar{y_i} \right )^{2}} R2(y,y^)=1−∑i=1n(yi−yiˉ)2∑i=1n(yi−yi^)2
- 数学理解: 分母理解为原始数据的离散程度,分子为预测数据和原始数据的误差,二者相除可以消除原始数据离散程度的影响
- 其实“决定系数”是通过数据的变化来表征一个拟合的好坏。
- 理论上取值范围(-∞,1], 正常取值范围为[0 1] ------实际操作中通常会选择拟合较好的曲线计算R²,因此很少出现-∞
越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好
越接近0,表明模型拟合的越差
经验值:>0.4, 拟合效果好
- 缺点:数据集的样本越大,R²越大,因此,不同数据集的模型结果比较会有一定的误差
2.5 交叉验证(cross-validation)
交叉验证,也称为循环估计。在给定的训练样本中,先拿出大部分样本进行建模,留小部分样本用刚建立的模型进行预测,并求这小部分样本的预测误差平方和。这个过程循环进行。把每个样本的预测误差平方相加,称为PRESS(predicted error sum of squares)。
交叉验证的基本思想是在某种意义下将原始数据进行分组,一部分用作训练集,另一部分用作测试集,首先用训练集对模型进行训练,然后用测试集对训练好的模型进行测试,以此来作为评价回归模型的性能指标。