基于图的推荐算法及python实现

概述

基于图的模型（graph-based model）是推荐系统中的重要内容。
在推荐系统中，用户行为数据可以表示成图的形式,具体地，可以用二元组 (u,i) ( u , i ) 表示，其中每个二元组 (u,i) ( u , i ) 表示用户 u u 对物品 i i 的产生过行为，这种数据很容易用一个二分图表示

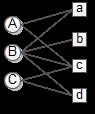
其中users集 U={A,B,C} U = { A , B , C } , items集 I={a,b,c,d} I = { a , b , c , d } 。我们用 G(V,E) G ( V , E ) 来表示上图。 V=U⋃I V = U ⋃ I ，图中的边则是由数据集中的二元组确定。本文不考虑各边的权重( u u 对 i i 的兴趣度)，都默认为1。

与pagerank算法的区别

有了图之后我们要对u进行推荐物品，就转化为计算用户顶点u和与所有物品顶点之间的相关性，按照相关性的高低生成推荐列表。说白了，这是一个图上的排名问题，我们最容易想到的就是Google的pageRank算法。这里只给出迭代公式，Pagerank算法的具体细节在此不做赘述，具体的可以看http://blog.csdn.net/john_xyz/article/details/78915097。

PR(i)=1−αn+α∑j∈(i)PR(j)out(j) P R ( i ) = 1 − α n + α ∑ j ∈ ( i ) P R ( j ) o u t ( j )

上式中 PR(i) P R ( i ) 是网页i的访问概率（也就是重要度）， α α 是用户继续访问网页的概率， n n 是网页总数。 in(i) i n ( i ) 表示指向网页i的网页集合， out(j) o u t ( j ) 表示网页j指向的网页集合。

与PageRank随机选择一个点开始游走（也就是说从每个点开始的概率都是相同的）不同，如果我们要计算所有节点相对于用户 u u 的相关度，则PersonalRank从用户 u u 对应的节点开始游走，每到一个节点都以 1−α 1 − α 的概率停止游走并从 u u 重新开始，或者以 α α 的概率继续游走，从当前节点指向的节点中按照均匀分布随机选择一个节点往下游走。这样经过很多轮游走之后，每个顶点被访问到的概率也会收敛趋于稳定，这个时候我们就可以用概率来进行排名了。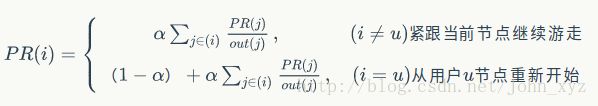

在执行算法之前，我们需要初始化每个节点的初始概率值。如果我们对用户 u u 进行推荐，则令 u u 对应的节点的初始访问概率为1，其他节点的初始访问概率为0，然后再使用迭代公式计算。而对于pageRank来说，由于每个节点的初始访问概率相同，所以所有节点的初始访问概率都是 1/n 1 / n （ n n 是节点总数）。

Python代码实现

分别用两种方式实现PersonalRank算法，一种是用纯粹的for循环去做，另外一种是用矩阵乘法。对于大规模稀疏矩阵 M M ，使用稀疏矩阵乘法相比于for循环，能提高上百倍的效率。当然，如果对于大规模数据使用稠密矩阵，依然很慢。

# coding:utf-8
import numpy as np
import time
import scipy.sparse as sparse
import pandas as pd

def PersonalRank(G, alpha, root):
    """
    Random walk algorithm：calculate importance of all nodes in respect to
    the start_node
    :param G: graph
    :param alpha: probability of random walkRa
    :param root: start node of random walk
    :param num_iter: nums of iteration
    :return: type of dict, ex.
    {node1:prob1, node2:prob2,...}
    """
    rank = dict()
    rank = {x:0 for x in G.keys()}
    rank[root] = 1
    pre = np.zeros(n)
    # iteration
    while np.sum(abs(np.array(list(pre)) - np.array(list(rank.values())))) > 0.001:
        # initialize
        pre = rank.values()
        tmp = {x:0 for x in G.keys()}
        # 取节点i和它的出边尾节点集合ri
        for i, ri in G.items():
            for j in ri:
                try:
                    tmp[j] += alpha * rank[i] / (1.0 * len(ri))
                except:
                    continue
        tmp[root] += (1 - alpha)
        rank = tmp
    result = sorted(rank.items(), key=lambda x:x[1], reverse=True)[:num_candidates]
    return result

def PersonalRankInMatrix(M, alpha, root):
    """
    Personal Rank in matrix formation
    :param M: transfer probability matrix
    :param index2node: index2node dictionary
    :param node2index: node2index dictionary
    :return:type of list of tuple, ex.
    [(node1, prob1),(node2, prob2),...]
    """
    result = dict()
    v = np.zeros(n)
    v[node2index[root]] = 1
    v0 = v
    while np.sum(abs(v - (alpha*M.dot(v) + (1-alpha)*v0))) > 0.001:
        v = alpha * M.dot(v) + (1-alpha)*v0
    for ind, prob in enumerate(v):
        result[index2node[ind]] =  prob
    result = sorted(result.items(), key=lambda x:x[1], reverse=True)[:num_candidates]
    return result

def Generate_Transfer_Matrix(G):
    """generate transfer matrix given graph"""
    index2node = dict()
    node2index = dict()
    for index,node in enumerate(G.keys()):
        node2index[node] = index
        index2node[index] = node
    # num of nodes
    n = len(node2index)
    # generate Transfer probability matrix, shape of (n,n)
    M = np.zeros([n,n])
    for node1 in G.keys():
        for node2 in G[node1]:
            # FIXME: some nodes not in the Graphs.keys, may incur some errors
            try:
                M[node2index[node2],node2index[node1]] = 1/len(G[node1])
            except:
                continue
    return M, node2index, index2node

def Generate_Transfer_SparseMatrix(G):
    """
    generate transfer sparse matrix given graph
    :param G: graph, type of dict
    :return: transfer matrix, type of 'scipy.sparse.coo.coo_matrix'
    """
    index2node = dict()
    node2index = dict()
    for index,node in enumerate(G.keys()):
        node2index[node] = index
        index2node[index] = node
    # num of nodes
    n = len(node2index)
    # initialize rows and columns
    rows = []
    columns = []
    data = []
    # generate Transfer probability Sparse matrix, shape of (n,n)
    for node1 in G.keys():
        for node2 in G[node1]:
            # FIXME: some nodes not in the Graphs.keys, may incur some errors
            try:
                rows.append(node2index[node2])
                columns.append(node2index[node1])
                data.append(1/len(G[node1]))
            except:
                continue
    rows = np.array(rows)
    columns = np.array(columns)
    data = np.array(data)
    M = sparse.coo_matrix((data, (rows,columns)),shape=(n,n))
    return M, node2index, index2node


# test algorithm performance
if __name__ == '__main__':
    alpha = 0.85
    root = 'A'
    num_iter = 100
    num_candidates = 10
    G = {'A' : {'a' : 1, 'c' : 1},
         'B' : {'a' : 1, 'b' : 1, 'c':1, 'd':1},
         'C' : {'c' : 1, 'd' : 1},
         'a' : {'A' : 1, 'B' : 1},
         'b' : {'B' : 1},
         'c' : {'A' : 1, 'B' : 1, 'C':1},
         'd' : {'B' : 1, 'C' : 1}}
    M, node2index, index2node = Generate_Transfer_SparseMatrix(G)
    n = len(M)
    print(pd.DataFrame(M, index=G.keys(), columns=G.keys()))
    time1 = time.time()
    result1 = PersonalRank(G, alpha, root)
    time2 = time.time()
    result2 = PersonalRankInMatrix(M, alpha, root)
    time3 = time.time()
    print(result1)
    print(result2)
    print(time2 - time1, time3 - time2)

关于稀疏矩阵的思考

在python中，可以借助官方库scipy.sparse和numpy中的dot和实现稀疏矩阵和稠密矩阵的相乘，具体如下

import numpy as np
import scipy.sparse as sparse

r=np.array([0,3,1,2,6,3,6,3,4])
c=np.array([0,0,2,2,2,4,5,6,3])
data=np.array([1,1,1,1,1,1,1,1,1])

a = np.ones(7)

sparse_matrix =sparse.coo_matrix((data, (r,c)), shape=(7,7))

print(sparse_matrix)
print(sparse_matrix.todense())
M = sparse_matrix.dot(a)

print(M)

reference

http://blog.csdn.net/gamer_gyt/article/details/51694250
http://blog.csdn.net/harryhuang1990/article/details/10048383