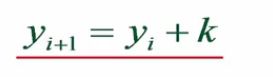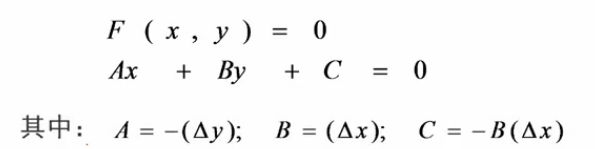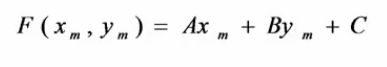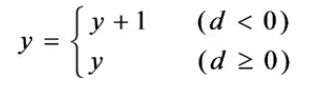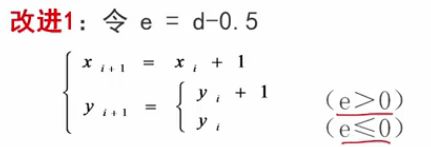计算机图形学 学习笔记（一）：概述，直线扫描转换算法：DDA，中点画线算法，Bresenham算法
前言
本笔记基于
http://www.icourse163.org/learn/CAU-45006?tid=1001746004#/learn/announce
感谢中国农大 赵明老师的分享~
现在我要为我自己走向游戏编程打下基石~
1 计算机图形学概论
1.1 计算机图形学课程简介
《计算机图形学》是计算机、地理信息系统、应用数学、机械、建筑等专业本科教学中的一门重要的专业基础课
如图像处理、模式识别、多媒体技术、计算机视觉等的基础
在CAD/CAM、计算机动画、系统环境模拟、地理信息系统、计算机艺术、真实感图形显示、科学计算的可视化、3D打印的等领域都有重要的应用
该门课程使学生了解计算机图形学的发展、掌握图形学的基本原理、算法和实现技术。学会基本的图形软件开发技术，为进一步学习后续课程打下良好的基础。
参考书籍：
- 《计算机图形学基础课程》 孙家广、胡事民，清华出版社
- 《计算机图形学（OpenGL版）（第3版）》胡事民，刘永进等 清华大学出版社
- 《计算机图形学基础》 陆枫、何云峰 电子出版社
- 《计算机辅助设计与图形学学报》
- 《中国图像图形学报》
1.2 计算机图形学概述
计算机图形学定义
简单来说，计算机图形是计算机产生的图像。
定义：计算机图形学就是研究如何在计算机中表示图形、以及利用计算机进行图形的计算、处理和显示的相关原理与算法
计算机图形学研究内容
如何在计算机中表示图形、以及利用计算机进行图形的计算、处理和显示的相关原理与算法，构成了计算机图形学的主要研究内容。
图形硬件：研究图形要有基本的支撑硬件，包括图形加速卡、显示器、图形输出设备等等。
一般来说，要在计算机上生成一副表示物体的图形，有三个步骤
造型技术
在计算机中建立索要生成图像的物体的模型，即给出表示该物体的集合数据和拓扑关系。光照模型
自然光照现象是由一些物理学定律所决定的，而这些物理学定律又非常复杂
所以，希望用一些简单的数学模型来近似、代替那些物理学的模型，为模拟物体表面的光照物理现象的数学模型叫光照模型绘制（渲染）技术
第三步是选择适当的绘制算法来把这个场景画（渲染）出来。就是将模型真实性显示在屏幕上。
渲染一幅三维物体图像所涉及的知识、实际上就是计算机图形中每个像素看上去应该是什么颜色的问题。这很大程度上取决于不同的光照模型。
计算机屏幕是由像素构成的，像素作为构成图形的基本单位。为了在屏幕上显示一幅图形，就必须研究在哪些像素上生成图形，就必须有一套针对光栅显示器生成图形的算法。
计算机图形学发展历史
要了解一门学科的发展，最好的就是了解它的发展历史
（百度去吧少年们）
计算机图形学的应用领域
- 人机交互和图形用户界面
- 计算机辅助设计与制造（CAD/CAM）
- 真实感图形绘制与自然景物方针
- 计算机游戏、电影、动漫
- 计算机艺术
- 计算机方针
- 科学计算可视化
- 虚拟现实
- 地理信息系统（GIS）
- 农业领域的应用
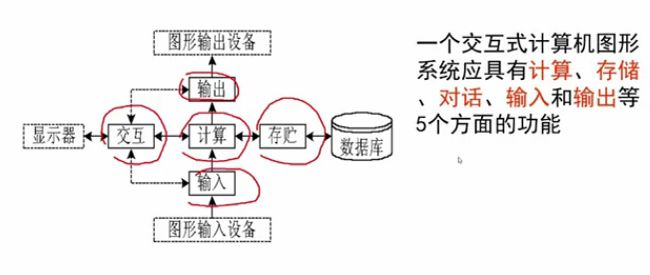
计算机图形处理系统组成
2 光栅图形学算法
随着光栅显示器的出现，为了在计算机上处理、显示图形，需要发展一套与之相适应的算法：光栅图形学算法。
光栅图形算法多数属于计算机图形的底层算法，很多图形学的基本概念和思想都在这一章。
光栅图形学算法的研究内容
- 直线段的扫描转换算法
- 多边形的扫描转换与区域填充算法
- 裁剪算法
- 反走样算法
- 消隐算法
2.1 直线段的扫描转换算法—DDA
在数学上，直线上的点有无穷多个。但当在计算机光栅显示器屏幕上表示这条直线时需要做一些处理（因为光栅显示器是由一个个像素点构成的，而像素又是有限的）
为了在光栅显示器上用有限的点逼近无限的点构成的直线，需要知道这些像素点的x,y坐标
DDA画线算法 1
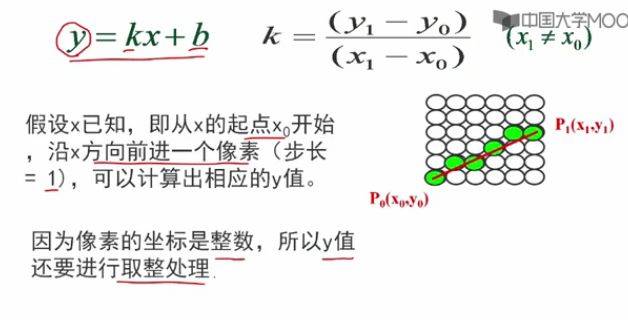
如何把数学上的一个点扫描转换成一个频幕像素点？（因为像素点都是整数，所以我要对点进行取整处理，x和y都要是整数）
y=kx+b
直线是最基本的图形，一个动画或真实感图形往往需要调用成千上万次画线程序，因此直线算法的好坏与效率将直接影响图形的质量和显示速度。
回顾一下刚才的算法：
y=kx+b（直线斜截式方程）
这个算法，有乘法运算和加法运算，还有后期的取整运算。
为了提高效率，把计算量减下来，关键问题就是如何把乘法取消？（因为计算机中加减乘除，加法的运算效率最快）
DDA画线算法 2
为了提高效率，把乘法取消。我们需要学习三个著名的常用算法。
直线绘制的三个著名的常用算法
- 数值微分法（DDA）
- 中点画线法
- Bresenham算法
一、数值微分法DDA
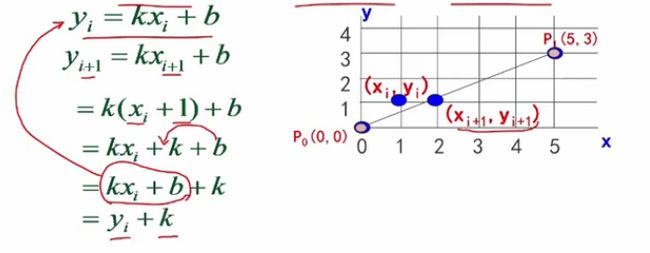
引进图形学中一个很重要的思想—增量思想。
注：之所以能写成
是因为数学上的点要转换成像素点，因此x和y都是整数，而像素最小的单位为1，直线肯定的点与点之间肯定不会隔多远，因此默认相隔一个像素
这样也就是说
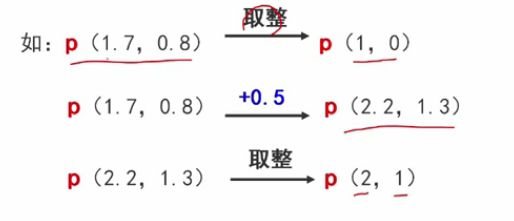
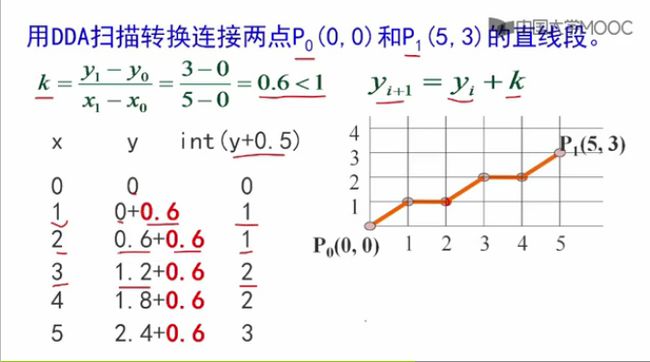
例子：
【思考题】
DDA画直线算法：x每递增1，y递增斜率k。是否适合任意斜率的直线？
（1） | k | <= 1 时，
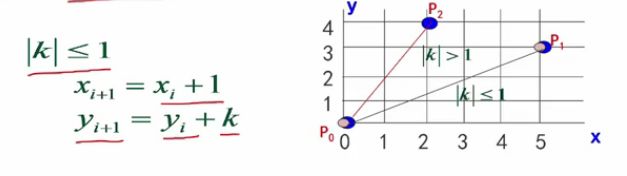
（2） | k | > 1 时，
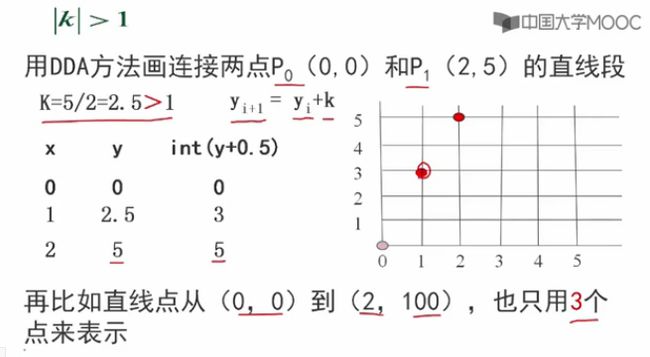
如果K>1，会导致光栅点太稀了！
除开起点和终点，中间只有1个点，而1个点完全无法表达直线的趋势。
那么如何解决K>1时的直线扫描算法呢？
2.2 直线段的扫描转换算法—中点画线
采用增量思想的DDA算法，直观、易实现，每计算一个像素坐标，只需计算一个加法。
这个算法是否最优呢？若非最优，如何改进？
（我们在2.1中已经知道DDA不适合于斜率k>1的情况）
（1）改进效率
这个算法每步只做一个加法，能否再提高效率呢？
计算机运行最快的就是加法。
但是加法分为整数加法和浮点加法。
一般情况下k与k都是小数，而且每一步运算都要对y进行四舍五入后取整。
唯一改进的途径就是把浮点运算变成整数加法。
（2）改善直线方程类型
这样就引出了中点画线算法~~~
中点画线算法 1
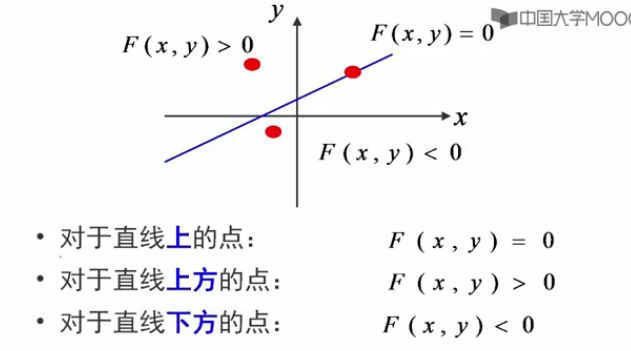
直线的一般式方程：
这个方程把屏幕分成3部分
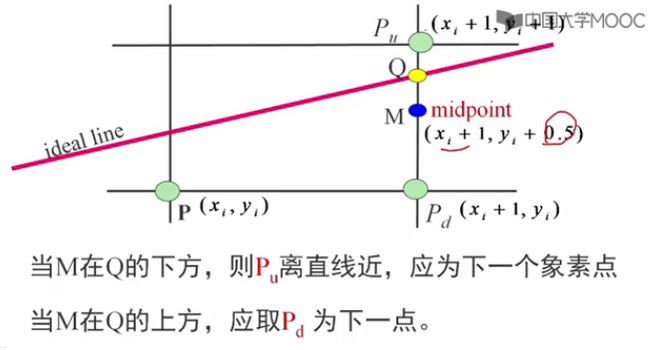
思想：每次在最大位移方向（最大位移发现就是+1，到达屏幕的另一部分）上走一步，而另一个方向是走还是不走要取决于中点误差项的判断（两个方向就x和y）。
假定：0<=| k |<=1。因此，每次在x方向上加1，y方向上加1或不变需要判断。
如何判断Q在M的上方还是下方呢？
把M的坐标代入理想直线方程：
假如M的坐标为d(i)
下面来分析一个中点画线算法的计算量
虽然中点画线算法解决了斜率大于1时，DDA算法不精确的问题。
但明显的是这个计算量就比DDA大多了（DDA是1个乘法1个加法）
那么能否也采用增量计算，提高计算效率呢？
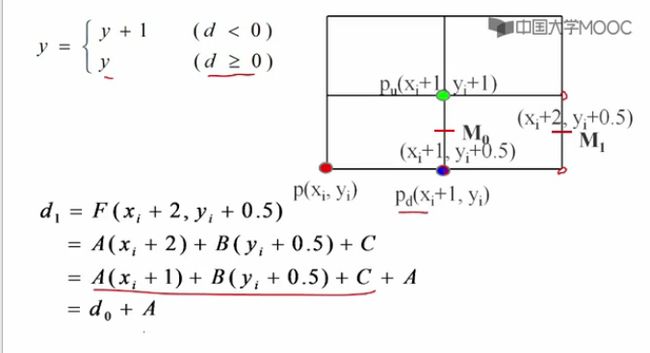
中点画线算法 2
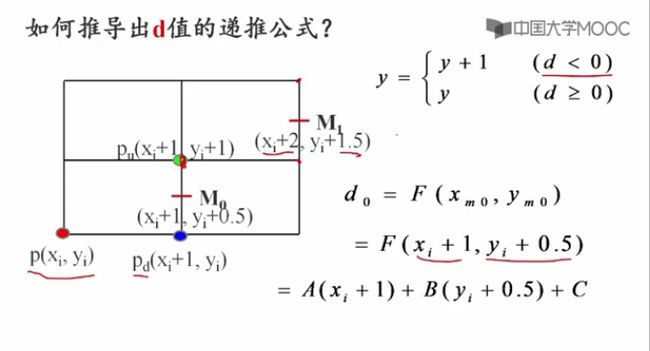
如何推导出d值得递推公式？
（1）d<0 的情况下
（2）d>0 的情况下
下面计算d的初始值d[0]
完整的中点画线算法
【小结】
- 中点画线算法采用直线一般式方程，而DDA采用斜截式方程
- 通过判断中点额符号，最终可以只进行整数加法
这个算法是否还有改进的余地？
2.3 直线段的扫描转换算法—Bresenham算法
中点画线法
这个算法是否还有改进的余地？
从计算机的运算效率来说。中点画线只做一个整数加法，而整数加法已经是最快的了。
那么只能从直线的方程入手。
能否提出一个算法，使这个算法不但能解决画直线，还能解决圆弧、抛物线甚至自由曲线的光栅化问题，使算法的覆盖域扩大。
这就引出了Bresenham算法。
Bresenham算法 1
DDA把算法效率提高到每步只做一个加法。（加法中间有乘法运算）
中点算法进一步把效率提高到每步只做一个整数加法。
Bresenham算法提供了一个更一般的算法。该算法不仅有好的效率，而且有更广泛的适用范围。
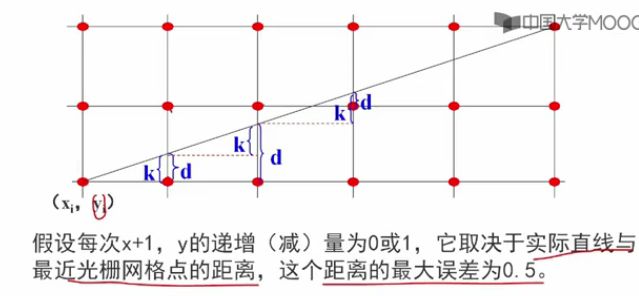
Bresenham算法的基本思想
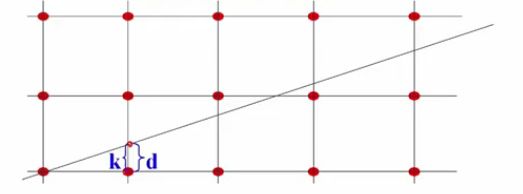
该算法的思想是通过各行、各列像素中心构造一组虚拟网络线，按照直线起点到终点的顺序，计算直线与各垂直网格线的交点，然后根据误差项的符号确定该列像素中与此交点最近的像素。
Bresenham算法 2
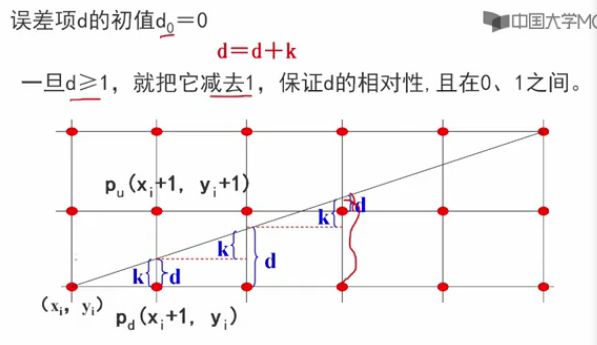
（1）改进e
（2）改进 e初 和 k
算法步骤为：
Bresenham算法很像DDA算法，都是加斜率。
但DDA算法使判断符号来决定上下两个点。所以该算法集中DDA和终点两个算法的优点，而且应用范围广泛。
【小结】
- 计算机科学问题的核心就是算法
- 领会算法中所蕴含的创新思想
- 科学研究无止境，学术面前人人平等