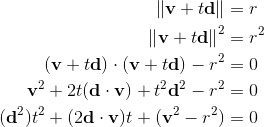光线跟踪(RayTracing)原理及c++实现

Chapt1. Why to write a RayTracing Render

提到Computer Graphics，众所周知的是如OpenGL、Direct3D这样非常流行的光栅化渲染器。事实上，这些大部分应用于游戏制作的API主要为实时渲染（Real-time Rendering）而设置，而它们所采用的光栅化(Rasterization)的渲染方式，通过渲染大量的三角形（或者其他的几何图元种类(Primitive types)），是与本文介绍的光线跟踪相对的一种渲染方式。这种基于光栅化的渲染系统，往往只支持局部照明(Local Illumination)。局部照明在渲染几何图形的一个像素时，光照计算只能取得该像素的信息，而不能访问其他几何图形的信息。

图1.jpg

该图片出自《孤岛惊魂》，尽管看似水面显示出了远处山峰的倒影，却不能渲染植被、船骸等细节。

理论上，阴影(Shadow)、反射(Reflection)、折射(Refraction)均为全局照明(Global Illumination)效果，所以在实际应用中，栅格化渲染系统可以使用预处理(如阴影贴图(shadow mapping)、环境贴图(environment mapping))去模拟这些效果。

栅格化的最大优势是计算量比较小，适合实时渲染。相反，全局光照计算量大，一般也没有特殊硬件加速(通常只使用CPU而非GPU)，所以只适合离线渲染(offline rendering)，例如3D Studio Max、Maya等工具。其中一个支持全局光照的方法，称为光线追踪(ray tracing)。光线追踪能简单直接地支持阴影、反射、折射，实现起来亦非常容易。

Chapt2. Principles of RayTracing

由光源发出的光到达物体表面后，产生反射和折射，简单光照明模型和光透射模型模拟了这两种现象。在简单光照明模型中，反射被分为理想漫反射和镜面反射光，把透射光模型分为理想漫透射光和规则透射光。由广元发出的光成为直接光，物体对直接光的反射或折射成为直接反射和直接折射，相对的，把物体表面间对广德反射和折射成为间接光、间接反射、间接折射。光线在物体之间的传播方式是光线跟踪算法的基础。

最基本的光线跟踪算法是跟踪镜面反射和折射。从光源发出的光遇到物体的表面，发生反射和折射，光就改变方向，沿着反射方向和折射方向继续前进，知道遇到新的物体。但是光源发出光线，经过反射与折射，只有很少部分可以进入人的眼睛。因此实际光线跟踪算法的跟踪方向与光传播的方向是相反的（反向光线跟踪），称之为视线跟踪。由视点与像素(x,y)发出一根射线，与第一个物体相交后，在其反射与折射方向上进行跟踪，如图2所示

图2.gif

在光线跟踪算法中，我们有如下的四种光线：

• 视线是由视点与像素(x，y)发出的射线；
• 阴影测试线是物体表面上点与光源的连线；
• 反射光线；
• 折射光线

当光线 V与物体表面交于点P时，点P分为三部分，把这三部分光强相加，就是该条光线V在P点处的总的光强：

• a) 由光源产生的直接的光线照射光强，是交点处的局部光强，可以由下式计算：
  
  
  

  式1.gif

---

• b) 反射方向上由其它物体引起的间接光照光强，由IsKs' 计算，Is通过对反射光线的递归跟踪得到
• c) 折射方向上由其它物体引起的间接光照光强，由ItKt' 计算，It通过对折射光线的递归跟踪得到

现在我们来讨论光线跟踪算法本身。我们将对一个由两个透明球和一个非透明物体组成的场景进行光线跟踪（图3）通过这个例子，可以把光线跟踪的基本过程解释清楚。

图3.gif

在我们的场景中，有一个点光源L，两个透明的球体O1与O2，一个不透明的物体O3。首先，从视点出发经过视屏一个像素点的视线E传播到达球体O1，与其交点为P1。从P1向光源L作一条阴影测试线S1，我们发现其间没有遮挡的物体，那么我们就用局部光照明模型计算光源对P1在其视线E的方向上的光强，作为该点的局部光强。同时我们还要跟踪该点处反射光线R1和折射光线T1，它们也对P1点的光强有贡献。在反射光线R1方向上，没有再与其他物体相交，那么就设该方向的光强为零，并结束这光线方向的跟踪。然后我们来对折射光线T1方向进行跟踪，来计算该光线的光强贡献。折射光线T1在物体O1内部传播，与O1相交于点P2，由于该点在物体内部，我们假设它的局部光强为零，同时，产生了反射光线R2和折射光线T2，在反射光线R2方向，我们可以继续递归跟踪下去计算它的光强，在这里就不再继续下去了。我们将继续对折射光线T2进行跟踪。T2与物体O3交于点P3，作P3与光源L的阴影测试线S3，没有物体遮挡，那么计算该处的局部光强，由于该物体是非透明的，那么我们可以继续跟踪反射光线R3方向的光强，结合局部光强，来得到P3处的光强。反射光线R3的跟踪与前面的过程类似，算法可以递归的进行下去。重复上面的过程，直到光线满足跟踪终止条件。这样我们就可以得到视屏上的一个象素点的光强，也就是它相应的颜色值。

上面的例子就是光线跟踪算法的基本过程，我们可以看出，光线跟踪算法实际上是光照明物理过程的近似逆过程，这一过程可以跟踪物体间的镜面反射光线和规则透射，模拟了理想表面的光的传播。

虽然在理想情况下，光线可以在物体之间进行无限的反射和折射，但是在实际的算法进行过程中，我们不可能进行无穷的光线跟踪，因而需要给出一些跟踪的终止条件。在算法应用的意义上，可以有以下的几种终止条件：

• 该光线未碰到任何物体。
• 该光线碰到了背景
• 光线在经过许多次反射和折射以后，就会产生衰减，光线对于视点的光强贡献很小（小于某个设定值）
• 光线反射或折射次数即跟踪深度大于一定值

Chapt3. Rasterization & RayTracing

了解了光线跟踪的原理之后，再来看一下在计算机上的实现。

光栅化渲染，简单地说，就是把大量三角形画到屏幕上。当中会采用深度缓冲(depth buffer, z-buffer)，来解决多个三角形重叠时的前后问题。三角形数目影响效能，但三角形在屏幕上的总面积才是主要瓶颈。

光线追踪，简单地说，就是从摄影机的位置，通过影像平面上的像素位置(比较正确的说法是取样(sampling)位置)，发射一束光线到场景，求光线和几何图形间最近的交点，再求该交点的著色。如果该交点的材质是反射性的，可以在该交点向反射方向继续追踪。光线追踪除了容易支持一些全局光照效果外，亦不局限于三角形作为几何图形的单位。任何几何图形，能与一束光线计算交点(intersection point)，就能支持。

图4.png

上图显示了光线追踪的基本方式。要计算一点是否在阴影之内，也只须发射一束光线到光源，检测中间是否存在障碍物。

Chapt4. Source Code

1. Base Class

本例代码尝试使用基于物件(object-based)的方式编写

3D Vector

struct Vector {
    float x, y, z;
    Vector(float x_, float y_, float z_) : x(x_), y(y_), z(z_) {}
    Vector(const Vector& r) : x(r.x), y(r.y), z(r.z) {}
    float sqrLength() const {
        return x  x + y  y + z  z;
    }
    float length() const {
        return sqrt(sqrLength());
    }
    Vector operator+(const Vector& r) const {
        return Vector(x + r.x, y + r.y, z + r.z);
    }
    Vector operator-(const Vector& r) const {
        return Vector(x - r.x, y - r.y, z - r.z);
    }
    Vector operator(float v) const {
        return Vector(v  x, v  y, v  z);
    }
    Vector operator/(float v) const {
        float inv = 1 / v;
        return this  inv;
    }
    Vector normalize() const {
        float invlen = 1 / length();
        return this  invlen;
    }
    float dot(const Vector& r) const {
        return x  r.x + y  r.y + z  r.z;
    }
    Vector cross(const Vector& r) const {
        return Vector(-z  r.y + y  r.z,
                      z  r.x - x  r.z,
                      -y  r.x + x  r.y);
    }
    static Vector zero() {
        return Vector(0, 0, 0);
    }
};
inline Vector operator(float l, const Vector& r) {return r  l;}

这些类方法(如normalize、dot、cross等)，如果传回Vector对象，都会传回一个新建构的Vector。这些三维向量的功能很简单，不在此详述。

Vector zero()用作常量，避免每次重新构建。值得一提，这些常量必需在prototype设定之后才能定义。

Ray

即为光线类，所谓光线(ray)，从一点向某方向发射也。数学上可用参数函数(parametric function)表示：

式2.png

当中，o即发谢起点(origin)，d为方向。在本文的例子里，都假设d为单位向量(unit vector)，因此t为距离。实现如下

struct Ray {
    Vector origin, direction;
    Ray(const Vector& o, const Vector& d) : origin(o), direction(d) {}
    Vector getPoint(float t) const {
        return origin + t * direction;
    }
};

Sphere

球体(sphere)是其中一个最简单的立体几何图形。这里只考虑球体的表面(surface)，中心点为c、半径为r的球体表面可用等式(equation)表示：

式3.png

如前文所述，需要计算光线和球体的最近交点。只要把光线x = r(t)代入球体等式，把该等式求解就是交点。为简化方程，设v=o - c，则:

式4.png

因为d为单位向量，所以二次方的系数可以消去。 t的二次方程式的解为

式5.png

struct Sphere : public Geometry {
    Vector center;
    float radius, sqrRadius;
    Sphere(const Vector& c, float r, Material m = NULL) :
            Geometry(m), center(c), radius(r), sqrRadius(r  r) {}
    IntersectResult intersect(const Ray& ray) const {
        Vector v = ray.origin - center;
        float a0 = v.sqrLength() - sqrRadius;
        float DdotV = ray.direction.dot(v);
        if (DdotV <= 0.0) {
            float discr = DdotV * DdotV - a0;
            if (discr >= 0.0) {
                float d = -DdotV - sqrt(discr);
                Vector p = ray.getPoint(d);
                Vector n = (p - center).normalize();
                return IntersectResult(this, d, p, n);
            }
        }
        return IntersectResult();
    }
};