python实现Floyd算法

'''这两天看了不少讲Floyd算法的文章，大概理解了其中的思想
然后自己动手，从图和节点类的定义开始，整个自己写了一下
和其他博主的实现方式上会有一些差别，注释我都写上了，有问题期待交流'''

class Vertex():
    def __init__(self,key):
        self.id = key #存储节点名称
        self.connectedTo = {} #存储相邻节点信息

    def addNeighbor(self,nbr,weight = 0):
        self.connectedTo[nbr] = weight #添加相邻节点
        #nbr.connectedTo[self] = weight #实现双向互通

    def getConnections(self):
        return self.connectedTo.keys() #返回所有相邻节点的信息

    def getId(self):
        return self.id #返回当前节点的名称

    def getWeight(self,nbr):
        if nbr not in self.connectedTo.keys() and nbr!=self:
            return 99999
        elif nbr == self:
            return 0
        else:
            return self.connectedTo[nbr]  #返回指定相邻节点的权重


    def __str__(self):
        return str(self.getId()) + 'connected to' +str([x.getId() for x in self.connectedTo.keys()])#打印时返回节点的连接信息

class Graph():
    def __init__(self):
        self.verList = {} #以字典的形式存储节点和节点对象
        self.size = 0 #图的大小

    def addVertex(self,key):
        '''向图中添加节点'''
        self.verList[key] = Vertex(key)
        self.size += 1

    def getVertex(self,key):
        '''返回节点信息'''
        if key in self.verList.keys():
            return self.verList[key]
        else:
            return False

    def __contains__(self, key):
        return key in self.verList.keys() #判断节点是否在图中

    def addEdge(self,fromV,toV,cost = 0):
        '''向图中添加一条边'''
        if fromV not in self.verList.keys():
            self.addVertex(fromV)
        if toV not in self.verList.keys():
            self.addVertex(toV)

        self.verList[fromV].addNeighbor(self.verList[toV],weight = cost)

    def getVertice(self):
        return self.verList.keys() #返回节点列表

    def __iter__(self):
        return iter(self.verList.values())

#开始创建图

g = Graph()
for i in range(1,5):
    g.addVertex(i)
g.addEdge(1,2,2)
g.addEdge(1,3,6)
g.addEdge(1,4,4)
g.addEdge(2,3,3)
g.addEdge(3,1,7)
g.addEdge(3,4,1)
g.addEdge(4,3,12)
g.addEdge(4,1,5)


#先构建一个邻接矩阵来存放任意两点之间的距离
dis = []
for i in g:
    temp = []
    for v in g:
        temp.append(i.getWeight(v))
    dis.append(temp)

print(dis)

#当只允许通过节点1时

for i in g:
    for v in g:
        #如果以1为中转点的距离小于原始距离
        if dis[i.getId()-1][v.getId()-1] > dis[i.getId()-1][0]+dis[0][v.getId()-1]:
            dis[i.getId() - 1][v.getId() - 1] = dis[i.getId() - 1][0] + dis[0][v.getId() - 1]
print(dis)


#经过所有顶点

for k in g:
    for i in g:
        for v in g:
            # 如果经过中转点的距离小于原始距离
            if dis[i.getId() - 1][v.getId() - 1] > dis[i.getId() - 1][k.getId()-1] + dis[k.getId()-1][v.getId() - 1]:
                dis[i.getId() - 1][v.getId() - 1] = dis[i.getId() - 1][k.getId()-1] + dis[k.getId()-1][v.getId() - 1]

print(dis)


#看算法效果
#原始距离
'''[[0, 2, 6, 4], [99999, 0, 3, 99999], [7, 99999, 0, 1], [5, 99999, 12, 0]]'''
#只经过顶点1的距离
'''[[0, 2, 6, 4], [99999, 0, 3, 99999], [7, 9, 0, 1], [5, 7, 11, 0]]'''
#尝试所有顶点的最短距离
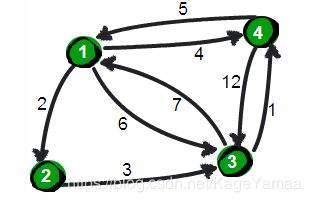
'''[[0, 2, 5, 4], [9, 0, 3, 4], [6, 8, 0, 1], [5, 7, 10, 0]]'''

文章代码实现的图是这样子的：

图非原创，来自于博主@Angel_Kitty，主页链接：https://www.cnblogs.com/ECJTUACM-873284962/p/6995648.html