平衡树总结
高级数据结构_平衡树学习笔记
本文章同步与我的Luogu博客。
学习平衡树的一些总结。
BST树,即二叉查找树,是一种数据结构,满足这样的条件:
一颗BST树的中序遍历是有序的。
例:
将{1,4,2,3,5,8,10,7}建成BST树:
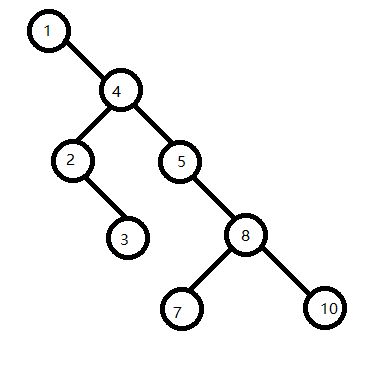
某同学:
BST树长得又丑,又不能节省空间,我干嘛要学它啊。
因为能省时间。
我们找到任意节点p,发现p的左子树中的任意节点都小于p,p的右子树中的任意节点都大于p。
有了这个性质,我们就可以来看一些关键操作了。
1.查找:
在BST上查找一个元素类似于二分查找。
设当前元素大小为q,带查找元素大小为k。
1.若k==q,直接返回
2.若k>q,向右子树递归
3.若k期望复杂度O(logn)。
int search(int k,int u)
{
if(!u)return 0;
if(k==val(u))return u;
if(k>val(u))return search(rs(u));
if(k简单明快。
2.插入:
插入也很简单,就是一个查找加上一个开点。
void new_point(int k,int u,int fa)
{
if(!tot){a[++tot]=node(0,0,k);root=tot;}
if(!u){a[++tot]=node(0,0,k);if(k>val(fa))rs(fa)=tot;else ls(fa)=tot;return;}
if(k>val(u))new_point(k,rs(u),u);
if(k<val(u))new_point(k,ls(u),u);
}
3.删除:
也简单,删除值为x的点也是一次查找…
找不到就作罢,找到了的话就分三种情况讨论。
1.当前点没有左右孩子,直接将其父亲的这个孩子清空。
2.当前点只有一个孩子,将那个孩子提到当前位置。
3.当前点有两个孩子,就将其左子树中的最大点置换到当前点的位置。
void del_point(int k,int u,int fa)
{
if(!u)return;
if(k==val(u))
{
if(!ls(u)&&!rs(u))if(k>val(fa))rs(fa)=0;else ls(fa)=0;
if(!ls(u))if(k>val(fa))rs(fa)=rs(u);else ls(fa)=rs(u);
if(!rs(u))if(k>val(fa))rs(fa)=ls(u);else ls(fa)=ls(u);
else
{
p=ls(u);while(rs(rs(p)))p=rs(p);
if(root==u)root=p;int fi=p;p=rs(p);
rs(fi)=ls(p);if(k>val(fa))rs(fa)=p;else ls(fa)=p;
}
}
if(k>val(u))del_point(k,rs(u),u);
if(k<val(u))del_point(k,ls(u),u);
}
我们知道,在树上操作的的时间复杂度多取决于树高。
正是因为如此,我们可以说我们的BST树的期望时间复杂度是O(logn)。
但是我们可以考虑如下情况:
向一颗BST树顺序插入{1,2,3,4,5,6,7,8}。
得到的树长这样:
这棵树退化为了一条链。
我们又不能决定输入顺序,怎么办呢?
这里介绍一个黑科技:AVL树。
AVL树就是我们常说的"高度平衡的树"。
我们引入一个概念:节点的平衡因子。
一个节点的平衡因子是它的左子树高减去它的右子树高。
AVL树是一颗空树或所有节点的平衡因子都为{-1,0,1}这三个数中的一个的一棵树。
这样就可以控制树高在logn附近。
怎么实现呢?
我们先考虑向一颗AVL中插入一个节点。
如图,插入元素导致一条链上的所有节点的平衡因子发生了变化。
上图是一个比较好的情况,插入元素没有对AVL树本身产生什么大的影响。
看下图:
这个时候,我们就考虑调整整棵树的结构来保持这一颗树的平衡性质。
调整的方法被称为平衡化旋转。
通过平衡化旋转,我们可以在不破坏二叉搜索树性质的前提下维持树的平衡性。
平衡化旋转只跟一个点沿修改的链向下两个点有关。
怎么转呢?我们来分类讨论一下:
1.三点一线向左:
2.三点一线向右:
3.中间点向左突出:
4.中间点向右突出:
左单旋:
void lrotate(int x,int y,int z)
{
int k=ls(y);
ls(y)=x;
rs(x)=k;
}
右单旋:
void rrotate(int x,int y,int z)
{
int k=rs(y);
rs(y)=x;
ls(x)=k;
}
左右双旋:
void lrrotate(int x,int y,int z)
{
ls(x)=z;
rs(y)=ls(z);
ls(z)=y;
rrotate(x,z,y);
}
右左双旋:
void rlrotate(int x,int y,int z)
{
rs(x)=z;
ls(y)=rs(z);
rs(z)=y;
lrotate(x,z,y);
}
在每一个函数末尾都添加上修复用函数:
void fix_up(int x,int y,int z)
{
if(x>y&&y>z)rrotate(x,y,z);
if(x<y&&y<z)lrotate(x,y,z);
if(x>z&&z>y)lrrotate(x,y,z);
if(x<z&&z<y)rlrotate(x,y,z);
}
平衡化旋转的实质就是压缩一条链的高度来改进搜索树的结构。
Splay树,又名伸展树是一种自平衡树。
严格上来说,splay树并不算是一棵高度平衡的树,但是它通过伸展操作(splay操作)来保持结构的高效性。
"伸展操作"的意思,是将一个特定的点转到特定的位置去。
一般用splay(x,T)代表将元素x旋转到splay树T的根结点处。
那么splay操作是怎么实现的呢?
还是基于平衡化旋转。
不过这个旋转不再是为了使树变得平衡,而是为了改变的节点的深度。
有两种基础的旋转:
Zig(右旋)和Zag(左旋)。
Zig:
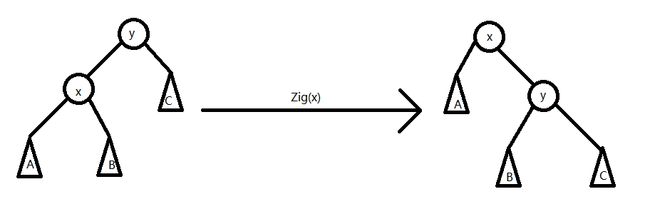
Zag:
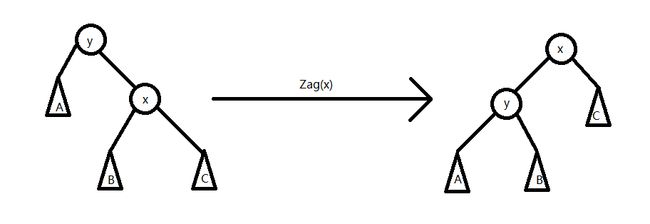
这就是最基本的伸展树上的平衡化旋转。
接下来我们就要介绍怎么将一个节点旋转到根上了。
进行分类讨论:
情况1:(Zig单旋)待旋转节点为x,其父亲y为树根,x为y的左孩子。
这个时候进行一次Zig(x),就可以将x旋转至根上。
情况2:(Zag单旋)待旋转节点为x,其父亲y为树根,x为y的右孩子。
这个时候进行一次Zig(x),就可以将x旋转至根上。
1,2互为逆操作。
情况3:(Zig-Zig双旋)待旋转节点x的父亲(y),祖父(z)同向左偏斜。
进行一次Zig(y),一次Zig(x),将x旋转到z处。
情况4:(Zag-Zag双旋)待旋转节点x的父亲(y),祖父(z)同向右偏斜。
进行一次Zag(y),一次Zag(x),将x旋转到z处。
3,4互为逆操作。
情况5:(Zig-Zag双旋)待旋转节点x是其父亲y的左孩子,y是其父亲z的右孩子。
进行一次Zig(x),一次Zag(x),将x旋转到z处。
情况6:(Zag-Zig双旋)待旋转节点x是其父亲y的右孩子,y是其父亲z的左孩子。
进行一次Zag(x),一次Zig(x),将x旋转到z处。
附加内容:用一个rotate函数代替Zig和Zag两个函数。
首先定义一个connect函数,规定connect(x,y,son)代表将x连接到y的son孩子上。
bool identify(int p){return p==rs(fa(p));}
void connect(int p,int f,int son){fa(p)=f;prp(f,son)=p;}
我们发现,Zig(x)中的x必定是左孩子,Zag(x)中的x必定是右孩子。
所以我们就可以用rotate(x)来代替左右旋转了。
void rotate(int p)
{
int y=fa(p);int mroot=fa(y);
int mson=identify(y);
int yson=identify(p);
int z=lft(p,yson);
connect(z,y,yson);
connect(y,p,yson^1);
connect(p,mroot,mson);
push_up(y);push_up(p);
}
有了前述知识,splay操作就很好理解了。
void splay(int p,int to)
{
to=fa(to);
while(sp[p].fa!=to)
{
int up=fa(p);
if(fa(up)==to)rotate(p);
else if(identify(p)==identify(up)){rotate(up);rotate(p);}
else{rotate(p);rotate(p);}
}
}
例题:
Luogu P3369 【模板】普通平衡树
来看看这个例题要我们实现的几个操作:
1.插入:
splay的插入就和普通的insert操作一样,只是需要将新加入的节点旋转到根上。
图示:
2.删除:
splay的删除就比较的玄学了。
简单来说,就是找到要删除的点(就是二叉查找树的搜索),将其旋转到根上,将其直接删除掉,再将其的左右孩子合并。
图示:
void push(int val){int add=insert(val);splay(add,root);}
int insert(int val)
{
if(tot==0){root=1;new_point(val,0);}
else
{
int p=root;
while(1)
{
sum(p)++;
if(val==val(p)){cnt(p)++;return p;}
int next=val<sp[p].val?0:1;
if(!prp(p,next))
{
new_point(val,p);
prp(p,next)=tot;
return tot;
}
p=sp[p].ch[next];
}
}
return 0;
}
3.查询某个数排名:
查询一个节点的排名,就是基本操作了。
简单来说,就是一次查找,找到比它大的就跳,找到比它小的就叠加size,找到一样的就输出。
记得查到结果了就splay一下,将节点旋到根。
int rank(int val)
{
sum(0)=0;
int ans=0,p=root;
while(1)
{
if(val(p)==val){int res=ans+sum(ls(p))+1;splay(p,root);return res;}
if(p==0) return 0;
if(val<val(p)) p=ls(p);
else{ans=ans+sum(ls(p))+cnt(p);p=rs(p);}
}
}
4.查询某个排名对应的数:
也是利用size域完成的。
,size够就向这一边跳,不够就往另一边,size符合就返回。
int atrank(int x)
{
int p=root;
while(1)
{
int minused=sum(p)-sum(rs(p));
if(x>sum(ls(p))&&x<=minused)break;
if(x<minused)p=ls(p);
else{x=x-minused;p=rs(p);}
}
splay(p,root);
return val(p);
}
5,6.查询前驱&&后继:
很简单。
将插入一个值为待查询值的点,将其splay到根上去,输出完了就删掉。
int lower(){int p=ls(root);while(rs(p))p=rs(p);return val(p);}
int upper(){int p=rs(root);while(ls(p))p=ls(p);return val(p);}
例题代码:
#includeThink Functional!
要学FHQ Treap,首先要理解什么是FHQ。
所谓的"FHQ",就是非旋的意思。
代表这种平衡树不需要依靠旋转来保持平衡。
事实上,FHQ Treap依靠分裂和合并来维持平衡性质。
所以我们称FHQ Treap为函数式Treap(即:不对现有的数据进行任何修改,仅仅是用历史数据来计算出新的)。
下面就来介绍一下这两个操作:
1.分裂:
所谓的"分裂",就是将一颗FHQ Treap分成两颗,每一颗都满足FHQ Treap的性质。
其实很简单,就是一个递归求解的过程。
定义split(p,k,&x,&y),代表将以p为根的子树分为两个部分,其根分别为x,y。
这种分裂应满足:
以x为根的FHQ Treap的size域不大于k。
图例:
void split(int p,int k,int &x,int &y)
{
if(!p){x=y=0;return;}
push_down(p);
if(tls(p).size<k){x=p;split(rs(x),k-tls(p).size-1,rs(x),y);}
else{y=p;split(ls(y),k,x,ls(y));}
push_up(p);
}
2.合并:
所谓的合并,就是将两颗FHQ Treap合为一颗。
也是一个递归的过程。
规定merge(x,y)返回的是将根为x,y的两棵树合并后的根。
图例:
int merge(int x,int y)
{
if(!x||!y)return x+y;
push_down(x);push_down(y);
if(t(x).rnd<t(y).rnd){rs(x)=merge(rs(x),y);push_up(x);return x;}
else{ls(y)=merge(x,ls(y));push_up(y);return y;}
}
例题:
Luogu P3391 【模板】文艺平衡树(Splay)
什么?你说题目要我们用Splay?不存在的。
就用FHQ Treap。
怎么支持区间翻转呢?
打标记,标记下传时swap左右子树。
代码:
#include这是一个题目:
Luogu P5055 【模板】可持久化文艺平衡树
是时候展现一下FHQ Treap的能力了
对于我们的所求,这一题的题目已经说的很清楚了。
在题解的正题开始之前,先放几个链接:
Luogu P3369 普通平衡树
Luogu P3391 文艺平衡树(Splay)
Luogu P3835 可持久化平衡树
建议试着用FHQ Treap(非旋转Treap)来实现这几题。
你看啊,这个数据结构的常数比Splay小,理解起来比Splay容易,长得比Splay好看,能实现的东西并不比Splay少,代码量比Splay小,还能可持久化,为什么不学学呢?
会FHQ Treap的可以跳过了。
所谓的FHQ Treap其实是一种加强版的Treap。与一般的Treap树不同,FHQ Treap不依赖旋转操作保持自身结构的平衡,而是依赖分裂和合并操作维持树的平衡性质。
我们先来介绍一下关键操作:
1.创建新的节点(new_node):
很简单,就是创建一个新的点,没什么好说的。
返回当前点的下标。
inline int new_node(long long v=0)
{
static int tot(0);
tpi.val=v;tp.sum=v;
tp.rand=rand();tp.size=1;
return tot;
}
2.复制节点(copy_node):
也没什么好说的,仅仅是为了方便。
返回复制后的点的下标。
inline int copy_node(int p)
{
int ret=new_node();
tree[ret]=tree[p];
return ret;
}
3.更新(push_up):
push_up§代表更新下标为p的节点。
inline void push_up(int p)
{
tree[p].size=tls(p).size+trs(p).size+1;
tree[p].sum=tls(p).sum+trs(p).sum+t(p).val;
}
4.标记下传(push_down):
push_down§代表将下标为p的点的标记下传。
什么标记呢?自然是翻转标记。
注意:传之前的点别扔了,留着可持久化呢。
inline void push_down(int p)
{
if(!t(p).tag)return;
if(ls(p))ls(p)=copy_node(ls(p));
if(rs(p))rs(p)=copy_node(rs(p));
swap(ls(p),rs(p));
if(ls(p))tls(p).tag^=1;
if(rs(p))trs(p).tag^=1;
tree[p].tag=0;
}
5.分裂(Split):
这个词我经常打成Spilt。
所谓的"分裂",就是将一颗Treap分成两部分。
你可以理解成,你拿着一个选择性透过膜来"过滤"一颗Treap的过程,最后会将一颗Treap过滤成两个部分。
我们定义split(p,k,x,y)代表将根为p的子树分为两部分,其中的一部分size为k。
具体实现起来就是左子树的size还够用的时候,就往左子树递归,不够用的话就往右子树递归。
先推标记,再分裂!!!
Split操作完整代码:
void split(int p,int k,int &x,int &y)
{
if(!p){x=y=0;return;}
push_down(p);
if(tls(p).size<k){x=copy_node(p);split(rs(x),k-tls(p).size-1,rs(x),y);push_up(x);}
else{y=copy_node(p);split(ls(y),k,x,ls(y));push_up(y);}
}
6.合并(Merge):
合并就更好理解了,就是把两棵子树树合并到一个根节点上。
跟一般的平衡树一样,我们需要以它们的键值大小关系决定怎么合并它们。(键值怎么得到?rand()了解一下)
返回值为他们的根节点。
先推标记,再合并!!!
int merge(int x,int y)
{
if(!x||!y)return x|y;
push_down(x);push_down(y);
if(t(x).rand<t(y).rand){rs(x)=merge(rs(x),y);push_up(x);return x;}
else{ls(y)=merge(x,ls(y));push_up(y);return y;}
}
以下是实现一颗可以拿去持久化的FHQ Treap的代码:
const int N(2e5);
int n;ll lastans;
struct node
{
int rand,size,tag;
ll val,sum;
int lson,rson;
}tree[(N<<7)+10];
int rt[N+10];
inline int new_node(long long v=0)
{
static int tot(0);
tpi.val=v;tp.sum=v;
tp.rand=rand();tp.size=1;
return tot;
}
inline int copy_node(int p)
{
int ret=new_node();
tree[ret]=tree[p];
return ret;
}
inline void push_up(int p)
{
tree[p].size=tls(p).size+trs(p).size+1;
tree[p].sum=tls(p).sum+trs(p).sum+t(p).val;
}
inline void push_down(int p)
{
if(!t(p).tag)return;
if(ls(p))ls(p)=copy_node(ls(p));
if(rs(p))rs(p)=copy_node(rs(p));
swap(ls(p),rs(p));
if(ls(p))tls(p).tag^=1;
if(rs(p))trs(p).tag^=1;
tree[p].tag=0;
}
void split(int p,int k,int &x,int &y)
{
if(!p){x=y=0;return;}
push_down(p);
if(tls(p).size<k){x=copy_node(p);split(rs(x),k-tls(p).size-1,rs(x),y);push_up(x);}
else{y=copy_node(p);split(ls(y),k,x,ls(y));push_up(y);}
}
int merge(int x,int y)
{
if(!x||!y)return x|y;
push_down(x);push_down(y);
if(t(x).rand<t(y).rand){rs(x)=merge(rs(x),y);push_up(x);return x;}
else{ls(y)=merge(x,ls(y));push_up(y);return y;}
}
本题中,我们一共要实现4个操作(单点插入,单点删除,区间反转,区间求和)。
暂且抛开可持久化不谈,具体实现起来也不难。
1.插入:
在第p个数后插入数x,就是把p拆下来然后再使用两遍merge,将它们粘在一起。
插入操作代码:
if(op==1)
{
scanf("%lld%lld",&a,&b);
a^=lastans;b^=lastans;
split(rt[v],a,x,y);
rt[++cnt]=merge(merge(x,new_node(b)),y);
}
2.删除:
删掉第p个数,就是将它的两头分别拆下来,再拼接在一起。
删除操作代码:
if(op==2)
{
scanf("%lld",&a);
a^=lastans;
split(rt[v],a,x,z);
split(x,a-1,x,y);
rt[++cnt]=merge(x,z);
}
3.翻转:
将区间[l,r]翻转,就是将要反转的区间给拆下来,打上标记,再粘回去。
if(op==3)
{
scanf("%lld%lld",&a,&b);
a^=lastans;b^=lastans;
split(rt[v],b,x,z);
split(x,a-1,x,y);
t(y).tag^=1;
rt[++cnt]=merge(merge(x,y),z);
}
4.查询:
查询区间[l,r]的最大值,就是将该区间拆下来,输出树根,再粘回去。
查询操作代码:
if(op==4)
{
scanf("%lld%lld",&a,&b);
a^=lastans;b^=lastans;
split(rt[v],b,x,z);
split(x,a-1,x,y);
printf("%lld\n",lastans=t(y).sum);
rt[++cnt]=merge(merge(x,y),z);
}
代码贴一下:
scanf("%d%d",&v,&op);
if(op==1)
{
scanf("%lld%lld",&a,&b);
a^=lastans;b^=lastans;
split(rt[v],a,x,y);
rt[++cnt]=merge(merge(x,new_node(b)),y);
}
if(op==2)
{
scanf("%lld",&a);
a^=lastans;
split(rt[v],a,x,z);
split(x,a-1,x,y);
rt[++cnt]=merge(x,z);
}
if(op==3)
{
scanf("%lld%lld",&a,&b);
a^=lastans;b^=lastans;
split(rt[v],b,x,z);
split(x,a-1,x,y);
t(y).tag^=1;
rt[++cnt]=merge(merge(x,y),z);
}
if(op==4)
{
scanf("%lld%lld",&a,&b);
a^=lastans;b^=lastans;
split(rt[v],b,x,z);
split(x,a-1,x,y);
printf("%lld\n",lastans=t(y).sum);
rt[++cnt]=merge(merge(x,y),z);
}
为什么FHQ Treap可以依靠可持久化来优化空间复杂度呢?
其实很简单,就是因为Split过程中可以对点进行复制,并且每次修改的必然只有一个子树上的点。
而且Split和Merge总是成对出现,我们就只用复制一次。
完整代码:
#include其实这里就是本总结理论上结束的点,但是我还是整理了其他几个平衡树(虽然不太常用)
所谓的"替罪羊树",指的是重量平衡树。
与一般的平衡树不同,替罪羊树是一颗"暴力"平衡树。
怎么讲呢?
替罪羊树并不依靠平衡化旋转来维持自身的平衡,而是当某颗子树的结构不满足所预设的平衡条件时,就立刻将整棵子树拆成区间再重建。
<插播>
其实替罪羊树这种重建方法一次只对一棵子树造成影响。
所以是可以可持久化的。
什么是替罪羊树的平衡条件呢?
这还真是个学问,因为替罪羊树重构子树p需要O(log(p.size))的时间复杂度(将一个点splay到根上去也才O(logn)),不能够太过频繁地进行重构,容易超时。
这就引出了"重量"平衡树的由来:
替罪羊树平衡条件:
设需判断的点为p,
规定当max(ls(p).size,rs(p).size)>p.size*α时
以p为根的子树是不平衡的。
其中α是一个满足α∈(0.5,1)的定值(常量)。
真是妙不可言。
下面来介绍一下替罪羊树的"拍扁重建"操作。
拍扁重建要3个函数:
将子树拍扁为有序序列的travel函数:
void travel(int p,vector<int>& x)
{
if(!p)return;
travel(ls(p),x);
if(cnt(p))x.push_back(p);
else bc[bc_top++]=p;
travel(rs(p),x);
}
将有序序列建成平衡的BST(二分建树)的devide函数:
int divide(vector<int>& x,int l,int r)
{
if(l>=r)return 0;
int mid=(l+r)>>1;
int p=x[mid];
ls(p)=divide(x,l,mid);
rs(p)=divide(x,mid+1,r);
push_up(p);
return p;
}
拿来调用的rebuild函数:
void rebuild(int& p)
{
static vector<int> v;
v.clear();
travel(p,v);
p=divide(v,0,v.size());
}
图示:
例题:
Luogu P3369 【模板】普通平衡树
代码:
#include