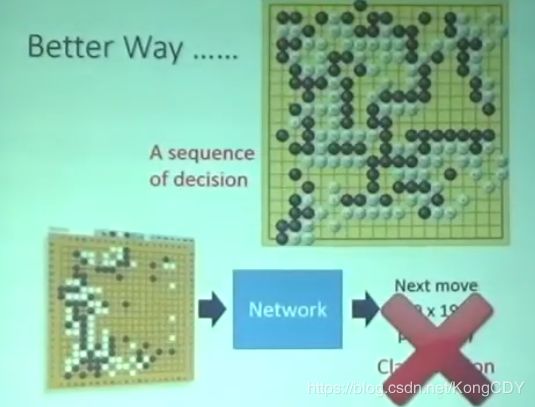
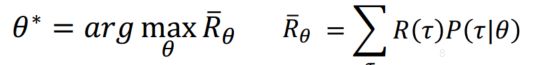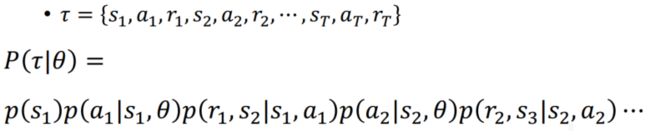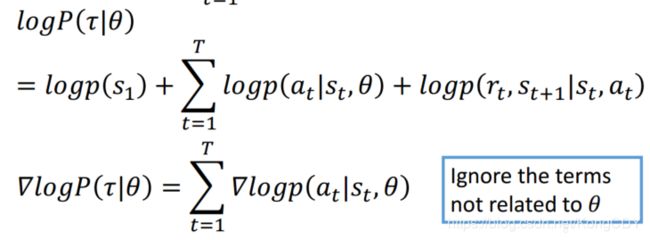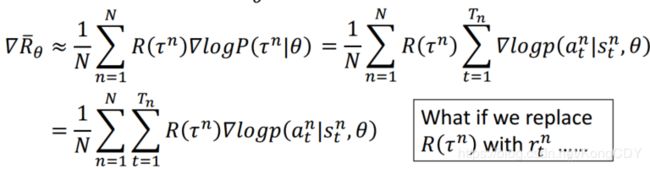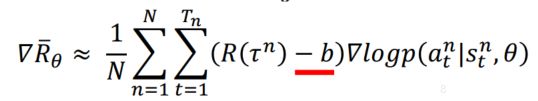强化学习介绍，Policy-Gradient（包含PPO中的部分），李宏毅课程笔记（整合了Lec4的Q-Learning及Imitation Learning）
老师的PPT下载。
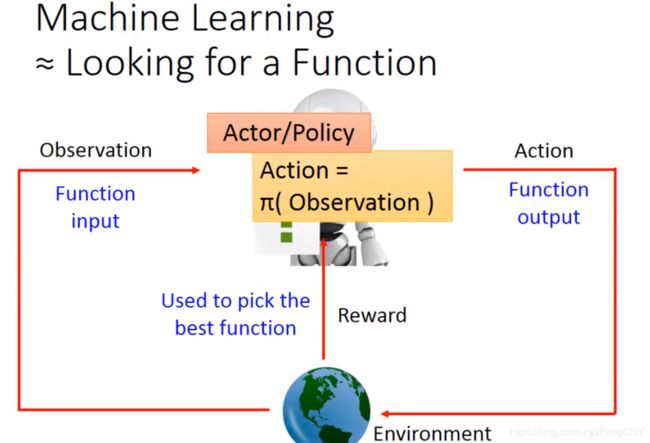
RL 与一般机器学习不同的地方：当前的动作会影响到未来。影响环境、影响接下来看到的东西。
observation与State：observation是更raw的场景或图像，更原始。State是经过处理、去掉冗余后的observation。当模型能力很强的时候，例如一些游戏直接输入画面，那么observation与State就一样了。
仅仅只将与环境的互动问题当做一种supervised问题是学不好的，因为机器不考虑后面的影响，只通过当前的输入做一个决定，无法知道学习到的东西哪些是好的哪些是坏的。
目标：最大化总的reward。难点就是reward跟Env并不是某个网络或某种可导的函数，没法反向求导顺回去调整actor。Env跟Reward往往比较复杂或是个黑盒子，遇到这种情况，就是用policy gradient。
强化学习的难点：
- Reward可能很稀疏，很少能得到正的reward。如何去挖掘正确的action。
- reward delay，往往出现比较晚。然而其他没有得到reward的action也是有用的，可以规划未来，影响未来。
- 探索更多可能，没有做过的行为。
Policy-based
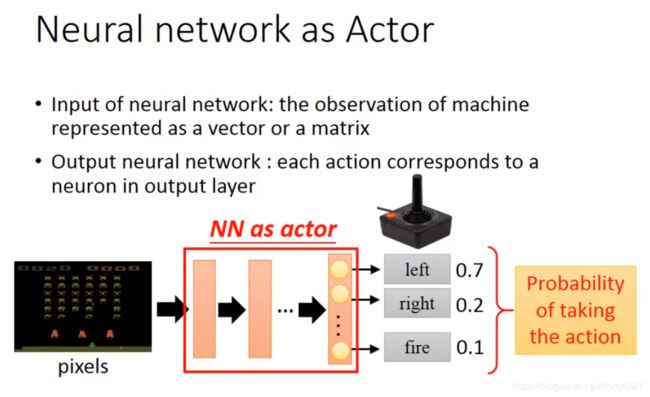
actor是function π，输入observation，输出action。policy即action。
最大化整个episode的reward和。最大化R的期望
。
相当于是用参数为
的actor以概率
采样。玩N次就是以采样N次得到N个。所以上面的红框是可以近似的。目标是：
需要对
求导。
跟没关系，不需要对他求导。此为环境给的反馈，不需要知道是什么样。上面等式右边为了让出现，然后：
按log的微分把上面等式变换成对
的微分，上面的红色框框可以换成采样多个，按上面的近似相加取平均：
之后要计算
：
前面第一项
是
也就是第一个画面出现的几率。第二项
是在状态下采取
的几率，这个与actor有关。第三项
是在状态下采取，跳到
得到
的几率，这个与环境有关。后面以此类推，可以写成：
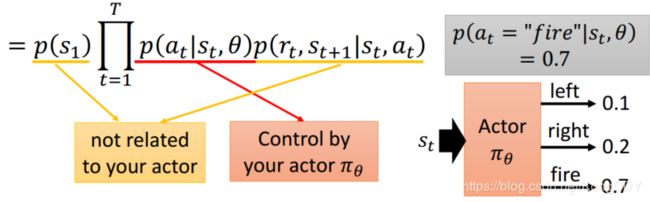
其中黄色底线部分与actor是无关的，只有红色部分有关。然后取log，将相乘变成相加，并去掉与无关的项：
因此
就可以写成，下面一行是把
乘到里面：
这个式子理解成，在
状态下采取
的概率的梯度，并乘以整个这次游戏所得到的reward值。在
这次游戏中，在状态下采取，如果整个游戏得到了正的reward，那就应该调整，使得出现这个动作的概率提高。反之亦然。需要注意的是，这里的
是某时刻
所采取的动作的概率，但是要乘以整个游戏的reward 。假设将换成
的话，那么可能只有fire动作有reward（小蜜蜂游戏），其他动作没有reward，导致模型不会提高其他动作的概率，只提高fire的概率。那么最后actor就只会开火，不会别的了。
为什么要取log？
取log等于右边梯度除以概率。假设不除以概率，因为是所有情况梯度的均值，假设某次游戏的R很高，但是出现的几率很罕见，对总的R影响很小。其他R=1的情况出现的很多，那么均值会前向R=1时的情况，提高R=1时的动作概率亦然可以提高总的R，就使得很罕见的R=2情况下的a动作概率无法提高。那么除以相当于做了一个normalize，将概率比较高的动作b除以一个大值，进行一个平滑。使得优化时不会偏好出现几率高的action。
这里还有个问题就是，假设R都是正的，那么被采样到的action会增加，R大的增加的多，R少的增加的小，也可能会降低，因为最后softmax要将所有动作概率相加为1。那么假设有些action没有被采样到，那么这个action的动作就会被降低。
其解决方案就是在R上减一个bias，这个bias是要自己设定的。相当于有一个baseline，只有R超过了baseline才会提高此R的action，小于baseline的就会减少，这样就不会降低没有被采样到的action的概率了。baseline可以等于reward的均值。
这个公式仍然存在一个问题就是，每对(，)前面乘的是整个episode的权重，换句话说就是整个episode里的(，)都是一个权重，这显然是不公平的。因为整个episode里有些动作是好的有正的reward，有的是不好的reward，但却给他们乘了相同的权重。例如下面的例子，左边episode的reward是+3，但主要来源于第一个action，后面的
、
反而会导致扣分。理想情况下，假设sample够多，这个问题可以被解决。但一般是不够多的，所以需要把这个action的贡献反应出来。其方法就是将此action时刻的reward到最后的reward加起来，作为此数据的权重。因为action之前的reward与这个action无关。此action的行为影响之后的reward。
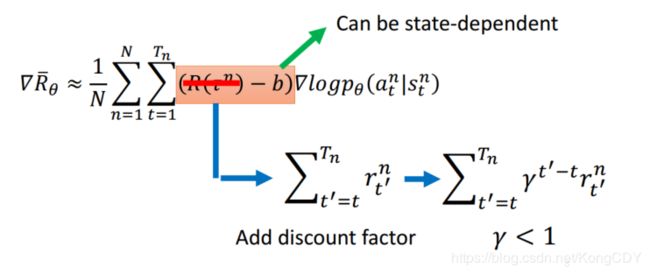
更进一步，对未来的reward做一个discont，衰减。因为当前的动作对更久之后的reward的影响会变小。另外，b可以是与具体state相关的，通常是一个网络输出的。
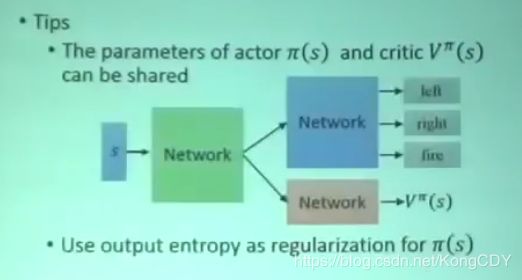
上面的新的R的计算，可以改成下面的advantage function。其衡量在某个state下，采取这个at相对于其他action有多好，是个相对，不是绝对的。这个A通常也可以是一个网络，以后老师讲actor-critic时会讲。万物皆可network……
Policy Gradient
算法步骤：
- 首先随机初始化模型参数θ，准备好测试环境。
- 使用此模型在环境中玩N次，得到N个，把数据收集起来。
- 使用右边公式对R求导，更新。然后返回第一步，如此循环。
前面的公式已经推过了，问题是最后一项
的求导。看下图回想下在分类任务中，优化的是一个cross entroy loss，下图minimize的目标函数。因为一般分类任务的标签是one-hot的，所以就是最大化
，
对应标签所在的类别
。那么相当于最大化 logP("left" | s)，目标的梯度更新即为最底下那行。所以对比上面我们要求的导数，相当于就是优化一个标签为a那个动作类别的cross entroy loss，权重为R。
下图即类比于分类任务，先部分R那部分，被遮住了。因此，相当于输入是s，target是a的分类问题。但是a本身就是输入s所得到的类别，那么网络不是跟没学习一样吗？所以前面要乘以，赋予每个data的一个权重。
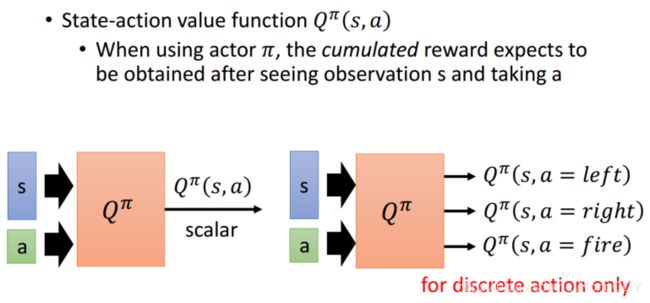
Critic
critic是衡量某个actor 
在某个action时，最终得到的Reward的期望值大小。其结果会随着actor的不同而不同。
例如：以前的光在这里下大马步飞，那critic衡量出bad。后来光变强了，在此时下大马步飞，critic就会比较好。这里光是actor，大马步飞是action，佐为是Critic。
如何估计Critic：
- 基于蒙特卡洛方法，用一个critic去监视actor 玩游戏，当看到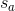
出现时，直到游戏结束所得到的累计Reward 
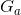。critic就要拟合输入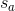输出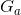，是个回归问题。
- TD方法，
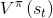求的是
时刻的到最后的累计reward，
求得是t+1时刻到最后的reward，他们之间差值即为
。网络学习的就是这个差值。此方法的好处是不需要等整个episode完事就可以让网络学习。
另一种Critic，Q-learning
输入有action，但一般将不同action的累计reward作为输出。
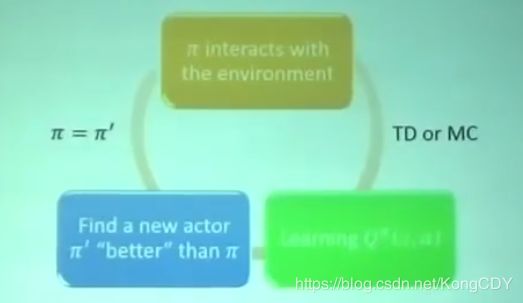
可以用Qfunction找出一个比较好的actor，即Q-learning。初始化一个actor ，通过它与环境互动获得反馈，然后利用TD或MC去学习Q function，利用Q找到一个更好的actor 
，用替换。
对于所有的s，
，即比好。如何找到更好的，当某个状态s下，取的
所有动作对应的最大Q值，作为
的输出，让等于这个更好的值。
DQN的各种trick：Rainbow，整合了6种DQN的改进。
Actor+Critic, A3C
之前是根据reward function的输出来让actor学习如何采取action，得到更好的reward，但是actor与环境的互动会有很多随机性，直接根据随机性的互动可能没法学得很好。A3C的精神是，actor不要跟环境学，不看环境的reward，因为环境的reward随机性大，跟critic学。前两个A，A2C：
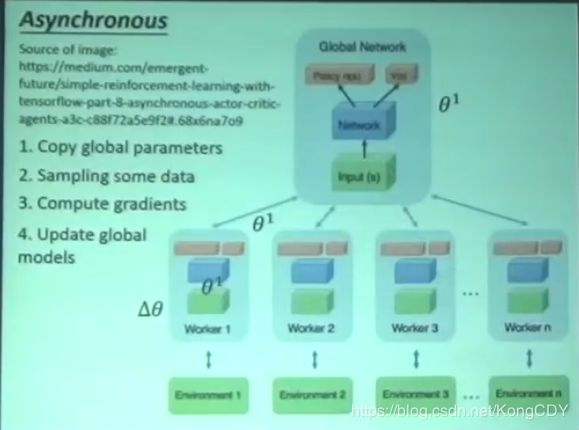
A3C的最后一个A：Asynchronous。有一个全局的actor-critic，将其参数复制N份，其N个分身与环境互动，用上面A2C去学习，然后将所有参数传回去更新全局actor-critic。
下面这个方法是针对连续a的情况，再使用一个actor去输出a，这个a可以使得Q最大。有点类似GAN，Q是D。
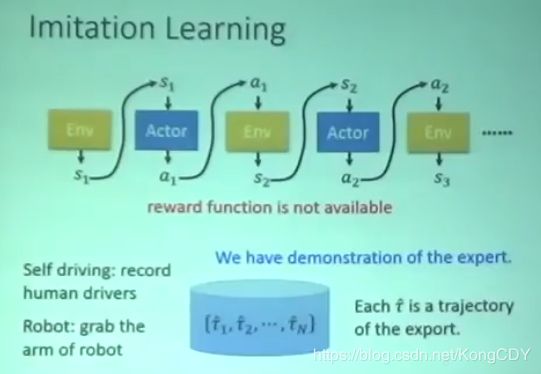
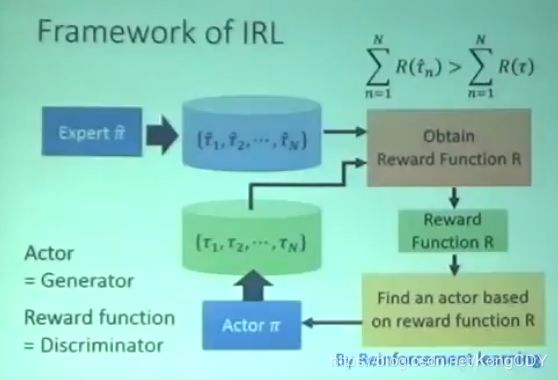
Inverse Reinforcement Learning，Imitation Learning
模仿学习里只有Env跟Actor，没有reward。但是有专家级别的trajectory。
为什么会有模仿学习，因为在现实生活中，reward可能很难定义，不同于游戏。例如自动驾驶、对话机器人。人工设计的reward可能引起actor不确定的行为。
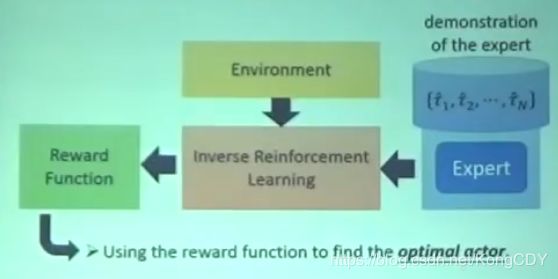
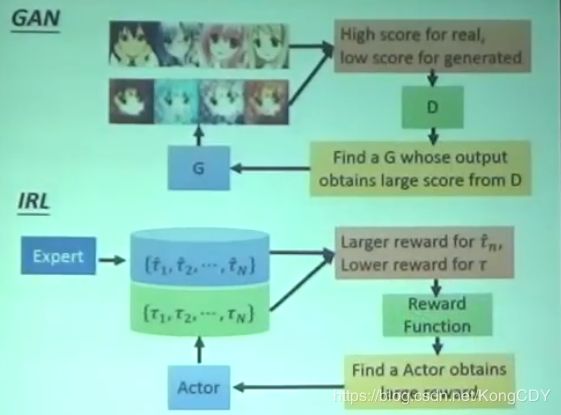
大体流程是：先初始化一个actor。然后让actor与环境互动，得到很多trajectories。然后定义一个reward函数，使其专家得到的trajectories一定比actor得到的好。然后利用新的reward函数去更新actor。如此反复，最后得到reward函数跟actor。整个流程跟GAN很像。
与GAN的比较
