卷积神经网络 + 机器视觉: L4_反向传播_神经网络内部构造 (斯坦福CS231n)
完整的视频课堂链接如下:
- https://www.youtube.com/watch?v=d14TUNcbn1k&index=4&list=PL3FW7Lu3i5JvHM8ljYj-zLfQRF3EO8sYv
完整的视频课堂投影片连接:
- http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf
前一課堂筆記連結:
- 卷积神经网络 + 机器视觉: L3_Loss Functions and Optimization (斯坦福课堂)
反向传播 Backpropagation Function
对于我们人类来说,一个微分的过程无非就是 1. 次方项下移乘以原函数,并且同时次方项数字 -1,但是对于计算机来说这个动作他就不好做了,并且面对一系列样貌不同的方程式,实在是无法用这种人类的思维去设计代码,因此 “反向传播” 的方式因应而生,它把每个方程式细化到一次只有 “一个运算子搭配两个变量” 的计算关系,把不论再复杂的方程式都简化到只用同一个微分规则就可以涵盖的范围,并且算的过程中使用 “chain rule” ,把上个环节的结果传递到下个环节去,于是用代码实现这个统一的微分规则后,就可以套用在任何的复杂算式内,让计算机做重复的动作了。
整个反向传播的发生与肌理是从 “尾” 说起的,下面这张图可以清楚的描述反向传播在每个细分环节的计算目的与手段,每次在一个细分环节要做的事情就是 “专注当下” + “经验总结”。
首先专注当下:
!! 该环节只对 “该对应的运算子搭配两个变量的计算关系” 所得到的结果做微分。
第二经验总结:
!! 当下微分得到的结果,与前面传过来的最新一个历史结果乘在一起做出一个总结。
After knowing two principle above, 不断重复上面两个步骤,直到(天荒地老)整个算式的每一个细节运算子都已经被涵盖,过程就算完结。
下面实战练习一个套入了复杂的 Sigmoid function 后的公式,是如何使用 Backpropagation 的技巧去一层一层剥离复杂的外表,最终算出结果,如下图: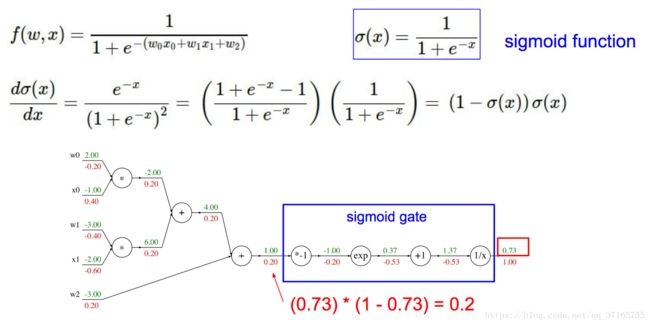
计算过程永远贯彻从 “尾”说起的特性:
1. 把整个公式作为一个整体对着个整体微分,如df/df,结果肯定是 1
2. 令 f(x) = 1/x,df/dx = -1/(x^2),而当下的 x = 1.37 -> -1/(1.37^2) = -0.53,当下专注完了后做总结:-0.53 * 1 = -0.53。
3. 令 f(x) = x + c,df/dx = 1,当下的 0.37 无用武之地,因此直接总结:1 * (-0.53) = -0.53。
4. 令 f(x) = exp(x),df/dx = exp(x),当下的 x = -1.0 -> exp(-1) = 0.368,总结:0.368 * (-0.53)= -0.195。
5. 令 f(x) = cx,df/dx = c,当下的 x = 1 无处使,c = -1 -> 总结:-1 * (-0.195) = 0.195。
6. 来到了 “+” 的分水岭,令 f(x) = x + y,df/dx = 1,df/dy = 1,所以他们当下的 x 或是 y 值都无用,直接总结:1 * 0.2 = 0.2。适用两个节点的值。
7. 同理 6. 结果还都是 0.2。
8. 来到了 “*” 的分水岭,令 f(x) = cx,df/dx = c,c 的值取决于谁与谁相承的那个谁(嗯!)所以就是对家的值,加上总结:-1 * 0.2 = -0.2;2 * 0.2 = 0.4。
9. 同上 8. 的过程,因此直接总结:-3 * 0.2 = -0.6;-2 * 0.2 = -0.4。
最后我们可以用人工的算法直接把算式微分,微分后代入参数验证:(1 - 0.73) * 0.73 = 0.197,得到了一致的结果,因此我们如果喜欢,可以直接把这一大串包成一个 “黑箱” 让我们表面上更易于了解。
而矩阵的反向传播方法与上面详细计算的方法基本上是一样的,照样造句就可以喽。
Cross Validation, the better way to test a model
把数据集 D 划分成 k 个大小相似的互斥子集,每次训练的时候留一个小子集作为测试用途,其他的部分拿去建模,然后重复做 k 次,并把结果与每次留下来的测试集做对比,最后把对比结果取平均,这个方法就称作 “k 折交叉验证” (k-fold cross validation)。
但是这个方法的稳定性和保真性是高度依赖于我们如何切分这些子集的手法,并且一旦达到大规模的数据运算的时候,这个方式非常的消耗运算资源,必须在方法上取得中庸点。
自助法 Bootstrapping
基于数据集 D 随机挑选里面的元素凑合到一个新的 D‘ 数据集里面,D 的元素有几个就重复几次,就像自助餐一样菜品随便挑,并且不在乎是否已经重复被挑选,菜品挑的时候是闭着眼睛选的,几率上算出来会有 36.8% 的元素不会被挑中,剩下的步骤类似于 Cross Validation 一样的手法,这样筛选数据的测试结果又称作 “包外估计” (out-of-bag estimation)。
它比较好的面对数据量比较小的分析,或是那些比较难有效剥离出训练集与测试集的 dataset。But bootstrapping generates the new dataset changing the distribution of the original generation, which might cause some estimation bias.
This is the inspiration coming from the way how a real natural cell works. We receive an input from the external world and react with some combining functions, and finally generate an output as the result.
When we talk about the neural network on a machine,
the input is: the dataset came from the collecting work
the reaction is: the activation function for a judgement
the output is: the result of the activation function, being the next input layer again.
In practice, neural scientists conclude that the non-linearity function ReLU is the model best fit the reality like a living cell.
The characteristics of true biological neurons:
o Many different types
o Dendrites can perform complex non-linear computations
o Synapses are not a single weight but a complex non-linear dynamical system
o Rate code may not be adequate
然而事实上,真实的大脑不是我们想象中的那么简单的过程,全部都是非线性的决策手段加上许多我们尚未知道的动态机制。人工的神经网络架构在电脑里的话,长下面的样子:
这个部分后面单元会细说,搭配 “因地制宜” 的激励函数 activation function,就可以顺利有效的把结果传递到下一层神经网络中去做计算,最后得出一个 “什么是什么” 的分类结果。如果把这张图代码化... 长得下面样子:
class Neuron():
# something functional elements here...
def neuron_tick(inputs):
# assume that inputs and weights are 1 dimensional numpy array and bias is a number
cell_body_sum = np.sum(input * self.weights) + self.bias
firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # this is Sigmoid activation function
return firing_rate
我们可以有效的运用这个方法很快的计算出单一个 neuron 得出来的结果,并传送到下一层去继续运算。
下节链接:卷积神经网络 + 机器视觉: L5_卷积层_Pooling Mechanism (斯坦福课堂)
