C语言和MATLAB分别实现FFT计算并对比

FFT(FastFourierTransform，快速傅里叶变换)算法是离散傅里叶变换的快速算法，FFT算法可以分为按时间抽取和按频率抽取，通过FFT可以将一个信号从时域变换到频域。  

一、FFT和IFFT的C语言编程

（1）对于快速傅里叶变换FFT，第一个要解决的问题就是码位倒序。

码位倒序首先要解决两个问题：a、将t位二进制数倒序     b、将倒序后的两个存储单元进行交换

如果输入序列的自然顺序号i用二进制数表示，例如最大序号为7，即用3位就可表示n2n1n0，则其倒序后j对应的二进制数就是n0n1n2，然后利用C语言的移位功能实现倒序。

（2）第二个要解决的问题就是蝶形运算

a、第1级(第1列)每个蝶形的两节点“距离”为1，第2级每个蝶形的两节点“距离”为2，第3级每个蝶形的两节点“距离”为4，第4级每个蝶形的两节点“距离”为8。由此推得，第m级蝶形运算，每个蝶形的两节点“距离”L=2m-1。
　　   b、对于16点的FFT，第1级有16组蝶形，每组有1个蝶形;第2级有4组蝶形，每组有2个蝶形;第3级有2组蝶形，每组有4个蝶形;第4级有1组蝶形，每组有8个蝶形。由此可推出，对于N点的FFT，第m级有N/2L组蝶形，每组有L=2m-1个蝶形。

 c、旋转因子的确定

以16点FFT为例，第m级第k个旋转因子为，其中k=0～2m-1-1，即第m级共有2m-1个旋转因子，根据旋转因子的可约性，，所以第m级第k个旋转因子为，其中k=0～2m-1-1。

（3）算法实现

N点FFT从左到右共有log2N级蝶形，每级有N/2L组，每组有L个。所以FFT的C语言编程只需用3层循环即可实现：最外层循环完成每一级的蝶形运算(整个FFT共log2N级)，中间层循环完成每一组的蝶形运算(每一级有N/2L组)，最内层循环完成单独1个蝶形运算(每一组有L个)。

  #include    
  #include    
  #include    
  #define   N   1000 
  typedef   struct 
  { 
  double   real; 
  double   img; 
  }complex; 
  void   fft();  
  void   ifft();    void   initW(); /* 初始化变化核 */  
  void   change();  
  void add(complex ,complex ,complex *); /*复数加法*/
  void mul(complex ,complex ,complex *); /*复数乘法*/
  void sub(complex ,complex ,complex *); /*复数减法*/
  void divi(complex ,complex ,complex *);/*复数除法*/  
  void   output();  /*输出结果*/
  complex   x[N],   *W;/* 输出序列的值 */   
  int   size_x=0;/* 输入序列的长度，只限 2的N次方 */   
  double   PI; 
  int   main() 
  { 
  int   i,method; 
  system("cls");   PI=atan(1)*4;/*pi 等于4乘以 1.0 的正切值 */ 
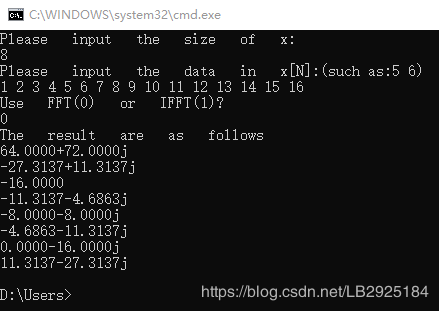
  printf("Please   input   the   size   of   x:\n");   /* 输入序列的长度 */   scanf("%d",&size_x); 
  printf("Please   input   the   data   in   x[N]:(such as:5 6)\n");   /* 输入序列对应的值 */   for(i=0;i0   )    
  {    
  j=j<<1;    
  j|=(k   &   1);    
  k=k>>1;    
  }    
  if(j>i)    
  {    
  temp=x[i];    
  x[i]=x[j];    
  x[j]=temp;    
  }    
  }    
  }    
  void   output()   /* 输出结果 */   {    
  int   i;    
  printf("The   result   are   as   follows\n");    
  for(i=0;i=0.0001)    
  printf("+%.4fj\n",x[i].img);    
  else   if(fabs(x[i].img)<0.0001)    
  printf("\n");    
  else      
  printf("%.4fj\n",x[i].img);    
  }    
  }    
  void   add(complex   a,complex   b,complex   *c)    
  {    
  c->real=a.real+b.real;    
  c->img=a.img+b.img;    
  }    
  void   mul(complex   a,complex   b,complex   *c)    
  {    
  c->real=a.real*b.real   -   a.img*b.img;    
  c->img=a.real*b.img   +   a.img*b.real;    
  }    
  void   sub(complex   a,complex   b,complex   *c)    
  {    
  c->real=a.real-b.real;    
  c->img=a.img-b.img;    
  }    
  void   divi(complex   a,complex   b,complex   *c)    
  {    
  c->real=(   a.real*b.real+a.img*b.img   )/(    
b.real*b.real+b.img*b.img);    
  c->img=(   a.img*b.real-a.real*b.img)/(b.real*b.real+b.img*b.img);    
  }  

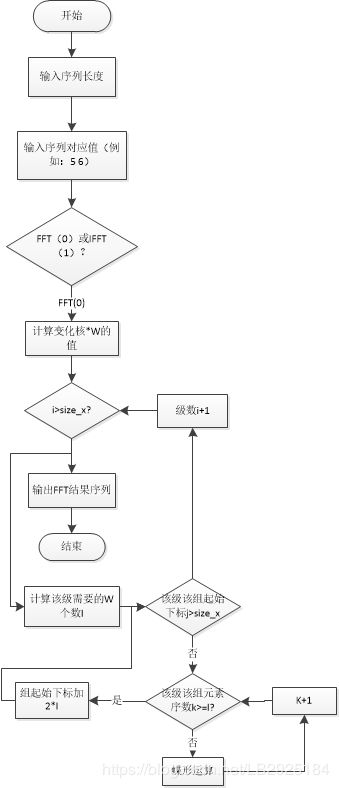
为了更好理解C语言FFT算法的实现，下图是个人根据对代码的理解画的FFT流程图（IFFT的类似就不画了），有不足之处的话请谅解哦。（画流程图建议用微软的VISIO）

二、FFT的Matlab编程

在Matlab中，FFT算法的调用格式是X=fft(x)或者是X=fft(x,N)。对于X=fft(x)，若x的长度是2的整数次幂，则按该长度实现x的快速变换，否则实现的是慢速的非2的整数次幂的变换。对于X=fft(x,N)，N应为2的整数次幂，若x的长度小于N，则补零，若超过N，则舍弃N以后的数据。IFFT的调用格式与之相同。

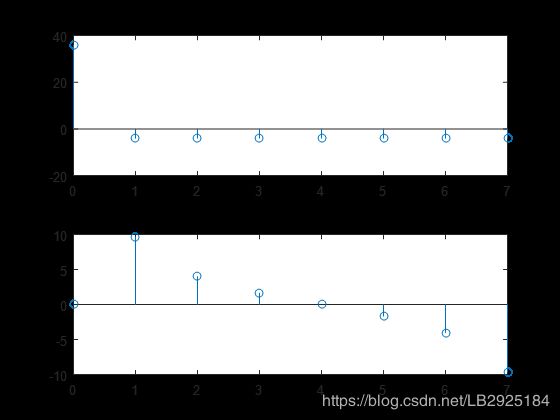
下面就使用X=fft(x,N)函数进行FFT的运算，为了方便分析另外画了FFT计算结果的实部和虚部分布图。

x=input('Please input complex number sequence x[n]='); 
N=input('Please input N='); 
X=fft(x,N); n=0:N-1; 
subplot(211); 
stem(n,real(X)); 
title('Real Part'); 
subplot(212); 
stem(n,imag(X)); 
title('Image Part');

通过对比C语言和Matlab实现的FFT结果发现计算结果存在差异，当然出现问题先别慌，我们再重新看看中间的过程有没有出错的，比如函数和算法对输入序列和长度有没有要求之类的。为了更快找到原因，不妨先把Matlab的fft函数调出来。（命令模式下输入edit fft 即可）。

%FFT Discrete Fourier transform.
%   FFT(X) is the discrete Fourier transform (DFT) of vector X.  For
%   matrices, the FFT operation is applied to each column. For N-D
%   arrays, the FFT operation operates on the first non-singleton
%   dimension.
%
%   FFT(X,N) is the N-point FFT, padded with zeros if X has less
%   than N points and truncated if it has more.
%
%   FFT(X,[],DIM) or FFT(X,N,DIM) applies the FFT operation across the
%   dimension DIM.
%   
%   For length N input vector x, the DFT is a length N vector X,
%   with elements
%                    N
%      X(k) =       sum  x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N.
%                   n=1
%   The inverse DFT (computed by IFFT) is given by
%                    N
%      x(n) = (1/N) sum  X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N.
%                   k=1
%
%   See also FFT2, FFTN, FFTSHIFT, FFTW, IFFT, IFFT2, IFFTN.

%   Copyright 1984-2005 The MathWorks, Inc.

%   Built-in function.

通过观察Matlab内部fft函数可知，对于X=fft(x,N)函数的使用，若x的长度小于N则补零，若超过N则舍弃N以后的数据。我们设定x长度为16，N为8，所以Matlab实际进行FFT的运算时只使用了序列前8个数值，后面的被舍去了，最后造成结果的不一致。

总结：使用Matlab和C语言分别进行FFT的计算，通过对比可以发现一些问题。对于C语言，算法的改进和优化可以减小FFT的运算时间，对于Matlab也可以不使用系统自带函数，通过自己设计算法编程形成.m文件调用，  多学会自己动手编程实现，可以把FFT的理论知识掌握的更加透切。