Polya计数法浅析&caioj1475【Polya计数法】项链上的珠子

Polya计数法
最近学习了一个很高深的算法QAQ，它就是polya计数法那么我们就来学习一下这个算法吧~~~请先看下面这道例题：
【例题】
对2*2的方阵用黑白两种颜色涂色，问能得到多少种不同的图像？经过旋转使之吻合的两种方案，算是同一种方案。
【问题分析】
由于该问题规模很小，我们可以先把所有的涂色方案列举出来。

一个2*2的方阵的旋转方法一共有4种：旋转0度、旋转90度、旋转180度和旋转270度。(注：本文中默认旋转即为顺时针旋转) 我们经过尝试，发现其中互异的一共只有6种：C3、C4、C5、C6是可以通过旋转相互变化而得，算作同一种；C7、C8、C9、C10是同一种；C11、C12是同一种；C13、C14、C15、C16也是同一种； C1和C2是各自独立的两种。于是，我们得到了下列6种不同的方案。

但是，一旦这个问题由2*2的方阵变成20*20甚至200*200的方阵，我们就不能再一一枚举了，利用Polya计数法成了一个很好的解题方法。在接触Polya计数法之前，首先简单介绍Polya计数法中要用到的一些概念。
群：给定一个集合G={a,b,c,…}和集合G上的二元运算，并满足:
（1） 封闭性
若a,b∈G,则存在唯一确定的c∈G,使得a*b=c;
（2） 结合律成立
任意a,b,c∈G,有(a*b)c=a(b*c);
（3） 单位元存在
存在e∈G,对任意a∈G，满足a*e=e*a=a，称e为单位元
（4） 逆元存在
任意a∈G,存在唯一确定的b∈G, a*b=b*a=e（单位元），则称a与b互为逆元素，简称逆元，记作a^(-1)=b.
则称集合G在运算＊之下是一个群，简称G是群。一般a＊b简写为ab。
置换：n个元素1,2,…,n之间的一个置换 表示1被1到n中的某个数a1取代，2被1到n中的某个数a2取代，直到n被1到n中的某个数an取代，且a1,a2,…,an互不相同。本例中有4个置换：

转0 度 a1=
转90 度 a2=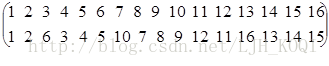
转180 度 a3=
转270 度 a4=
置换群：置换群的元素是置换，运算是置换的连接。例如：

可以验证置换群满足群的四个条件。
本题中置换群G={转0度、转90度、转180度、转270度}
我们再看一个公式：│Ek│•│Zk│=│G│ k=1…n
该公式的一个很重要的研究对象是群的元素个数，有很大的用处。
Zk (K不动置换类)：设G是1…n的置换群。若K是1…n中某个元素，G中使K保持不变的置换的全体，记以Zk，叫做G中使K保持不动的置换类，简称K不动置换类。
如本例中：G是涂色方案1~16的置换群。对于方案1，四个置换都使方案1保持不变，所以Z1={a1, a2, a3, a4}；对于方案3，只有置换a1使其不变，所以Z3={a1}；对于方案11，置换a1和a3使方案其保持不变，所以Z11={a1, a3}。

Ek(等价类)：设G是1…n的置换群。若K是1…n中某个元素，K在G作用下的轨迹，记作Ek。即K在G的作用下所能变化成的所有元素的集合。
如本例中：方案1在四个置换作用下都是方案1，所以E1={1}；方案3，在a1下是3，在a2下变成6，在a3下变成5，在a4下变成4，所以E3={3,4,5,6}；方案11，在a1、a3下是11，在a2、a4下变成12，所以E11={11,12}。
本例中的数据，也完全符合这个定理。如本例中：
│E1│•│Z1│= 1*4 = 4 =│G│
│E3│•│Z3│= 4*1 = 4 =│G│
│E11│•│Z11│= 2*2 = 4 =│G│
限于篇幅，这里就不对这个定理进行证明。
接着就来研究每个元素在各个置换下不变的次数的总和。见下表：

其中

D(aj) 表示在置换aj下不变的元素的个数
如本题中：涂色方案1在a1下没变动，S1,1=1；方案3在a3变动了， S3,3=0；在置换a1的变化下16种方案都没变动，D(a1)=16；在置换a2下只有1、2这两种方案没变动，D(a2)=2。
一般情况下，我们也可以得出这样的结论：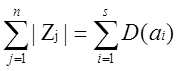

我们对左式进行研究。
不妨设N={1，……，n}中共有L个等价类，N=E1+ E2+……+EL，则当j和k属于同一等价类时，有│Zj│=│Zk│。所以

这里的L就是我们要求的互异的组合状态的个数。于是我们得出：

利用这个式子我们可以得到本题的解 L=(16+2+4+2)/4=6 与前面枚举得到的结果相吻合。这个式子叫做Burnside引理。

但是，我们发现要计算D(aj)的值不是很容易，如果采用搜索的方法，总的时间规模为O(n*s*p)。(n表示元素个数，s表示置换个数，p表示格子数，这里n的规模是很大的) 下一步就是要找到一种简便的D(aj)的计算方法。先介绍一个循环的概念：
循环：记

称为n阶循环。每个置换都可以写若干互不相交的循环的乘积，两个循环(a1a2…an)和(b1b2…bn)互不相交是指aibj, i,j=1,2,…,n。例如：

这样的表示是唯一的。置换的循环节数是上述表示中循环的个数。例如(13)(25)(4)的循环节数为3。
有了这些基础，就可以做进一步的研究，我们换一个角度来考虑这个问题。我们给2*2方阵的每个方块标号，如下图：
2 1
3 4
　　构造置换群G’={g1,g2,g3,g4},｜G’｜＝4，令gi的循环节数为c(gi) (i=1,2,3,4)
在G’的作用下，其中
g1表示转0° , 即g1=(1)(2)(3)(4) c(g1)=4
g2表示转90°, 即g2=(4 3 2 1) c(g2)=1
g3表示转180°, 即g3=(1 3)(2 4) c(g3)=2
g4表示转270°, 即g4=(1 2 3 4) c(g4)=1
　　我们可以发现，gi的同一个循环节中的对象涂以相同的颜色所得的图像数mc(gi) 正好对应Ｇ中置换ai作用下不变的图象数，即
　　　2^c(g1)=2^4=16=D(a1) 2^c(g2)=2^1=2= D(a2)
　　　2^c(g3)=2^2=4=D(a3) 2^c(g4)=2^1=2= D(a4)
由此我们得出一个结论：
　　设G是p个对象的一个置换群，用m种颜色涂染p个对象，则不同染色方案为：
　　
其中G={g1 ,…gs} c(gi )为置换gi的循环节数(i=1…s)
这就是所谓的Polya计数法。我们发现利用Polya计数法的时间复杂度为O(s*p) (这里s表示置换个数，p表示格子数)，与前面得到的Burnside引理相比之下，又有了很大的改进，其优越性就十分明显了。Polya计数法充分挖掘了研究对象的内在联系，总结了规律，省去了许多不必要的盲目搜索，把解决这类问题的时间规模降到了一个非常低的水平。
既然推出了Polya的公式，我们就一起来看一道题吧！>_<

CAIOJ1475【Polya计数法】项链上的珠子
【题意】
一个圆形项链，上面均匀分布着n颗豆子，要对豆子进行红绿蓝三色的涂色，问可以涂出多少条不同的项链。
注意：按照对称轴的翻转和中心的旋转所生成的项链均认为与原项链相同，不能计数。
【输入格式】
输入一个整数n（n<24），代表有n颗豆子。
当n=-1时停止输入
【输出格式】
输出总的方案数，代表可以涂出多少条不同的项链。
【样例输入】
4
5
-1
【样例输出】
21
39

这道题有两种置换方法，旋转和翻转。

旋转置换，枚举旋转的豆子个数，置换数为n，循环节长度为LCM(i,n)/i，循环节数为n/(LCM(i,n)/i)=gcd(i,n)
翻转置换，假如是奇数，就只有一种情况，n个豆子有n种置换，循环节为(n+1)/2；假如是偶数，两种情况，对称轴过豆子或过间隔：对称轴过间隔，所有豆子翻转，有n/2种置换，循环节为n/2；对称轴过豆子，两个豆子不变，其他翻转，有n/2种置换，循环节为(n+2)/2。
最后我们带入公式，不要忘了还要除以一个|G|，|G|=n+n或n+n/2+n/2=n*2

Code:

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;  
typedef long long LL;  
LL gcd(LL a,LL b)
{
    if(a==0)return b;
    return gcd(b%a,a);
}  
LL pow(LL A,LL k)
{
    LL ans=1;
    while(k!=0)
    {
        if(k%2==1)ans*=A;
        A*=A;k/=2;
    }
    return ans;
}
int main() 
{  
    LL n;
    while(scanf("%lld",&n)!=EOF) 
    {  
        if(n==-1)break;
        if(n==0){printf("0\n");continue;}
        LL ans=0;
        for(int i=1;i<=n;i++)ans+=pow(3,gcd(i,n)); 
        //旋转置换，枚举旋转的豆子个数，置换数为n，循环节长度为LCM(i,n)/i，循环节数为n/(LCM(i,n)/i)=gcd(i,n)
        //翻转置换 
        if(n%2==1)//假如是奇数，就只有一种情况，n个豆子有n种置换，循环节为(n+1)/2
        {
            ans+=n*pow(3,(n+1)/2);
        }
        else//假如是偶数，两种情况，对称轴过豆子或过间隔
        { 
            ans+=n/2*pow(3,n/2);//对称轴过间隔，所有豆子翻转，有n/2种置换，循环节为n/2
            ans+=n/2*pow(3,(n+2)/2);//对称轴过豆子，两个豆子不变，其他翻转，有n/2种置换，循环节为(n+2)/2
        }
        printf("%lld\n",ans/(n*2));//G=n*2
    }
    return 0;  
}  

下面给几道例题做一下~~
CAIOJ1476
CAIOJ1477
CAIOJ1478