技术图文:如何利用C#实现Huffman编码?
背景
Huffman编码 在通信和数据压缩领域具有重要的应用。
在介绍 Huffman 编码具体实现之前,先介绍几个相关的概念。
概念1:树中结点的带权路径长度 – 根结点到该结点的路径长度与该结点权值的乘积。
概念2:树的带权路径长度 – 树中所有叶子结点的带权路径长度之和。
概念3:huffman树 – n个带权叶子结点构成的所有二叉树中,带权路径长度最小的二叉树。
概念4:前缀码规则 – 对字符集编码时,字符集中任一字符的编码都不是其它字符编码的前缀。
概念5:哈夫曼编码 – 将哈夫曼树中,每个分支结点的左分支标0,右分支标1,把从根结点到每个叶子结点的路径上的标号连接起来作为该叶子结点所代表符号的编码,这样得到的编码称为Huffman编码。
huffman编码 是满足前缀码规则的编码方案,对利用 huffman编码 的字符集,进行解码时不存在二义性。
技术分析
要对一个字符集合,例如“state,seat,act,tea,cat,set,a,eat”进行编码。
首先,要对每个字符出现的频数进行统计,根据统计的结果构造 Huffman 树。
- 字符
c,出现的频数为2。 - 字符
s,出现的频数为3。 - 字符
e,出现的频数为5。 - 字符
a,出现的频数为7。 - 字符
,,出现的频数为7。 - 字符
t,出现的频数为8。
构造 Huffman 树的算法如下:
第1步:根据给定的 n 个权值 w1,w2,……,wn,构成 n 棵二叉树的森林 F={T1,T2,……,Tn} ,其中每棵二叉树 Ti 中都只有一个权值为 wi 的根结点,其左右子树均为空(对应代码实现的Step3)。
第2步:在森林 F 中选出两棵根结点权值最小的树作为一棵新树的左右子树,且置新树的根结点的权值为其左右子树上根结点的权值之和。
第3步:从 F 中删除构成新树的哪两棵树,同时把新树加入 F 中。
第4步:重复第2和3步,直到 F 中只含有一棵树为止,此树便是Huffman树(对应代码实现的Step4)。
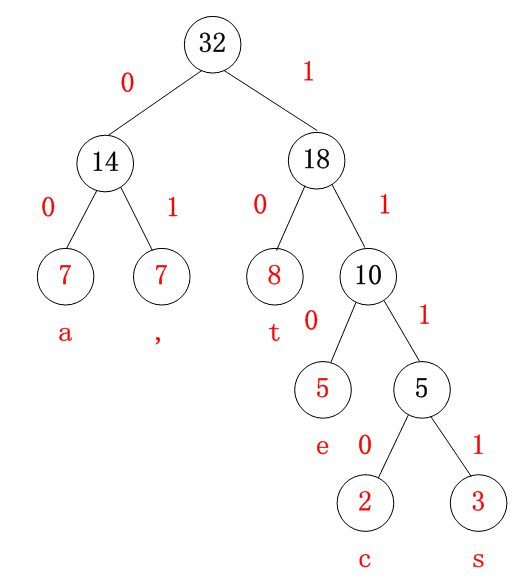
该算法为典型的贪心算法,以上字符集经过处理后得到的 Huffman树,如下所示:
其次,利用 Huffman 树对字符集中的每个字符进行编码,得到字符与编码对应的字典(对应代码实现的Step5)。
- 字符
c,对应的编码1110。 - 字符
s,对应的编码1111。 - 字符
e,对应的编码110。 - 字符
a,对应的编码00。 - 字符
,,对应的编码01。 - 字符
t,对应的编码10。
最后,利用字典对数据进行编码和解码(对应代码实现的Step6、Step7)。
对数据 state,seat,act,tea,cat,set,a,eat 进行编码,得到的结果如下:
1111100010110011111110001001001110100110110000111100010011111110100100011100010
当然,由于 Huffman 编码满足前缀码规则,解码之后仍然为:state,seat,act,tea,cat,set,a,eat,具有唯一性。
代码实现
Step1:构造 Huffman 树结点的结构 HuffmanTreeNode。
封装二叉树结点的结构
public class BinTreeNode<T> : where T : IComparable<T>
{
private T _data;
/// 封装 Huffman 树结点的结构,该结点为二叉树节点的子类。
public class HuffmanTreeNode : BinTreeNode<char>
{
/// Step2:封装编码字典的结构HuffmanDicItem。
public class HuffmanDicItem
{
/// Step3:对字符集中的字符进行统计的函数,即构造最初始的森林F。
private List<HuffmanTreeNode> CreateInitForest(string str)
{
if (string.IsNullOrEmpty(str))
throw new ArgumentNullException();
List<HuffmanTreeNode> result = new List<HuffmanTreeNode>();
char[] charArray = str.ToCharArray();
List<IGrouping<char, char>> lst = charArray.GroupBy(a => a).ToList();
foreach (IGrouping<char, char> g in lst)
{
char data = g.Key;
int weight = g.ToList().Count;
HuffmanTreeNode node = new HuffmanTreeNode(data, weight);
result.Add(node);
}
return result;
}
Step4:构造Huffman树的函数。
private HuffmanTreeNode CreateHuffmanTree(List<HuffmanTreeNode> sources)
{
if (sources == null)
throw new ArgumentNullException();
if (sources.Count < 2)
throw new ArgumentException("构造Huffman树,最少为2个结点。");
HuffmanTreeNode root = default(HuffmanTreeNode);
bool isNext = true;
while (isNext)
{
List<HuffmanTreeNode> lst = sources.OrderBy(a => a.Weight).ToList();
HuffmanTreeNode n1 = lst[0];
HuffmanTreeNode n2 = lst[1];
int weight = n1.Weight + n2.Weight;
HuffmanTreeNode node = new HuffmanTreeNode(weight);
node.LeftChild = n1;
node.RightChild = n2;
if (lst.Count == 2)
{
root = node;
isNext = false;
}
else
{
sources = lst.GetRange(2, lst.Count - 2);
sources.Add(node);
}
}
return root;
}
Step5:构造Huffman编码字典的函数。
private List<HuffmanDicItem> CreateHuffmanDict(string code,
HuffmanTreeNode current)
{
if (current == null)
throw new ArgumentNullException();
List<HuffmanDicItem> result = new List<HuffmanDicItem>();
if (current.LeftChild == null && current.RightChild == null)
{
result.Add(new HuffmanDicItem(current.Data, code));
}
else
{
List<HuffmanDicItem> dictL = CreateHuffmanDict(code + "0",
(HuffmanTreeNode) current.LeftChild);
List<HuffmanDicItem> dictR = CreateHuffmanDict(code + "1",
(HuffmanTreeNode) current.RightChild);
result.AddRange(dictL);
result.AddRange(dictR);
}
return result;
}
private List<HuffmanDicItem> CreateHuffmanDict(HuffmanTreeNode root)
{
if (root == null)
throw new ArgumentNullException();
return CreateHuffmanDict(string.Empty, root);
}
Step6:对字符串进行编码的函数。
private string ToHuffmanCode(string source, List<HuffmanDicItem> lst)
{
if (string.IsNullOrEmpty(source))
throw new ArgumentNullException();
if (lst == null)
throw new ArgumentNullException();
string result = string.Empty;
for (int i = 0; i < source.Length; i++)
{
result += lst.Single(a => a.Character == source[i]).Code;
}
return result;
}
// 被外界调用的函数,对字符串进行huffman编码。
public string StringToHuffmanCode(out List<HuffmanDicItem> dict,
string str)
{
List<HuffmanTreeNode> forest = CreateInitForest(str);
HuffmanTreeNode root = CreateHuffmanTree(forest);
dict = CreateHuffmanDict(root);
string result = ToHuffmanCode(str, dict);
return result;
}
Step7:对编码后的字符串进行解码的函数。
public string HuffmanCodeToString(List<HuffmanDicItem> dict, string code)
{
string result = string.Empty;
for (int i = 0; i < code.Length;)
{
foreach (HuffmanDicItem item in dict)
{
if (code[i] == item.Code[0] && item.Code.Length + i <= code.Length)
{
string temp = code.Substring(i, item.Code.Length);
if (temp == item.Code)
{
result += item.Character;
i += item.Code.Length;
break;
}
}
}
}
return result;
}
总结
我们把 Step3至Step7 的代码封装在HuffmanTree的结构中。通过调用该结构提供的两个 public 方法StringToHuffmanCode和HuffmanCodeToString就可以实现对给定字符集的 huffman 编码与解码的操作。
static void Main(string[] args)
{
string str = "state,seat,act,tea,cat,set,a,eat";
Console.WriteLine(str);
HuffmanTree huffmanTree = new HuffmanTree();
List<HuffmanDicItem> dic;
string code = huffmanTree.StringToHuffmanCode(out dic, str);
for (int i = 0; i < dic.Count; i++)
{
Console.WriteLine(dic[i].Character + ":" + dic[i].Code);
}
Console.WriteLine(code);
string decode = huffmanTree.HuffmanCodeToString(dic, code);
Console.WriteLine(decode);
Console.ReadLine();
}
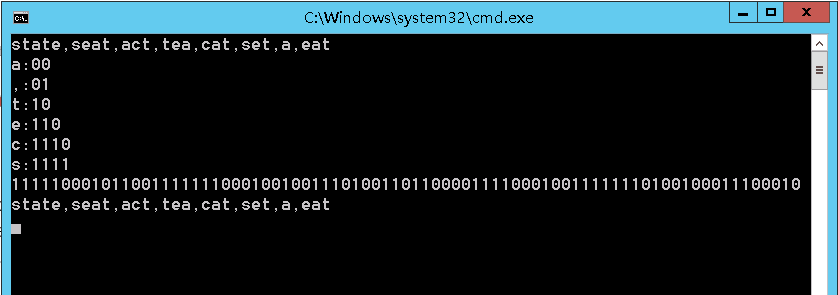
运行的结果如下所示:
好了,有关 Huffman编码就给大家介绍完了,该编码是二叉树的重要应用之一,希望对学习数据结构与算法的同学有所帮助。See You!
相关图文:
- 如何利用 C# 实现 K 最邻近算法?
- 如何利用 C# 实现 K-D Tree 结构?
- 如何利用 C# + KDTree 实现 K 最邻近算法?
- 如何利用 C# 对神经网络模型进行抽象?
- 如何利用 C# 实现神经网络的感知器模型?
- 如何利用 C# 实现 Delta 学习规则?
- 如何利用 C# 开发「桌面版百度翻译」软件!
- 如何利用 C# 开发「股票数据分析软件」(上)
- 如何利用 C# 开发「股票数据分析软件」(中)
- 如何利用 C# 开发「股票数据分析软件」(下)
- 如何利用 C# 爬取「财报说」中的股票数据?
- 如何利用 C# 爬取 One 持有者返利数据!
- 如何利用 C# 爬取Gate.io交易所的公告!
- 如何利用 C# 爬取BigOne交易所的公告!
- 如何利用 C# 爬取 ONE 的交易数据?
- 如何利用 C# 爬取「京东 - 计算机与互联网图书销量榜」!
- 如何利用 C# 爬取「当当 - 计算机与互联网图书销量榜」!
- 如何利用 C# 爬取「互动出版网 - 计算机图书销量榜」!
- 如何利用 C# 爬取「中国图书网 - 计算机与互联网图书销量榜」!
- 如何利用 C# 爬取「猫眼电影:热映口碑榜」及对应影片信息!
- 如何利用 C# 爬取「猫眼电影专业版:票房」数据!
- 如何利用 C# 爬取「猫眼电影:最受期待榜」及对应影片信息!
- 如何利用 C# 爬取「猫眼电影:国内票房榜」及对应影片信息!
- 如何利用 C# + Python 破解猫眼电影的反爬虫机制?
- 如何利用 C# 爬取带 Token 验证的网站数据?
- 如何利用 C# 向 Access 数据库插入大量数据?