MATLAB之绘图基础
第7部分 MATLAB的绘图基础
1.二维图形绘制
(1)plot()函数
格式:
plot(x)
plot(x,y)
图形绘制函数plot(x)的格式说明
| x内容 |
说明 |
| 实向量y |
以y元素下标序号i为横坐标,元素y为纵坐标,绘制(I,y)的有序集合的图形,中间以线段连接 |
| 实矩阵 |
对于矩阵 |
| 负数矩阵 |
对于mXn的复数矩阵,每行以横轴为实轴,纵轴为虚轴,绘制(real( |
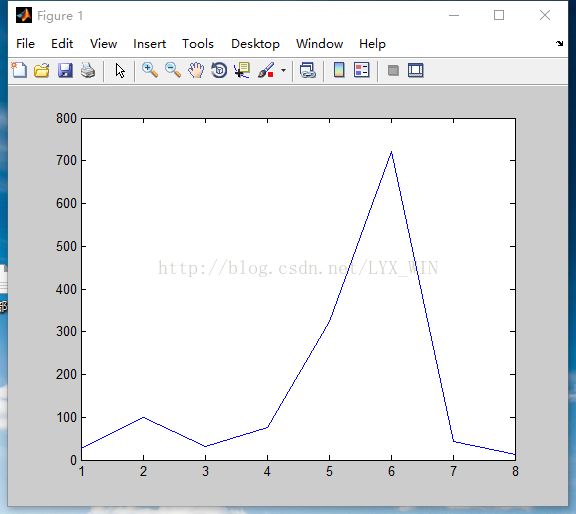
例.利用函数plot()来绘制实向量Y=[27,99,31,75,325,721,43,12]、A=[23,672;440,100;543,64]和复数矩阵Z=[25-23i,63-77i,34-64i,123-34i]
>> Y=[27,99,31,75,325,721,43,12];
>> plot(Y)
>> A=[23,672;440,100;543,64];
>> plot(A)
>> Z=[25-23i,63-77i,34-64i,123-34i];
>> plot(Z)
图形绘制函数plot(X,Y)的格式说明
| X数据类型 |
Y数据类型 |
说明 |
| 实向量x |
与x同长度的实向量y |
绘制以同下标的x为横坐标,y为纵坐标的曲线段 |
| 长度为m或n的实向量x |
维度为mXn的矩阵 |
绘制矩阵A对向量x的图形,对mXn的矩阵A和长度为m的向量x,绘制矩阵A的列对向量x的图形。如果x的长度为n,则绘制矩阵A的行对向量x的图形。向量x可以是行向量也可以是列向量 |
| 维度为mXn的矩阵 |
长度为m或n的实向量x |
对矩阵A绘制向量x的图形,对于一个mXn的矩阵A个长度为m的向量x,对矩阵A的列绘制向量x的图形。如果x的长度为n,则对矩阵A的行绘制向量x的图形。向量x可以是行向量,也可以是列向量 |
| 维度为mXn的矩阵 |
维度为mXn的矩阵 |
对矩阵A的行绘制矩阵的B的列的图形。如果A和B都是mXn的矩阵,将绘制n条由m个有序对连成的曲线 |
(2)线型、标记和颜色
|
颜色 |
符号 |
b |
g |
r |
c |
||||||||||
| 说明 |
蓝色 |
绿色 |
红色 |
青色 |
|||||||||||
| 符号 |
m |
y |
k |
w |
|||||||||||
| 说明 |
品红色 |
黄色 |
黑色 |
白色 |
|||||||||||
| 线性 |
符号 |
- |
: |
-. |
-- |
|
|||||||||
| 说明 |
实线 |
点线 |
画点线 |
虚线 |
无 |
||||||||||
|
标记点型 |
符号 |
. |
o |
x |
* |
+ |
none |
< |
|||||||
| 说明 |
点 |
圈 |
X号 |
星号 |
+ |
无点 |
顶点指定左边的三角 |
||||||||
| 符号 |
S |
d |
p |
h |
^ |
v |
> |
||||||||
| 说明 |
正方形 |
菱形 |
五角星形 |
六角星形 |
正三角 |
倒三角 |
顶点指向右边的三角 |
||||||||
例.利用plot()函数实现图形曲线的线型、颜色和标记点的改变
>> x=-pi:pi/10:pi;
>> y=tan(sin(x))-sin(tan(x));
>> plot(x,y,'--rp')
修饰命令集
| proerty |
说明 |
内容 |
| LineWidh |
曲线线宽 |
数值 |
| MarkerEdgeColor |
标记点边框线条颜色 |
颜色字符 |
| MarkerFaceColor |
标记点填充颜色 |
颜色字符 |
| MarkerSize |
标记点大小 |
数值 |
(3)多个图形叠绘及多个图形窗口
| 表达式 |
说明 |
| hold |
切换当前的绘图叠加模式,将当前的绘图窗口的叠加模式从off切换至on,或者从on切换至off |
| hold on |
当前叠加绘图模式状态为开,即保持当前轴及图形,准备接受绘制的新图形 |
| hold off |
当前叠加绘图模式状态开关,即当前轴及图形不再具有叠加绘图的性质 |
| hold all |
不用实现hold on的功能,使当前的叠加绘图模式打开,而且使新的绘图函数依然循环初始设置的颜色循环顺序和线型循环顺序 |
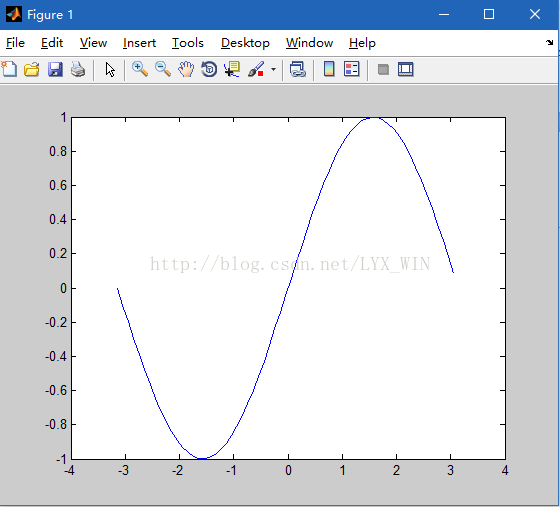
例.利用plot()函数绘制正弦函数sin()的图像,然后进行叠绘状态的转换,并在原图形上进行叠绘操作。
>> x=-pi:0.1:pi;
>> y=sin(x);
>> plot(x,y)
>> hold on
>> Current plot held
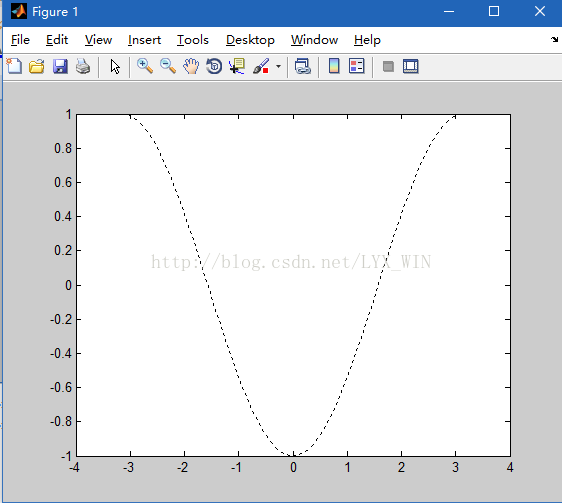
>> z=cos(x);
>> plot(x,z,'--r')
>> hold
Current plot released
>> m=-cos(x);
>> plot(x,m,':k')
(4)子图绘制
subplot(m,n,k):在当前绘图区域建立m行n列绘图子区,并在第k个子区建立坐标系,设置该子区为当前图绘制区域
subplot(‘position’,[left,bottom,widt,hight]):在当前绘图窗口的指定位置开辟子图所需的子区,并在子区建立坐标系,设置该子区为当前图绘制区域。[left,bottom,widt,hight]为实数行矩阵,left的值为距离绘图框左边框的距离值;bottom的值为距离绘图框底部的距离值;width为子图框的宽度值;hight为子图框的高度值。
例.利用suplot()函数在MATLAB绘图窗口创建多子图
>> t=-pi:0.01:pi;
>> y1=sin(t);
>> y2=cos(5*t);
>> y3=sin(4*t).*sin(t);
>> y4=sin(y3).*cos(t);
>> subplot(3,2,1),plot(t,y1)
>> title('子图一');
>> subplot(3,2,2),plot(t,y2)
>> title('子图二');
>> subplot(3,2,3),plot(t,y3)
>> title('子图三');
>> subplot('position',[0.3,0.05,0.6,0.3]),plot(t,y4);
>> title('子图四');
(5)交互式绘图和屏幕刷新
a.ginput()函数
[x,y]=ginput(n):该函数可使用户通过鼠标捕捉所在二维图形坐标系中的n歌点的坐标值,并将其记录下来。若取点不超过n可以通过按【Enter】键来结束;若n缺省则可以取无限个点的坐标值,按【Enter】键结束取点。
[x,y,button]=ginput(n):该函数形式中n的说明同上。button是返回捕捉点按键所代表的数值,如左键为1,中键为2,右键为3.其他键则为其对应的ASCII值,如A键为65,1键为49等。
例.绘制正弦函数sin()的图形,并用ginput()函数的第一种形式来捕捉函数图形的零点和顶点,顺次用鼠标右键,S键和1键来捕捉任意3点的值,并输出bottom值
>> x=-pi:pi/1000:pi;
>> y=sin(x);
>> plot(x,y)
>> [x,y]=ginput(4)
x =
0.4689
0.6555
0.2062
0.2016
y =
0.4956
0.4927
0.0863
-0.0015
>> [x,y,bottom]=ginput()
x =
0.1141
0.2730
y =
0.4459
0.1798
bottom =
1
1
b.zoom()函数
| 命令 |
说明 |
| zoom |
对图形缩放状态进行命令的切换 |
| zoom(factor) |
factor为缩放因子 |
| zoom on |
允许对坐标轴进行缩放 |
| zoom off |
取消对坐标轴的缩放 |
| zoom out |
恢复对坐标值的设置 |
| zoom reset |
将当前的坐标轴设置为初始值 |
| zoom xon |
允许对x轴进行缩放 |
| zoom yon |
允许对y进行缩放 |
(6)使用plotyy()函数绘制双坐标轴
a.叠绘发绘图
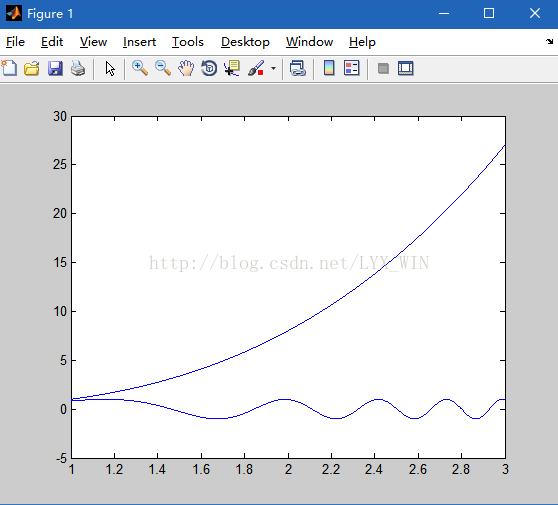
例.利用hold on将两个函数图绘制在一个坐标轴中
>> x=1:0.001:3;
>> y1=x.^3;
>> y2=sin(y1);
>> plot(x,y2)
>> hold on
>> Current plot released
>> plot(x,y1)
b.使用plotyy()函数绘图
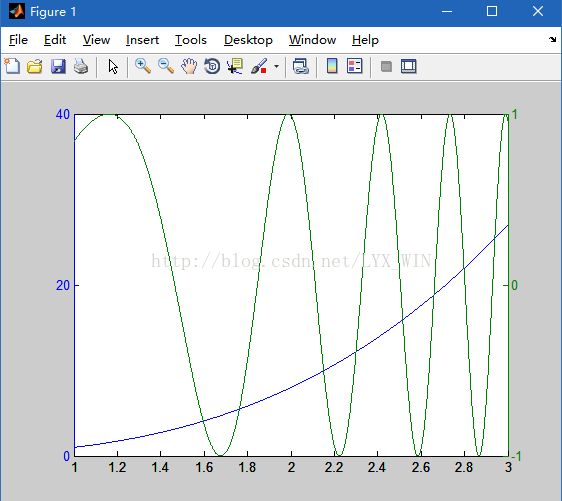
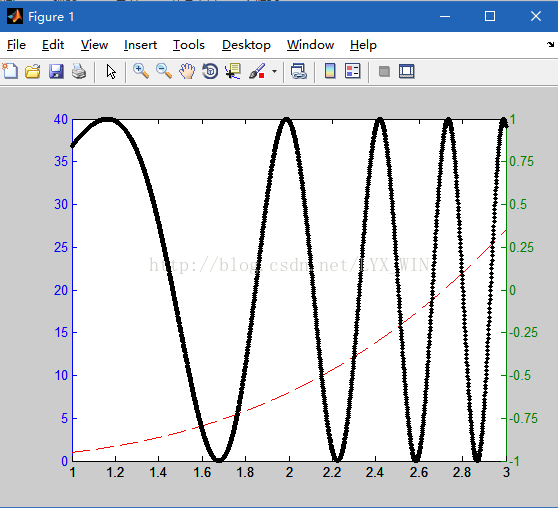
例.利用plotyy()函数检测上例中双纵坐标图性质,并利用set()函数对双坐标轴和曲线属性进行设置。
>> x=1:0.001:3;
>> y1=x.^3;
>> y2=sin(y1);
>> [AX,H1,H2]=plotyy(x,y1,x,y2,'plot')
AX =
173.0018 175.0018
H1 =
174.0028
H2 =
176.0023
>> set(AX(1),'YTick',[0 5 10 15 20 25 30 35 40])
>> set(AX(2),'YTick',[-1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1])
>> set(H1,'LineStyle','--','Color','r')
>> set(H2,'LineStyle','.','Color','k')
Warning: Setting marker type based on 'LineStyle' property
"" 'Marker' and 'LineStyle' have been made separate properties
"" Use 'Marker' property to remove this warning
(7)Easy绘图命令
a.fplot()函数
| 模式 |
说明 |
| fplot(fun,limits,tol,LineSpec) |
以一定的方式绘制fun()函数图形。fun()为函数名或函数句柄;limits为坐标轴的范围,形式为[xmin xmax ymin ymax];tol为函数的误差范围,默认为2e-3;LineSpec为绘图曲线的性质,如线型、颜色和标记点等 |
| fplot(fun,limits,n) |
若n>=1,则取点为n+1绘制fun()函数图形;若缺省则系统默认为1.在此情况下,最大极限范围为(1/n)*(xmax-xmin) |
| [X,Y]=fplot(fun,limits) |
系统根据情况取定画图点,并将坐标轴返回到X,Y中。此命令不会绘制图形,只是取点。然而,用户可以通过函数plot(X,Y,...)进行绘图 |
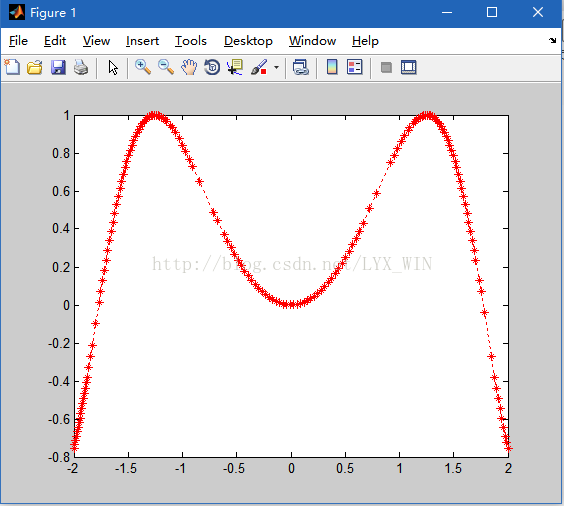
例.利用fplot()函数绘图图形
>> fn=@(x)sin(x^2);
>> fplot(fn,[-2,2],':r*')
b.ezplot()函数和ezpolar()函数
| 格式 |
说明 |
| ezplot(fun) |
在系统默认区间[-2π,2π]范围绘制fun()函数的曲线图像 |
| ezplot(fun,[mix,max]) |
在用户自定义的区间[min,max]内绘制fun()函数的曲线图像 |
| ezplot(fun,[min,max],fig) |
在用户指定的函数绘制窗口和自定义的区间[min,max]下,绘制fun()函数的曲线图像 |
例.利用ezplot()函数绘制![]() 的函数图形,利用ezpolar()函数绘制y=cos(t-2)/t的函数图形
的函数图形,利用ezpolar()函数绘制y=cos(t-2)/t的函数图形
>> syms t
>> y=(3*sin(2*t+1))/(4*exp((2*t)/3));
>> ezplot(y,[0,3*pi])
>> grid on
2.三维图形绘制
(1)曲线图绘制
| 格式 |
说明 |
| plot3(X,Y,Z,’S’) |
利用坐标值函数在三维图形框中绘制出相应的图形,’S’为绘图曲线性质,如线型、颜色和标记点等 |
| plot3(X,Y,Z,’S’,’ProperyName’,Porperty Value) |
利用坐标值函数在三维图形框中绘制出相应的图形,并对图形属性进行设置 |
| h=plot3(X,Y,Z,’S’) |
利用plot3函数绘制图形,同时返回图形句柄 |
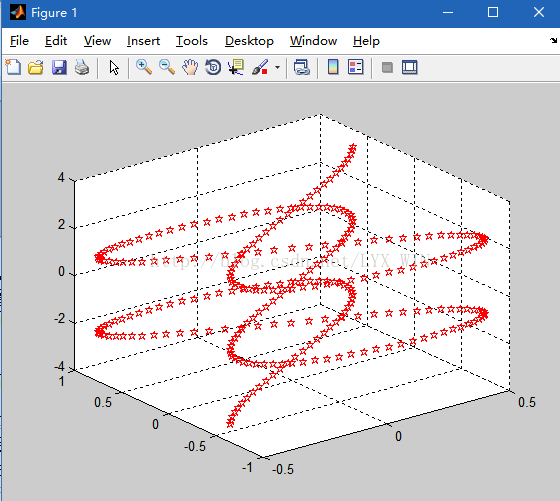
例.利用plot3()函数绘制三维图形,其坐标为(cos(2t)sin(t),sin(2t),t),并对所绘制的图形属性进行设置。
>> t=-1.1*pi:0.008*pi:1.1*pi;
>> plot3(cos(2*t).*sin(2*t),sin(2*t),t,'rp')
>> grid on
(2)网络图绘制
mesh(X,Y,Z):最常用的网络图调用形式,图形的颜色深浅与z的高度成正比。若X、Y均为向量,X、Y的长度分别为m、n,则矩阵Z的大小就为mXn;若X、Y为矩阵,则![]() 为网络线的交点。
为网络线的交点。
mesh(Z):上一个表达式中的XY缺省时,若矩阵Z的大小为mXn,则X=1:n,Y=1:m,其余的同上。
mesh(X,Y,Z,C):最完整的网络图调用形式,以矩阵C来进行颜色设置,若XYZ均为矩阵,则其要求与C拥有相同的维度。
meshc():在网络线的下方绘制一个等值线图。
meshz():在网格线的周围绘制一个窗帘图
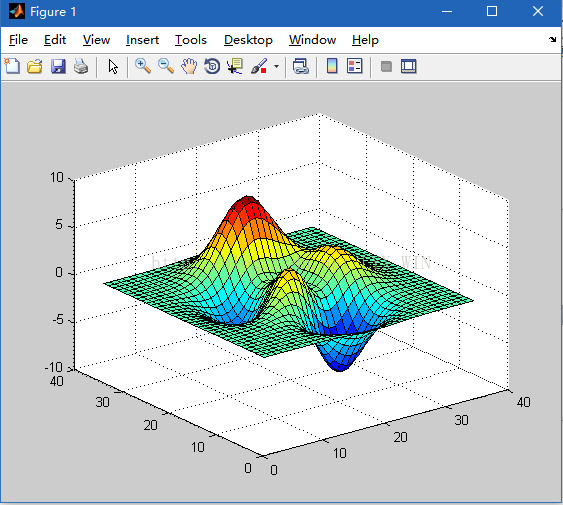
例.利用mesh()函数绘制peaks(35)函数图形
>> z=peaks(35);
>> mesh(z)
>> meshc(z)
(3)曲面图绘制
shading faceted:在绘制曲面是采用分层网络线,并填充默认值颜色
shading flat:表示平滑式颜色分布方式;去掉黑色线条,补片保持单一颜色。
shading interp:表示插补式颜色分布方式;同样去掉线条,但补片以插值加色。这种方式需要比分块和平滑更多的计算量。
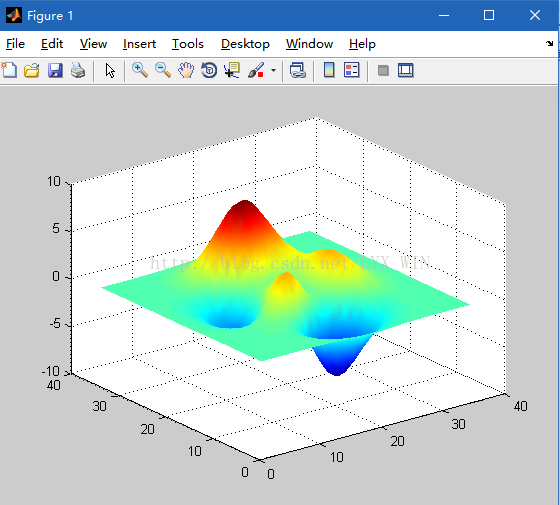
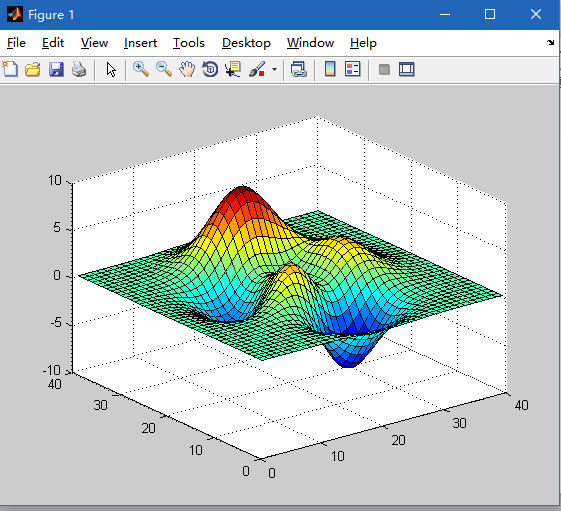
例.使用surf()函数绘制peaks(35)函数图形
>> z=peaks(35);
>> surf(z)
>> shading flat
>> shading interp
(4)绘制等值线图
| 格式 |
说明 |
| contour(z,s) |
以z为等值线的数值绘图等值线图,s为等值线的属性,如线型、颜色等 |
| contour(z,n) |
按用户要求绘图等值线,n为所画等值线的条数,MATLAB会根据条数和函数值分配等值线的数值 |
| contour(z,v) |
按照向量v和函数值分配等值线数值间隔,并依次绘制等值线图 |
| [c,h]=contour(z) |
返回等值线图形的等值线向量c和等值线句柄 |
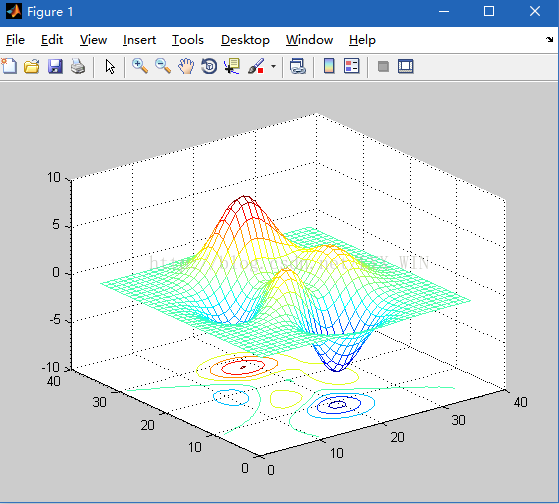
例.利用contour()函数绘制peaks(35)的等值线图
>> z=peaks(35);
>> mesh(z)
>> hold
Current plot held
>> contour3(z,4,'-k')
3.特别图形绘制
(1)区域图绘制
格式:area(X,Y,’PropertyName’,PropertyValue,)
其中,当X,Y均为行向量时,其结果等同于plot(X,Y);当X为行向量,Y为矩阵时,以X为横坐标绘制矩阵Y,每列累计数值为纵坐标绘制图形。当Y缺省时,默认Y为X的下标组成的行向量。
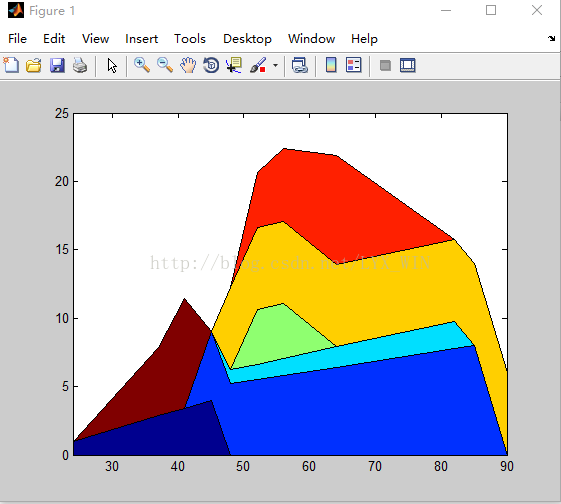
例.利用区域绘图函数area()绘制区域图,其中x=[24,45,48,56,48,64,41;45,85,82,52,90,52,37]、
y=[1,5,1,4,6,8,8;4,8,2,4,6,4,5]。
>> x=[24,45,48,56,48,64,41;45,85,82,52,90,52,37];
>> y=[1,5,1,4,6,8,8;4,8,2,4,6,4,5];
>> area(x,y)
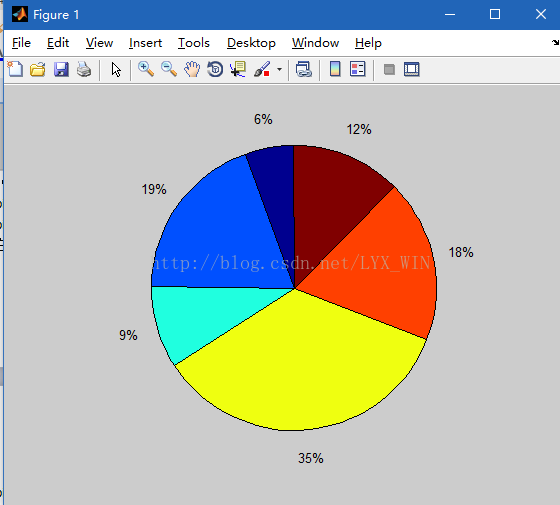
(2)饼图绘制
pie(x):绘制向量x的饼图,向量x的每一个元素就是饼图中的一个扇形
pie(x,explode):explode和x是维度相同的矩阵,如果explode中有非零元素,x中对应的元素在饼图中的图形就会外移突出,加强强调
pie(x,labels):用labels来定义标识对应饼图扇形部分。当缺省时则为各部分所占百分比
例.在x=[24,84,40,152,80,54]情况下,利用pie()函数绘制饼图
>> x=[24,84,40,152,80,54];
>> pie(x)
(3)直方图和梯形图
格式:bar(X,Y,width,’style’)
其中,width用于设置直方图条形的相对宽度和条形之间的间距;style设置条形的形状类型,如group、stack和detached等。
例.利用直方图和梯形图表示数据y=sin(x)的分布情况,其中x=-pi:0.1pi:pi。
>> x=-pi:0.1*pi:pi;
>> y=sin(x);
>> bar(x,0.5,'r')
>> stairs(y)
(4)矢量分布绘制
| 格式 |
说明 |
| quiver(x,y,u,v) |
使用(x,y)为指定点用箭头代表的矢量方向来绘制向量,u和v是对应的方向递增量。其中,x,y,u和v的维度必须是相同的 |
| quiver(u,v,scale) |
在默认的x-y的坐标系中绘制向量,u和v是对应的发现递增量.scale是用来设定向量图中的箭头长度 |
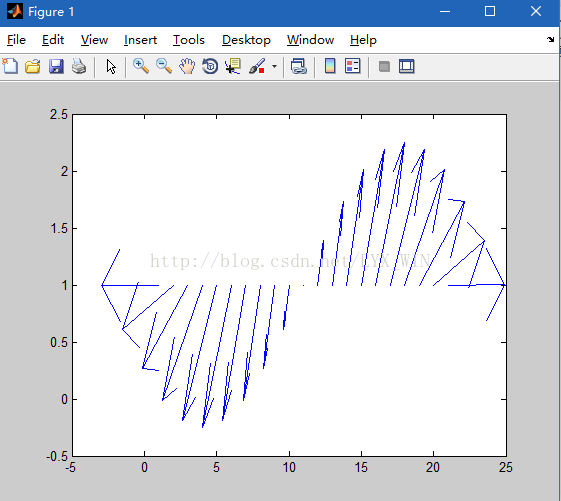
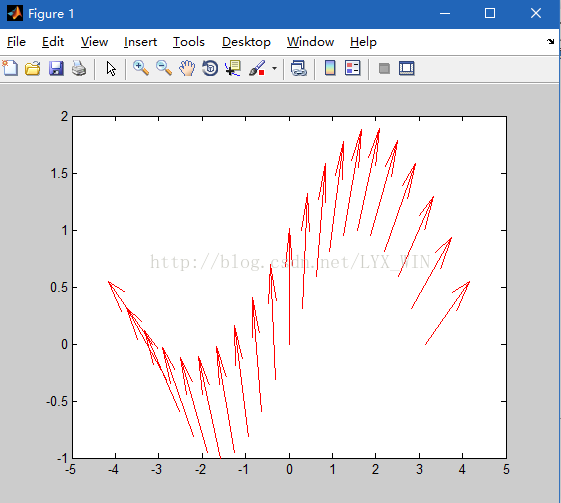
例.绘出x=-pi:0.1*pi:pi、y=sin(x)以及u=-1:0.1:1、cos(u)之间的矢量分布图
>> x=-pi:0.1*pi:pi;
>> y=sin(x);
>> u=-1:0.1:1;
>> v=cos(u);
>> quiver(x,y)
>> quiver(x,y,u,v,0.8,'r')
(5)离散数据图绘制
| 格式 |
说明 |
| stem(x) |
绘制x的离散数据图,系统自动等间距绘制离散线 |
| stem(x,y,’s’) |
以x为横坐标,以y为纵坐标绘制离散点,并将离散点和横轴垂直连接。s为离散线的属性,如线型、颜色和点型 |
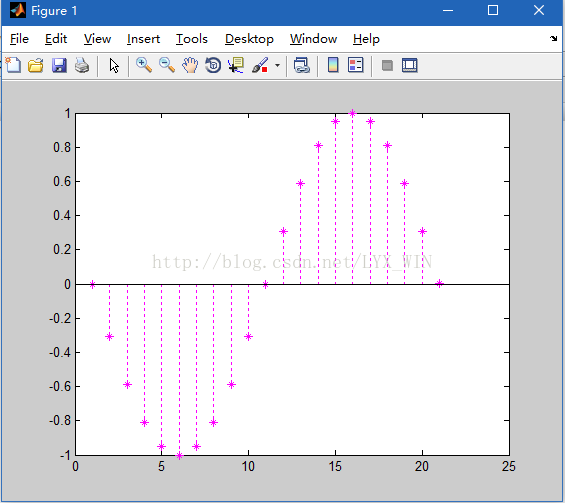
例.绘制y=sin(x)的离散数据图,其中x=-pi:0.1pi:pi
>> x=-pi:0.1*pi:pi;
>> y=sin(x);
>> stem(y,':m*')
(6)误差线图形绘制
| 格式 |
说明 |
| errorbar(x,y,e) |
根据x,y绘制曲线,在每点 |
| errorbar(x,y,u,d) |
根据x,y绘制曲线,在每点 |
| errorbar(...,’s’) |
s为曲线属性,如线宽、标记点和颜色等 |
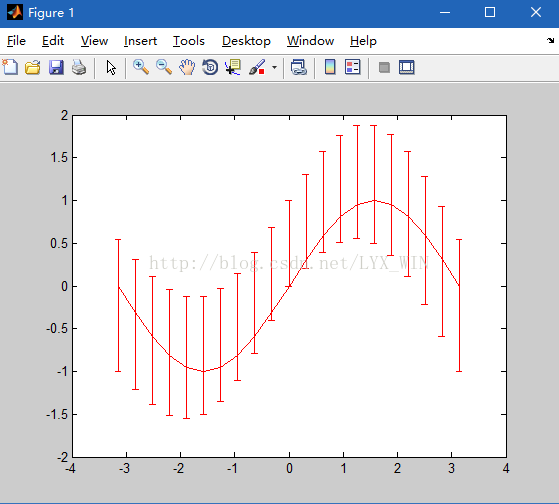
例.利用errorbar()函数绘制x=-pi:0.1pi:pi、y=sin(x),上误差为u=-1:0.1:1,下误差为v=cos(u)的误差图
>> x=-pi:0.1*pi:pi;
>> y=sin(x);
>> u=-1:0.1:1;
>> v=cos(u);
>> errorbar(x,y,u,v,'-r')
(7)伪色彩图绘制
| 格式 |
说明 |
| pcolor(x) |
绘制x为颜色矩阵的伪彩色图 |
| pcolor(x,y,c) |
在坐标系中的(x,y)点以颜色c为伪彩色矩阵绘制伪彩色图 |
(8)极坐标图形绘制
格式:polar(theta,rho,LineSpac)
其中,theta为角度,rho为半径,LineSpac为曲线属性,如颜色、线型和标记点
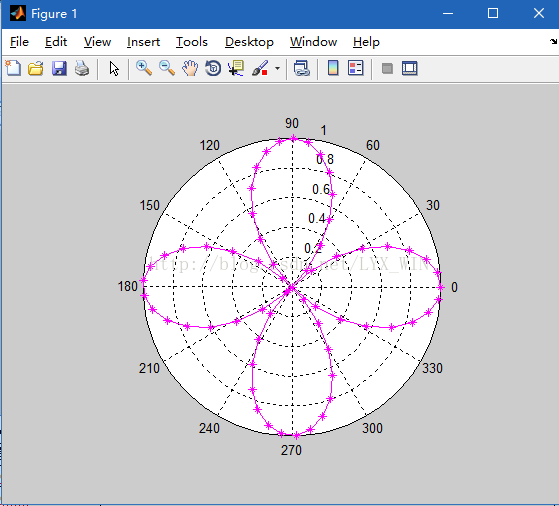
例.利用polar()函数绘制y=cos(2x)极坐标图,其中x=0:0.1:2pi
>> x=0:0.1:2*pi;
>> y=cos(2*x);
>> polar(x,y,'-m*')
4.图形处理
(1)图形标注
title(s):在图形的上部书写图名
xlabel(s):在横轴处书写横坐标标名
ylabel(s):在纵坐标处书写纵坐标标名
text(x,y,s):在(x,y)处书写字符注释
legend(s1,s2,...):在图形的右上角书写图例注释
例.利用标注方法对吐血进行标注.图形喂y1=exp(0.6.^x)-1.7;y2=sin(x*3),其中x=0:0.05:5
>> x=0:0.05:5;
>> y1=exp(0.6.^x)-1.7;
>> y2=sin(x*3);
>> plot(x,y1,x,y2,'m:')
>> xlabel('input:x','fontsize',20)
>> ylabel('output:y','fontsize',15)
>> legend('y1=exp(0.4.^x)-1.5','y2=sin(x*4)')
>> grid on
(2)坐标轴的控制
a.分隔线
grid on:在图形中画出分格线
grid off:在图形中不画不画分格线
box on:当前图形坐标呈现封闭状态
box off:当前图形坐标呈现开启状态
b.坐标轴控制
| 命令 |
说明 |
命令 |
说明 |
| axis auto |
坐标轴采用默认设置 |
axis equal |
等长刻度横纵坐标系 |
| axis ij |
矩阵式坐标系 |
axis normal |
缺省矩形坐标系 |
| axis xy |
普通直角坐标系 |
axis square |
正方形坐标系 |
| axis(V) V=[x1,x2,y1,y2] V=[x1,x2,y1,y2,z1,z2] |
用户自定义坐标范围(二维三维均可)。其中,x1,x2为横轴的范围值,其他类似 |
axis tight |
坐标范围由数据大小自动取定 |
| axis image |
等长刻度横纵坐标系,且坐标框紧贴数据范围 |
(3)图形的打印和输出
a.图形输出命令print
| 命令 |
说明 |
| |
将当前图形窗口的一个高分辨率图形复制发送至打印机。这要求将print命令分配给打印机 |
| print filename |
将当前图形窗口的图形复制保存到文件filename中 |
| print(handle,’filename’) |
将图形句柄和文件名复制发送至可以使用的打印机 |
| [pcmd,dev]=printopt |
将用户输入的命令和设备选择,返回str、dev。此时有可能要修改这个M文件 |
b.纸张方向控制命令
| 命令 |
说明 |
| orient landscape |
将下次的打印方向设置为landscape,即水平方向 |
| orient portrait |
将下次的打印方向设置为portait,即竖直方向 |
| orient tall |
将下次的打印方向设置喂竖直方向,并将打印纸设置为离边框0.25英寸的地方打印 |
| orient |
将当前的打印方向返回一个字符串中,并显示在命令框中 |
5.图形窗口
(1)图形窗口的创建与控制
| 窗口名 |
命令 |
操作 |
| 图形面板(Figure Palette) |
figurepalette |
选择【View】 |
| 绘图浏览器(Plot Browser) |
plotbrowser |
选择【View】 |
| 属性编辑器(Property Editor) |
propertyeditor |
选择【View】 |
例.创建图形窗口,并打开各绘图窗口
>> figure
>> x=peaks(40);
>> surf(x)