“随机森林”及“混合随机森林和多目标粒子群优化”（RF_MOPSO），以预测目标作为学习方法并分别找到多特征过程的最佳参数（Matlab代码实现）

 欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

1 概述

2.1 算例1

2.2 算例2

3 参考文献

‍4 Matlab代码实现

---

1 概述

      多目标优化问题普遍涉及到工程设计、生产制造、信息处理等应用领域。粒子群优化算法具有快速收敛、简单易行、并行搜索等特点，特别适合处理多目标优化问题。本文对多目标粒子群优化算法进行系统性的研究，结合随机森林​的优势。包括"随机森林"和“混合随机森林和多目标粒子群优化”(RF_MOPSO)，以预测目标作为学习方法并分别找到多特征过程的最佳参数。其中一个算例是钻孔过程预测和优化。采用随机森林与多目标粒子群优化算法相结合的方法辅助优化工艺参数选择。

摘要

本文研究了随机森林（Random Forest, RF）及其与多目标粒子群优化（Multi-Objective Particle Swarm Optimization, MOPSO）相结合的方法（RF_MOPSO），用于多特征过程的最佳参数优化。随机森林作为一种强大的集成学习算法，能够有效处理高维数据并评估特征重要性。然而，在复杂的多目标优化问题中，RF的参数选择和模型性能优化仍面临挑战。多目标粒子群优化算法（MOPSO）具有快速收敛和全局搜索能力强的特点，适用于处理多目标优化问题。本文将RF与MOPSO相结合，通过MOPSO优化RF的超参数，以提高模型的预测精度和稳定性。实验结果表明，RF_MOPSO在多个算例中均表现出优越的性能。

1. 引言

在许多实际应用中，如工程设计、生产制造和信息处理等领域，多目标优化问题普遍存在。随机森林（RF）作为一种集成学习方法，因其在处理高维数据和特征选择方面的优势而被广泛应用。然而，RF的超参数选择对模型性能有显著影响。多目标粒子群优化算法（MOPSO）是一种基于群体智能的优化算法，能够有效处理多目标优化问题。本文提出了一种混合方法（RF_MOPSO），通过MOPSO优化RF的超参数，以提高模型在多特征过程中的预测性能。

2. 随机森林（RF）

随机森林是一种基于决策树的集成学习算法，通过构建多个决策树并集成其结果来提高预测精度。RF的主要优点包括：

• 高预测精度：通过集成多个决策树的结果，RF能够显著提高模型的预测精度。

• 特征重要性评估：RF可以评估每个特征对目标变量的重要性，为特征选择提供依据。

• 处理高维数据：RF能够有效处理高维数据，即使在特征数量远大于样本数量的情况下也能表现良好。

3. 多目标粒子群优化算法（MOPSO）

MOPSO是一种基于群体智能的优化算法，通过模拟粒子群的行为来寻找最优解。MOPSO的主要特点包括：

• 快速收敛：MOPSO能够快速收敛到最优解，适合处理复杂的优化问题。

• 全局搜索能力：MOPSO通过粒子之间的信息交互，能够有效避免局部最优，具有较强的全局搜索能力。

• 多目标优化：MOPSO能够同时优化多个目标，适用于多目标优化问题。

4. 混合随机森林和多目标粒子群优化（RF_MOPSO）

本文提出的RF_MOPSO方法结合了RF的预测能力和MOPSO的优化能力，通过MOPSO优化RF的超参数，以提高模型的预测精度和稳定性。具体步骤如下：

1. 初始化：随机生成一组粒子，每个粒子代表RF的一个超参数组合。

2. 评估：使用RF模型对每个粒子的超参数组合进行评估，计算其适应度函数（如均方根误差、平均绝对误差等）。

3. 更新：根据粒子的适应度值，更新粒子的位置和速度，寻找最优解。

4. 优化：重复上述步骤，直到达到最大迭代次数或满足收敛条件。

5. 实验与结果

为了验证RF_MOPSO的有效性，本文进行了多个算例的实验，包括钻孔过程预测和优化。实验结果表明，RF_MOPSO在多个算例中均表现出优越的性能，能够有效提高RF模型的预测精度和稳定性。例如，在钻孔过程预测中，RF_MOPSO模型的均方根误差（RMSE）和平均绝对误差（MAE）均优于传统的RF模型。

6. 结论

本文提出了一种基于随机森林和多目标粒子群优化（RF_MOPSO）的方法，用于多特征过程的最佳参数优化。实验结果表明，RF_MOPSO能够有效提高RF模型的预测精度和稳定性，适用于复杂的多目标优化问题。未来的工作将进一步优化RF_MOPSO的参数设置，提高其在更大规模数据集上的性能。

2 运行结果

2.1 算例1

算例1主函数代码： 

clc
clear
close all; 

%Loading
load data1.csv
[TrainData,TestData] = ManageData(data1);
train_x = TrainData.Feature;
target = TrainData.Lebel;
test_x = TestData.Feature;
test_y = TestData.Lebel ;
data1 = train_x(:,1);
data2 = train_x(:,2);
data3 = train_x(:,3);
data4 = train_x(:,4);
data5 = train_x(:,5);

X = table(data1,data2,data3,data4,data5,target);
rng('default'); % For reproducibility

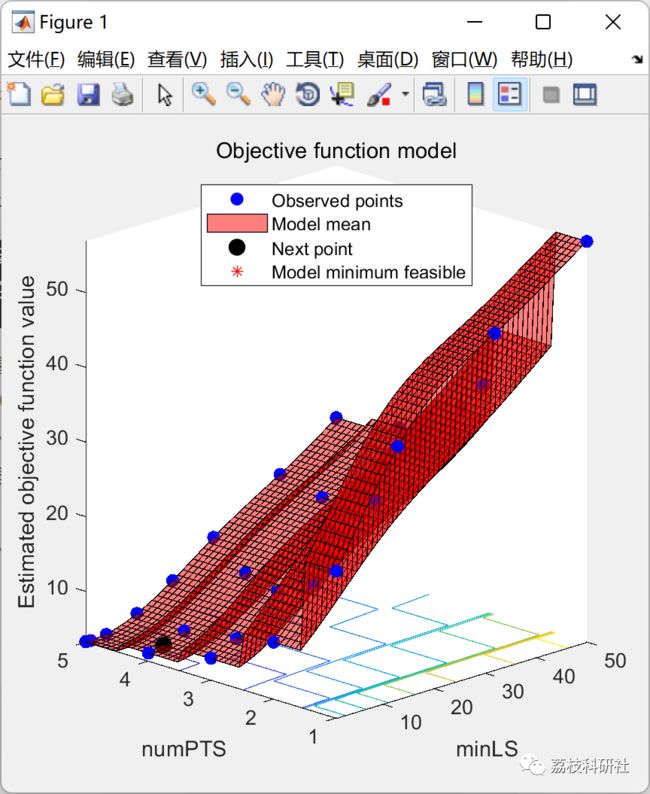
%%Specify Tuning Parameters
maxMinLS = 50;
minLS = optimizableVariable('minLS',[1,maxMinLS],'Type','integer');
numPTS = optimizableVariable('numPTS',[1,size(X,2)-1],'Type','integer');
hyperparametersRF = [minLS; numPTS];

%Minimize Objective Using Bayesian Optimization
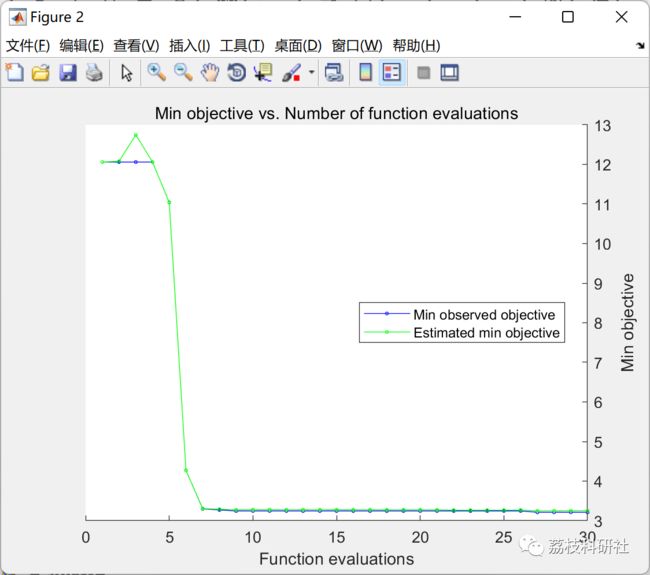
results = bayesopt(@(params)oobErrRF(params,X,target),hyperparametersRF,...
    'AcquisitionFunctionName','expected-improvement-plus','Verbose',0);

bestOOBErr = results.MinObjective
bestHyperparameters = results.XAtMinObjective

%Train Model Using Optimized Hyperparameters
Mdl = TreeBagger(450,train_x,target,'OOBPred','On','Method','regression',...
    'MinLeafSize',bestHyperparameters.minLS,...
    'NumPredictorstoSample',bestHyperparameters.numPTS);

predicted_train = oobPredict(Mdl);
predicted_test = predict(Mdl,test_x);
trainmse = sum((predicted_train-target).^2)/length(target);
testmse = sum((predicted_test-test_y).^2)/length(test_y);

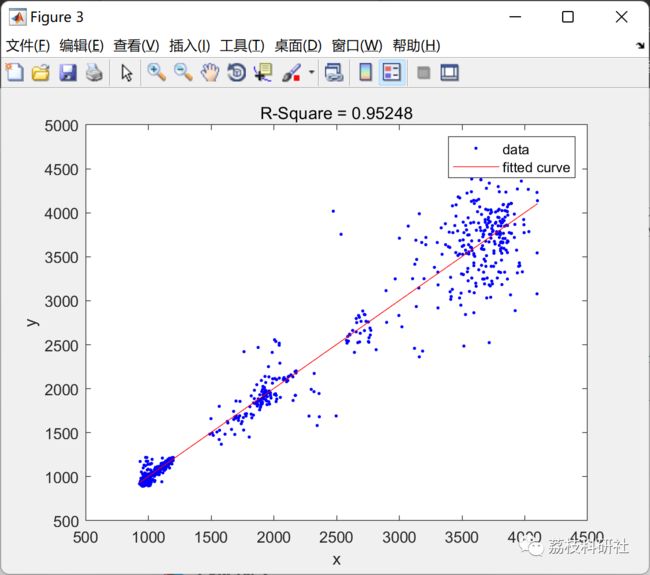
[fitresult.train, gof.train] = fit( predicted_train, target, 'poly1' );
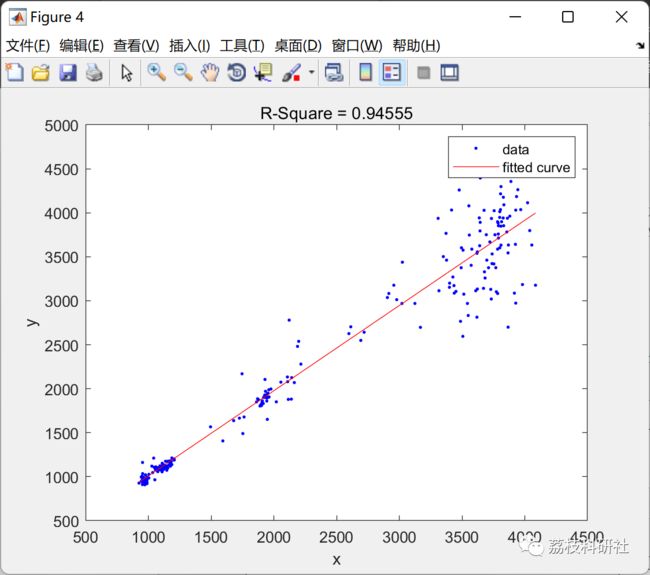
[fitresult.test, gof.test] = fit( predicted_test, test_y, 'poly1' );
b = gof.train.rsquare;
c = gof.test.rsquare;

figure
plot(fitresult.train,predicted_train,target)
hold on
title(['R-Square = ' num2str(b)])

figure
plot(fitresult.test,predicted_test,test_y)
hold on
title(['R-Square = ' num2str(c)])

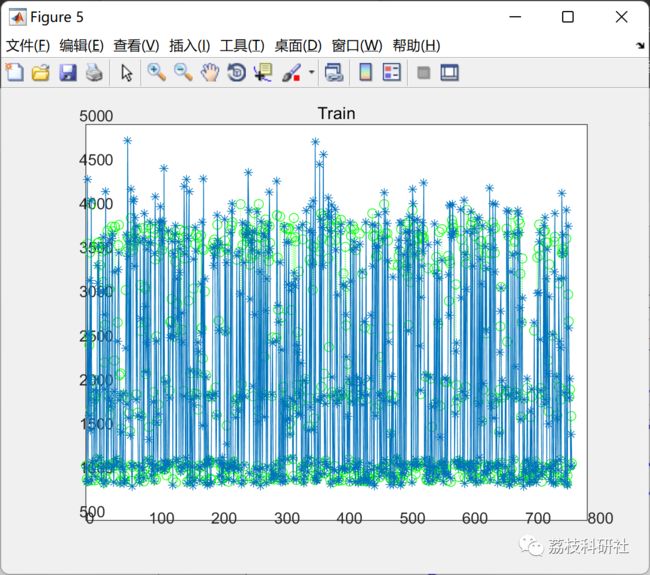
figure
plot(predicted_train,':og')
hold on
plot(target,'- *')
title('Train')

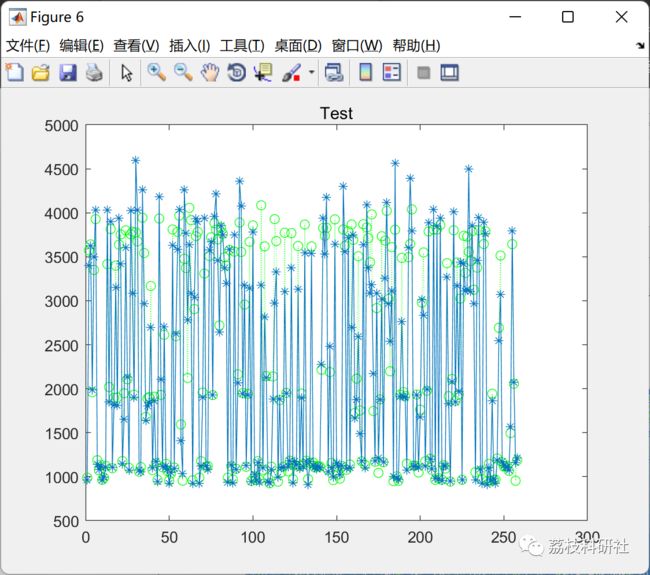
figure
plot(predicted_test,':og')
hold on
plot(test_y,'- *')
title('Test')

MAPE.train = mean((abs(predicted_train-target))./target).*100;
MAPE.test = mean((abs(predicted_test-test_y))./test_y).*100;

Vmse.train=errperf(target,predicted_train,'mse');
Vmse.test=errperf(test_y,predicted_test,'mse');
RMSE.train=sqrt(Vmse.train);
RMSE.test=sqrt(Vmse.test);
 

2.2 算例2

3 参考文献

[1]尹丹. 多目标粒子群优化算法的改进与应用[D].扬州大学,2021.DOI:10.27441/d.cnki.gyzdu.2021.001684.

[2]陈文涛. 基于自适应分解多目标粒子群优化的特征选择方法研究[D].江苏大学,2021.DOI:10.27170/d.cnki.gjsuu.2021.000867.

‍4 Matlab代码实现