二叉树的一些常见基本面试题
1.使用非递归地方式来完成二叉树的先序、中序、后序遍历
(1)
使用非递归地方式来完成二叉树的先序遍历
通过栈来实现
首先先将根节点入栈,然后循环,取出栈顶元素为当前元素,并打印当前元素,再将当前元素的右子树和左子树先后入栈,再重复之前的操作,直到栈为空,循环结束,详细操作见图(竖向来看)
340 //先序
341 void TreePreOrderByLoop(TreeNode* root)
342 {
343 if(root == NULL)
344 {
345 return ;
346 }
347 //1.先把根节点入栈
348 SeqStact stack;
349 SeqStactInit(&stack);
350 SeqStactPush(&stack,root);
351 //2.循环开始,若栈为空,循环结束
352 TreeNode* cur=NULL;
353 while(SeqStactTop(&stack,&cur))
354 {
355 //a)取栈顶元素为当前元素
356 //b)出栈
357 SeqStactPop(&stack);
358 //c)访问当前元素,即打印当前元素
359 printf("%c",cur->data);
360 //d)把当前元素的右子树入栈
361 if(cur->rchild!=NULL)
362 {
363 SeqStactPush(&stack,cur->rchild);
364 }
365 //e)把当前元素的左子树入栈
366 if(cur->lchild!= NULL)
367 {
368 SeqStactPush(&stack,cur->lchild);
369 }
370 }
371 printf("\n");
372 return;
373 }
374
(2)使用非递归地方式来完成二叉树的中序遍历
通过栈来实现
首先先要定义一个cur指针来指向根节点,来循环地将cur指向cur地左孩子,并将cur入栈,若cur为空,就出栈并打印,再将cur指向该节点的右子树,循环这个操作,详细过程如图
375 //非递归地实现中序遍历
376 void TreeInOrderByLoop(TreeNode* root)
377 {
378 if(root == NULL)
379 {
380 return ;
381 }
382 //1.定义一个cur指针
383 SeqStact stack;
384 SeqStactInit(&stack);
385 TreeNode* cur=root;
386 while(1)
387 {
388 //2.循环地判断cur是否为NULL
389 //若cur!=NULL,则cur入栈,并cur=cur->lchild
390 while(cur != NULL)
391 {
392 SeqStactPush(&stack,cur);
393 cur=cur->lchild;
394 }
395 //3.若cur=NULL取栈顶元素,访问并出?
396 TreeNode* top = NULL;
397 int ret=SeqStactTop(&stack,&top);
398 if(ret == 0)
399 {
400 //此时说明?中没有元素遍历
401 printf("\n");
402 return ;
403 }
404 printf("%c",top->data);
405 SeqStactPop(&stack);
406 //4.让cur=cur->rchild,重复刚才对循环过程
407 cur=top->rchild;
408 }
409 return ;
410 }
411
(3)使用非递归地方式来完成二叉树的后序遍历
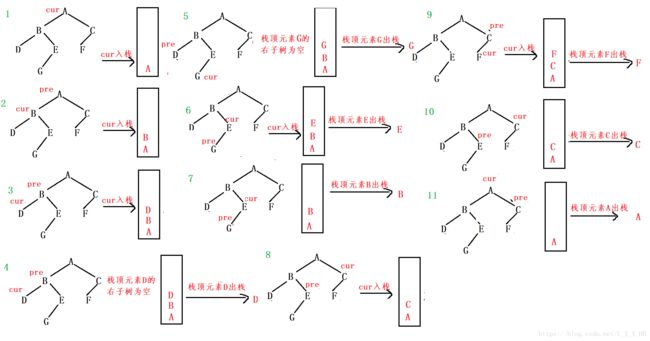
通过栈来实现,首先先定义一个指针cur指向根节点,一个pre指向上一个位置,然后循环地将cur指向cur的左孩子,并且入栈,直到cur为空就取栈顶元素,再对栈顶元素进行判断,若栈顶元素的右孩子=上一个元素,或栈顶元素的右孩子为空才能访问栈顶元素,并进行出栈操作,若不满足上面的条件,就让cur指向栈顶的右子树,循环判定
412 //非递归地实现后序遍历
413 void TreePostOrderByLoop(TreeNode* root)
414 {
415 if(root == NULL)
416 {
417 return ;
418 }
419 //1.定义一个指针cur指向根节点root
420 TreeNode* cur=root;
421 TreeNode* pre=NULL;//保存着上一个访问过的元素
422 SeqStact stack;
423 SeqStactInit(&stack);
424 while(1)
425 {
426 //2.循环判定cur是否为NULL
427 //若cur!= NULL,则cur入栈,cur=cur->lchild
428 while(cur!=NULL)
429 {
430 SeqStactPush(&stack,cur);
431 cur=cur->lchild;
432 }
433 TreeNode* top = NULL;
434 int ret = SeqStactTop(&stack,&top);
435 if(ret == 0)
436 {
437 printf("\n");
438 return ;
439 }
440
441 //3.若cur==NULL,循环取栈定元素
442 //4.对栈顶元素进行判定
443 //若栈顶元素的rchild=上一个元素,栈顶元素的rchild==NULL,才能访问栈顶元素,同时进行出栈
444 //5.若不满足上面的条件,则让cur指向栈顶的右子树,循环判定
445 if(top->rchild == NULL || top->rchild == pre)
446 {
447 printf("%c",top->data);
448 SeqStactPop(&stack);
449 pre=top;
450 }
451 else
452 {
453 cur=top->rchild;
454 }
455 }
456 return;
457 }
458
2.二叉树的镜像操作
镜像
(1)递归实现
459 //二叉树的镜像(递归实现)
460 void Swap(TreeNode** a,TreeNode** b)
461 {
462 TreeNode* tmp=*a;
463 *a=*b;
464 *b=tmp;
465 return;
466 }
467 void TreeMirror(TreeNode* root)
468 {
469 if(root == NULL)
470 {
471 return ;
472 }
473 //访问动作就是交换左右子树
474 Swap(&root->lchild,&root->rchild);
475 TreeMirror(root->lchild);
476 TreeMirror(root->rchild);
477 return;
478 }
479
(2)非递归实现
利用非递归实现的先序、中序、后序操作,将访问操作,打印改为Swap交换操作即可
480 //二叉树的镜像(非递归实现)
481 void TreeMirrorByLoop(TreeNode* root)
482 {
483 if(root == NULL)
484 {
485 return;
486 }
487 SeqQueue queue;
488 SeqQueueInit(&queue);
489 SeqQueuePush(&queue,root);
490 TreeNode* cur = NULL;
491 while(SeqQueueFront(&queue,&cur))
492 {
493 //此处的访问相当于交换左右子树
494 Swap(&cur->lchild,&cur->rchild);
495 SeqQueuePop(&queue);
496 if(cur->lchild != NULL)
497 {
498 SeqQueuePush(&queue,cur->lchild);
499 }
500 if(cur->rchild != NULL)
501 {
502 SeqQueuePush(&queue,cur->rchild);
503 }
504 }
505 return ;
506 }
507
3.判断一棵树是否为完全二叉树
完全二叉树:层序遍历,第一阶段,都有任何一个节点都同时具有左右子树,一旦发现某个节点不是同时具备左右子树,就进入第二阶段,任何一个节点必须没有左右子树
下面为完全二叉树的所有情况
508 //判断一棵树是否为完全二叉树
509 //首先要层序遍历,遍历过程分为两个阶段
510 //阶段一:
511 //任何一个节点同时有左右子树,一旦发现某个节点不是同时具备这个条件,进入阶段二
512 //a)当前节点只有右子树,一定不是完全二叉树
513 //b)若当前节点只有左子树,进入阶段二
514 //c)若当前节点没有子树,进入阶段二
515 //阶段二:
516 //任何一个节点必须没有子树
517 int IsCompleteTree(TreeNode* root)
518 {
519 if(root == NULL)
520 {
521 return 0;
522 }
523 SeqQueue queue;
524 SeqQueueInit(&queue);
525 SeqQueuePush(&queue,root);
526 //表示是否要进入第二阶段
527 int if_start_step_two_flag=0;
528 TreeNode* cur=NULL;
529 while(SeqQueueFront(&queue,&cur))
530 {
531 SeqQueuePop(&queue);
532 if(if_start_step_two_flag == 0)
533 {
534 //进入阶段一
535 if(cur->lchild != NULL && cur->rchild != NULL)
536 {
537 //同时具有左右子树
538 SeqQueuePush(&queue,cur->lchild);
539 SeqQueuePush(&queue,cur->rchild);
540 }
541 else if(cur->lchild == NULL && cur->rchild != NULL)
542 {
543 //当前只有右子树,没有左子树
544 return 0;
545 }
546 else if(cur->lchild != NULL && cur->rchild == NULL)
547 {
548 //当前只有左子树,没有右子树
549 if_start_step_two_flag = 1;
550 SeqQueuePush(&queue,cur->lchild);
551 }
552 else
553 {
554 //没有左右子树
555 if_start_step_two_flag = 1;
556 }
557 }
558 else
559 {
560 //进入阶段二
561 if(cur->lchild == NULL && cur->rchild == NULL)
562 {
563 ;
564 }
565 else
566 {
567 return 0;
568 }
569 }
570 //结束阶段一和阶段二
571 }
572 //循环结束
573 //所有节点都遍历完了,有没有return 0;,则一定是完全二叉树
574 return 1;
575 }
576
4.重建二叉树
根据二叉树的先序和中序或者中序和后序来重建二叉树
577 //根据二叉树的先序和中序遍历(或者后序和中序遍历)来重建二叉树
578 size_t Find(TreeNodeType arry[],size_t left,size_t right,TreeNodeType to_find)
579 {
580 size_t i = left;
581 for(;i= in_order_right)
598 {
599 //无效区间
600 //表示当前子树的中序遍历结果为空,说明这棵子树为空树
601 return NULL;
602 }
603 if(pre_order_index == NULL || *pre_order_index >= pre_order_size)
604 {
605 //pre_order_index == NULL 表示非法输入
606 //*pre_order_index >= pre_order_size 表示遍历结束
607 return NULL;
608 }
609 //根据先序遍历结果取出当前值,根据这个值构建出一个节点
610 //此时的new_node为当前树的根节点
611 TreeNode* new_node = CreateTreeNode(pre_order[*pre_order_index]);
612 //查找一下当前节点在在中序遍历中的位置
613 size_t cur_root_in_order_index = Find(in_order,in_order_left,in_order_right,new_node->data);
614 //该处断言表示cur_root_in_order_index一定不能为-1
615 assert(cur_root_in_order_index != (size_t)-1);
616 ++(*pre_order_index);
617 //左子树区间[in_order_left,cur_root_in_order_index)
618 new_node->lchild = _TreeRubuild(pre_order,pre_order_size,pre_order_index,in_order,in_order_left,cur_root _in_order_index);
619 //右子树区间[cur_root_in_order_index+1,in_order_right)
620 new_node->rchild = _TreeRubuild(pre_order,pre_order_size,pre_order_index,in_order,cur_root_in_order_inde x+1,in_order_right);
621 return new_node;
622 }
623 TreeNode* TreeRebuild(TreeNodeType pre_order[],TreeNodeType in_order[],size_t size)
624 {
625 size_t pre_order_index = 0;//下标
626 //表示一个前闭后开的区间,[in_order_left,in_order_right)
627 size_t in_order_left = 0;
628 size_t in_order_right = 0;
629 return _TreeRubuild(pre_order,size,&pre_order_index,in_order,in_order_left,in_order_right);
630 }