线性模型(linear model)
注:arg 是变元(即自变量argument)的英文缩写。
arg min 就是使后面这个式子达到最小值时的变量的取值
arg max 就是使后面这个式子达到最大值时的变量的取值形式:**f(**x)=w.x+b
参数解释:
x:列向量,n维表示样本的n种特征
w:为每个特征对应的权重生成的权重向量
案例:
以房价与房屋面积的例子引出线性回归问题,首先定义一些符号:
m:训练数据的大小
x:输入变量,是向量
y:输出变量,是实数
(x,y):一个训练实例
假设函数如下:

我们找出使这个函数最小的参数值,就得到了拟合训练的最佳参数。

公式6是针对只有一个训练实例的情况,这也被称为最小二乘法(LMS)。
考虑到所有m个训练实例,更新变化规则为:

运行这个规则直到收敛,就是批梯度下降算法。规则中的a是学习率,这个需要在实践中进行调整,其值过小会导致迭代多次才能收敛,其值过大会导致越过最优点发生震荡现象。
对于公式7的解法,当数据量较大时,每迭代一次就要遍历全部数据一次,这样会使运行变成龟速。解决方法如下:
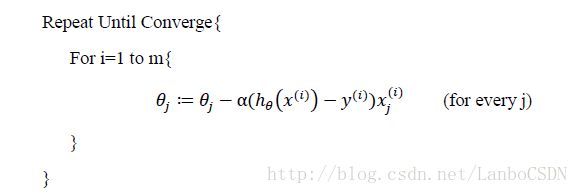
即更新参数时,不必遍历整个数据集,只需要一个实例便足够了。该算法可以达到很高的效果,但是会导致遍历次数增多,不能精确收敛到最优值等问题。该方法被称为增量梯度下降或随机梯度下降。
逻辑回归
对于目标值是连续变量的问题来说,使用线性回归效果不错。但对于目标值是离散变量的分类问题来说,有一定困难。
对于目标值是离散变量的两分类,假设目标值为{0,1},所以先改变模型使其预测值在[0,1]之间,我们选择这样一个函数:


其中,函数g被称为logistic函数或sigmoid函数。

注:上面公式第一行有错误
公式18与最小二乘法的形式一样,但实际上是不一样的,因为函数h不一样。
总结:逻辑回归就是一个被Logistic方程归一化后的线性回归,仅此而已。
线性判别分析(LDA)
训练时:设法将训练样本投影到一条直线上,使得同类样本的投影点尽可能接近、异类样本的投影点尽可能远离。要学习的就是这样一条直线。
预测时:将待预测样本投影到学到的直线上,根据它的投影点的位置来判定它的类别。
在scikit-learn中,LinearDiscriminantAnalysis实现了线性判别分析模型。其原型为:
class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(solver=’svd’,shrinkage=None,priors=None,n_components=None,store_covariance=False,tol=0.0001)
参数:
1、solver:一个字符串,指定求解最优化问题的算法
2、shrinkage:字符串’auto’或浮点数’None’。
3、priors:一个数组,数组中的元素依次指定了每个类别的先验概率。
4、n_components:一个整数,指定了数据降维后的维度。
5、store_covariance:一个布尔值。
6、tol:一个浮点值,它指定了svd算法中评判迭代收敛的阈值。
案例:
检查一下原始数据集在经过线性判别分析LDA之后的数据集的情况,给出绘制LDA降维之后的数据集(鸢尾花数据集)的函数:
def plot_LDA(converted_X,y):
'''
绘制经过 LDA 转换后的数据
:param converted_X: 经过 LDA转换后的样本集
:param y: 样本集的标记
:return: None
'''
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure()
ax=Axes3D(fig)
colors='rgb'
markers='o*s'
for target,color,marker in zip([0,1,2],colors,markers):
pos=(y==target).ravel()
X=converted_X[pos,:]
ax.scatter(X[:,0], X[:,1], X[:,2],color=color,marker=marker,
label="Label %d"%target)
ax.legend(loc="best")
fig.suptitle("Iris After LDA")
plt.show()然后调用该函数:
X_train,X_test,y_train,y_test=load_data()
X=np.vstack((X_train,X_test)
Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))
lda=discriminant_analysis.LinearDiscriminatAnalysis()
lda.fit(X,Y)
conveted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(converted_X,Y)执行结果如图所示:

可以看到经过线性判别分析之后,不同种类的鸢尾花之间的间隔较远;相同种类的鸢尾花之间相互聚集。
简单来说:LDA就是使同类样本的投影点尽可能接近,异类样本的投影点尽可能远离。