【语义分割论文阅读】Decoders Matter for Semantic Segmentation
1.(11)Decoders Matter for Semantic Segmentation
论文题目:Decoders Matter for Semantic Segmentation: Data-Dependent Decoding Enables Flexible Feature Aggregation
代码地址: https://github.com/LinZhuoChen/DUpsampling
推荐指数:★★★★☆
论文摘要:
采用编解码器结构的语义分割方法其解码器的最后一层通常采用双线性插值进行上采样得到最后像素级的预测结果。但是双线性插值法过于简单并且与数据无关容易导致最后得到次优解。作者提出一种新的数据相关的上采样方法Usampling.
1)在以原始输入的1/16or1/32大小的特征图作为输入,得到更加精确的分割结果。
2)可以灵活的与encoder组合
实验
1)PASCAL VOC:88.1%,30% computation·
2) PASCAL Context: 52.5%
1.1 方法概括
1.1 Introduction
编解码结构中采用backbone CNN作为编码器,解码器利用较低分辨率的特征图重建像素级预测结果,通常会用到bilinear upsampling,但是这种采样方式没有考虑每个预测像素之间的相关性。
解码器要求产生高分辨率的特征图以产生最后的预测结果,要求如下两点:
1)编码器中利用扩张卷积急剧减少输入图像的尺寸,计算复杂度和内存限制大规模数据的训练以及它的实时应用。
2)解码器通常要结合low-level feature map,而这一点限制了聚合特征的设计空间,很可能导致在解码器中产生次优的聚合特征。
本文利用分割标签的冗余性,证明了能够利用编码器产生的粗糙特征产生准确的分割结果.编码器结构无需继续过度减少特征图分辨率,减少了计算时间以及内存使用。此外成功分离混合特征以及最终的预测
1.1.2 思想
在语义分割中,计算损失通常是计算bilinear 上采样得到的结果,如下:
L ( F , Y ) = Loss ( softmax (bilinear ( F ) ) , Y ) ) \mathrm{L}(\mathbf{F}, \mathbf{Y})=\operatorname{Loss}(\text { softmax (bilinear }(\mathbf{F})), \mathbf{Y} ) ) L(F,Y)=Loss( softmax (bilinear (F)),Y))
其中, F F F是编码器处理的得到的特征图, Y Y Y是ground truth.
但是bilinear过于简单,影响重建质量。
作者的做法是:计算 Y ~ \tilde{\mathbf{Y}} Y~与 F F F之间的差异, Y ~ \tilde{\mathbf{Y}} Y~是 Y Y Y降低分辨率得到的结果。
为了将 Y Y Y压缩到 Y ~ \tilde{\mathbf{Y}} Y~,需要找到某一种尺度使得这种转化误差最小。
将 Y Y Y切成 H r × W r \frac{H}{r} \times \frac{W}{r} rH×rW个r*r大小的窗口,每一个窗口 S S S形为r*r*C,每个像素点值取值为[0,1],将每个 S S S拉伸为一个向量 V V V,其形为N=r*r*c.然后转化为低维向量 x x x,然后横向纵向的将之合并为 Y ~ \tilde{\mathbf{Y}} Y~.
转化方法为:
x = P v ; v ~ = W x \boldsymbol{x}=\mathbf{P} v ; \quad \tilde{\boldsymbol{v}}=\mathbf{W} \boldsymbol{x} x=Pv;v~=Wx
其中 P P P形为 C ~ × N \tilde{C} \times N C~×N,而 W W W形为 N × C ~ N \times \tilde{C} N×C~.
v ~ \tilde{\boldsymbol{v}} v~是真实标签 v v v经压缩后得到的结果.
最小化重建误差: P ∗ , W ∗ = arg min P , W ∑ v ∥ v − v ~ ∥ 2 = arg min P , W ∑ v ∥ v − W P v ∥ 2 \begin{array}{c}{\mathbf{P}^{*}, \mathbf{W}^{*}=\underset{\mathbf{P}, \mathbf{W}}{\arg \min } \sum_{\boldsymbol{v}}\|\boldsymbol{v}-\tilde{\boldsymbol{v}}\|^{2}} \\ {=\underset{\mathbf{P}, \mathbf{W}}{\arg \min } \sum_{\boldsymbol{v}}\|\boldsymbol{v}-\mathbf{W} \mathbf{P} \boldsymbol{v}\|^{2}}\end{array} P∗,W∗=P,Wargmin∑v∥v−v~∥2=P,Wargmin∑v∥v−WPv∥2
这个方程可以用SGD迭代优化,在正交性约束下,可以使用PCA求解。
将 Y ~ \tilde{\mathbf{Y}} Y~作为目标,利用回归损失计算压缩标签 Y ~ \tilde{\mathbf{Y}} Y~和真实值之间的误差:
L ( F , Y ) = ∥ F − Y ~ ∥ 2 \mathrm{L}(\mathbf{F}, \mathbf{Y})=\|\mathbf{F}-\tilde{\mathbf{Y}}\|^{2} L(F,Y)=∥F−Y~∥2
可以用 l 2 l2 l2损失计算上述误差,但是,更直接的的方式是在 Y Y Y空间计算loss值,利用学习到的重建矩阵 W W W对 F F F进行上采样,然后计算像素级的分类损失:
L ( F , Y ) = Loss ( softmax (DUpsample ( F ) ) , Y ) \mathrm{L}(\mathbf{F}, \mathbf{Y})=\operatorname{Loss}(\text { softmax (DUpsample }(\mathbf{F})), \mathbf{Y} ) L(F,Y)=Loss( softmax (DUpsample (F)),Y)
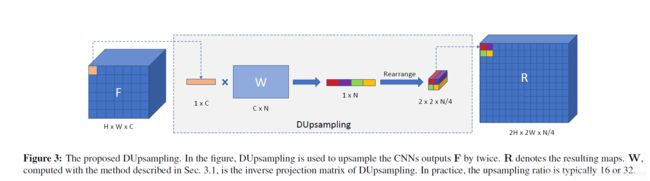
其中 F F F是编码器处理之后的特征图,利用真实标签与压缩值过程学习到的 W W W处理,如上图,将 F F F上的每个通道值拉伸成1*C的向量,然后与 W W WC*N进行矩阵乘法,再将得到的结果1*N划分为2*2*N/4,整个过程结束就得到通道数减少4倍,分辨率也扩大4倍的上采样结果。
举个例子F=16*16*32;一般的双线性插值法上采样–>R = 32*32*16,本文得到的R = 32*32*8
1.1.3 Adaptive softmax
用DUpsampling直接结合到encoder-decoder框架中会遇到优化问题,作者再原始的softmax中添加一个参数T,用以锐化/平滑化softmax: softmax ( z i ) = exp ( z i / T ) ∑ j exp ( z j / T ) \operatorname{softmax}\left(z_{i}\right)=\frac{\exp \left(z_{i} / T\right)}{\sum_{j} \exp \left(z_{j} / T\right)} softmax(zi)=∑jexp(zj/T)exp(zi/T)
1.1.4 Flexible Aggregation of Convolutional Features
早先的encoder-decoder中,为了预测高分辨率,通常是在decoder中结合通常是1/4初始分辨率特征和高分辨率的低级特征。
而如果在上采样过程中使用DUpsampling,则可以一直下采样直至得到最后的 F l a s t F_{last} Flast.并且在结合时,可以对下采样中的任意特征进行整合。F是产生预测结果的最终特征图,Fi代表中间层特征图,F_last代表最后一层卷积的特征图(encoder中)
F = f ( concat ( downsample ( F i ) , F last ) ) \mathbf{F}=f\left(\text { concat ( downsample }\left(\mathbf{F}_{i}\right), \mathbf{F}_{\text { last }}\right) ) F=f( concat ( downsample (Fi),F last ))
1.2 Experiments
1.2.1 DUpsampling与Bilinear
作者在PASCAL VOC的验证集上,将input_resolution/output_resolution设置为16和32测试,得到如下的实验结果:
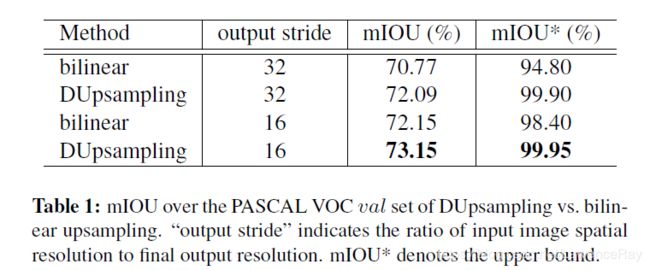
另外,作者测试了结合不同的层次的特征得到的性能也稍有差异,证明了确实在结合低层特征时的灵活性。[backbone=ResNet50]
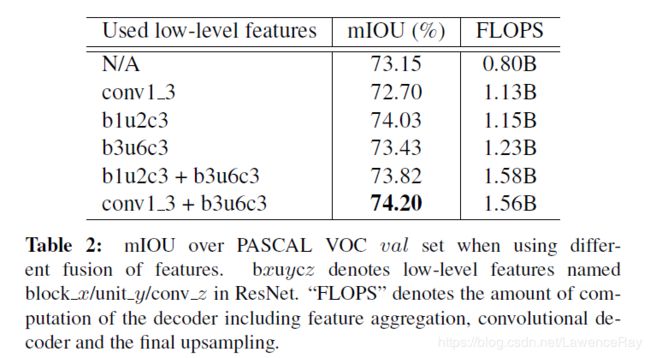
1.2.2 Comparison with the vanilla bilinear decoder
然后作者在PASCAL VOC上对ResNet-50和Xception-65进行实验,对比使用原始bilinear和DUpsampling的方法,后者均有不同幅度的提升。
另外作者还利用Xception-71作为backbone在Cityscapes上进行实验,但是bilinear的效果要稍微好一些:
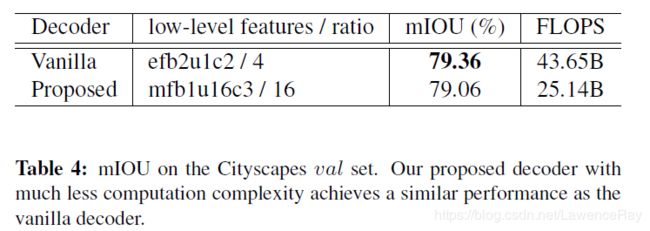
1.2.3 Impact of adaptive-temperature softmax
这一部分作者分析adaptive softmax的作用,使用原始的softamx的模型取得的结果只有%69.81远不如使用adaptive softmax的73.15%.作者给出结合不同的softmax模型训练过程中的loss曲线。
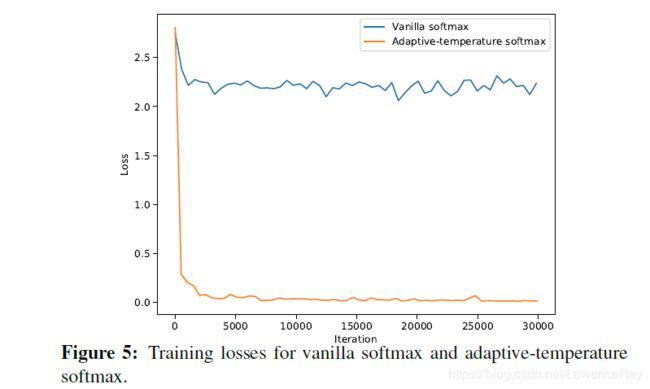
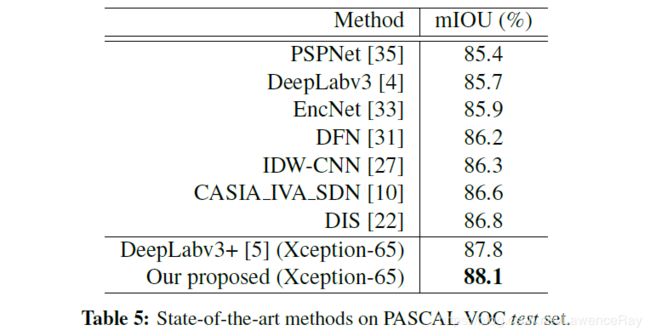
1.2.4 对比SOTA方法
然后作者在PASCAL VOC和·PASCAL Context上对比了一些SOTA方法的性能,如下: