2019杭电多校第二场

1005 Everything Is Generated In Equal Probability HDU-6595

/****************************
HDU 6595 杭电多校2019-2 1005

解题方法：通过样例逆元后的结果可以求出逆元前的期望，然后找(猜)到了规律 
 
**************************/
#include
using namespace std;
#define ll long long
ll mod = 998244353; //宏定义一个mod

ll quick_pow(ll a,ll b)
{
    ll ans=1;
    while(b){
        if(b&1) ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans;
}

ll inv(ll a,ll b)
{
    return (a*quick_pow(b,mod-2))%mod;
}

int main()
{
    ll n;
    while(cin>>n){
		cout<

 1008 Harmonious Army HDU-6598

/*****************************
HDU 6598 杭电多校2019-2 1008 
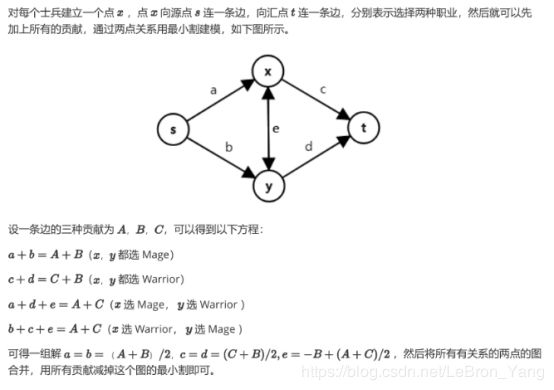
题意：有n个士兵，m对关系，分别有两个阵营，在每对关系中有u,v,A,B,C
如果士兵均属于战士加A点攻击，均属于法师加C点攻击，其他情况加B点攻击 
求士兵可以到达的最大攻击力 
思路：看了题解之后发现这个题目的建图非常巧妙，是一个两点式求最小割的题目
根据题解建好图之后，所有攻击力之和减去最小割即为士兵的最大攻击力值

关于建图：看着题解的建图真的看不懂为什么那么去建，但是你按照这个建好之后
你会发现这个图非常神奇，有四条最小割的方法分别对应三种羁绊值的加成，刚好
跑完所有情况 
 
*****************************/
#include 
using namespace std;
#define ll long long 
const int VM = 10000+7;
const int EM = 200000+7;
const int INF = 0x3f3f3f3f;

int deep[VM], dl[EM], to[EM],  fir[EM], nxt[EM] , uu[EM] , cnt, aim,xxx[EM];
double flow[EM];
void add(int u, int v, double w)
{
    to[cnt] = v;
    uu[cnt] = u;
    flow[cnt] = w;
    nxt[cnt] = fir[u];
    fir[u] = cnt++;
}

bool bfs(int S, int T)
{
    memset(deep, 0, sizeof deep);
    deep[S] = 1; dl[1] = S;
    int head = 0, tail = 1;
    while(head != tail)
    {
        int v = dl[++head];
        for(int u = fir[v]; u^-1; u = nxt[u]){
            if(flow[u] && !deep[to[u]])
            {
                deep[to[u]] = deep[v]+1;
                dl[++tail] = to[u];
            }
        }
    }
    return deep[T];
}

double dfs(int now, double fl)
{
    if(now == aim)return fl;
    double f = 0;
    for(int u = fir[now]; u^-1 && fl; u = nxt[u]){
        //xxx[now] = u;
        if(flow[u] && deep[to[u]] == deep[now]+1){
            double x = dfs(to[u], min(fl, flow[u]));
            flow[u] -= x;
            flow[u^1] += x;
            fl -= x;
            f += x;
        }
    }
    if(!f)deep[now] = -2;
    return f;
}

double maxflow(int S, int T)
{
    int nm=1;
    aim = T;
    double ans = 0;
    while(bfs(S, T)){
    	//for(int i = 0; i <= n; i++)xxx[i]=fir[i];
		ans += dfs(S, INF);
	}
    return ans;
}

int main()
{
    int n,m;
	while(~scanf("%d%d",&n,&m)){
		memset(fir,-1,sizeof fir);
    	cnt=0;
    	double sum=0;
    	while(m--){
    		int u,v;
    		double a,b,c;
    		scanf("%d%d%lf%lf%lf",&u,&v,&a,&b,&c);
    		add(0,u,(a+b)/2);
    		add(u,0,0);
    		add(0,v,(a+b)/2);
    		add(v,0,0);
    		add(u,n+1,(b+c)/2);
    		add(n+1,u,0);
    		add(v,n+1,(b+c)/2);
    		add(n+1,v,0);
    		add(u,v,-b+(a+c)/2);
    		add(v,u,-b+(a+c)/2);
    		sum+=(a+b+c);
		}
		printf("%lld\n",(ll)(sum-maxflow(0,n+1)));
	}
    return 0;
} 

 1009 I Love Palindrome String HDU-6599

/***************************
HDU 6599 杭电多校2019-2 1009 

题意：给你一个字符串，求所有长度的回文串有多少个
同时满足该回文串的一半也为回文串

思路：回文树求出cnt数组和len数组，即可得出符合第一个条件的情况
然后进入一个check，跟自己的父亲串作比较，看自己一半是否同时满足条件
满足条件加进ans数组，最后输出即可 
*********************************/
#include
using namespace std;
#define ll long long

const int maxn = 300005;
char str[maxn];

struct PAM
{
	int nxt[maxn][26],fail[maxn],len[maxn],cnt[maxn],S[maxn];
	int id,n,last;
	int newnode(int x)
	{
		for(int i=0;i<26;i++) nxt[id][i]=0;
		cnt[id]=0;
		len[id]=x;
		return id++;
	}
	void init()
	{
		id=0;
		newnode(0);
		newnode(-1);
		fail[0]=1;
		S[0]=-1;
		last=n=0;
	}
	int getfail(int x)
	{
		while(S[n-len[x]-1]!=S[n]) x=fail[x];
		return x;
	}
	void Insert(int c)
	{
		c-='a';
		S[++n]=c;
		int cur=getfail(last);
		if(!nxt[cur][c]){
			int now=newnode(len[cur]+2);
			fail[now]=nxt[getfail(fail[cur])][c];
			nxt[cur][c]=now;
		}
		last=nxt[cur][c];
		cnt[last]++;
	}
	void getsum()
	{
		for(int i=id-1;i>=0;i--){
			cnt[fail[i]]+=cnt[i];
		}
	}
}pam;

int ans[maxn];

bool check(int x)
{
	int t1=pam.len[pam.fail[x]];
	int t2=pam.len[x]-t1;
	if((pam.len[x]/2)%t2==0) return true;
	else return false;
}


int main()
{
	while(~scanf("%s",str)){
		pam.init();
		int len=strlen(str);
		for(int i=0;i<=len;i++) ans[i]=0;
		for(int i=0;i

1010 Just Skip The Problem HDU-6600

/**********************
HDU 6600 杭电多校2019-2 1010
题意：
给一个n。从0~pow(2,n)-1中选个数记为m。
你只可以问一次，但一次可以问多个数与m的按位与的答案是否和m相同。
问最少的数可以答案的方案有多少种。
思路：
假设我们问k个数。那么答案的组合一共是pow（2,k）种，
即我们可以用这k个数区分pow(2,k)个数。
所以如果我们想在0~pow(2,n)-1中区分出某个数，
则需要问log2（pow（2，n）-1+1）（==n）个数。
这要问的n个数全排列即是所有方案。
所以答案就是n!(设计取模问题)。
************************/
#include
using namespace std;
#define ll long long

const ll mod = 1e6+3;

ll f(ll n)
{
    ll ans=1;
    for(ll i=1;i<=n;i++) ans=(ans*i)%mod;
    return ans;
}

int main()
{
    ll n;
    while(cin>>n){
        if(n>=1e6+3) cout<<0<

1011 Keep On Everything But Triangle HDU-6601

/*****************************
HDU 6601 杭电多校2019-2 1011
题意：给定n和q，表示接下来有一个长度为n的数组输入，然后是q次询问，每次询问l，r表示求l到r间选三个元素表示边长组成的三角形周长最长，输出周长。
思路：主席树模板，求区间第k大数。从区间前三个开始遍历，如果组不成三角形就继续往后移（组不成三角形的条件是第三边大于等于其余两边之和），由于ai限定数据范围在1e9，根据斐波那契数最多用求区间前44个即可（斐波那契数求法就是前两个数之和，即三边组不成三角形的极限条件，44个斐波那契数之后就超出1e9范围），如果前44个没有找到就表示区间内组不成三角形。
*****************************/
#include
#define INF 0x3f3f3f3f
#define eps 1e-8
using namespace std;
#define ll long long
 
const ll MAXN = 100005;
const ll MAXM = 2000005;
 
vector ha;
ll a[MAXN];
ll tot;
 
struct NODE
{
    ll count;
    ll left, right;
};
 
ll root[MAXN];
NODE node[MAXM];
 
ll null;
 
ll newnode(ll count, ll left, ll right)
{
    node[tot].count=count;
    node[tot].left=left;
    node[tot].right=right;
    return tot++;
}
 
ll ins(ll rt, ll l, ll r, ll k)
{
    if (l <= k && k <= r)
    {
        if (l == r)
        {
            return newnode(node[rt].count + 1, 0, 0);
        }
        ll m = (l + r) >> 1;
        return newnode(node[rt].count + 1,
                       ins(node[rt].left, l, m, k),
                       ins(node[rt].right, m + 1, r, k));
    }
    return rt;
}
 
ll query(ll p, ll q, ll l, ll r, ll k)
{
    if (l == r)
    {
        return ha[l];
    }
    ll m = (l + r) >> 1;
    ll cot = node[node[q].left].count - node[node[p].left].count;
    if (cot >= k)
    {
        return query(node[p].left, node[q].left, l, m, k);
    }
    return query(node[p].right, node[q].right, m + 1, r, k - cot);
}
 
int main()
{
    ll n, q;
    while(~scanf("%lld%lld",&n,&q))
    {
        ha.clear();
        tot = 0;
        for(ll i = 1; i <= n; i ++)
        {
            scanf("%lld", &a[i]);
            ha.push_back(a[i]);
        }
        sort(ha.begin(), ha.end());
        ha.erase(unique(ha.begin(), ha.end()), ha.end());
        ll m = ha.size();
        null = newnode(0, 0, 0);
        root[0] = newnode(0, 0, 0);
        for(ll i = 1; i <= n; i ++)
        {
            a[i] = lower_bound(ha.begin(), ha.end(), a[i]) - ha.begin();
            root[i] = ins(root[i - 1], 0, m - 1, a[i]);
        }
        while(q--)
        {
            ll l, r, k;
            scanf("%lld%lld", &l, &r);
            ll xx,yy,zz,z=r-l+1;
            bool f=false;
            for(ll i=1;i<=r-l-1;i++){
                if(i==1) xx=query(root[l - 1], root[r], 0, m - 1, z-i+1),yy=query(root[l - 1], root[r], 0, m - 1, z-i),zz=query(root[l - 1], root[r], 0, m - 1, z-i-1);
                else xx=yy,yy=zz,zz=query(root[l - 1], root[r], 0, m - 1, z-i-1);
                if(yy+zz>xx){
                    f=true;
                    printf("%lld\n",xx+yy+zz);
                    break;
                }
            }
            if(!f) puts("-1");
        }
    }
    return 0;
}

1012 Longest Subarray HDU-6602

///*
HDU 6602 杭电多校2019-2 1012

题意：给出n，c，k。
接着给出n个数字（在1~c之间），问最长的区间长度。该区间满足任意一个出现的数字至少出现k次。

思路：
我们可以把可能满足条件的区间进行判断，
然后安区间内不符合条件的数的下标进行再次分区间，
再次进行判断。一直到所有的可能满足条件的区间都被判断完。

总结；
在分区间时，对于边界的处理比较繁琐，(l,r)与不满足条件的数的下标的关系要特别注意。
*///
#include
using namespace std;
#define met(a,b) memset(a,b,sizeof(a))
int a[100009];
int ans=0;
map >pos;
int n,c,k;
void dfs(int l,int r)
{
    if(r-l+1>n>>c>>k)
    {
        for(int i=1;i<=c;i++)pos[i].clear();
        met(a,0);
        ans=0;
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&a[i]);
            pos[a[i]].push_back(i);
        }
        dfs(1,n);
        cout<