CS231n课程作业(二) CNN

前言：

之前介绍了全连接网络(FC Net)，也就是常规的神经网络。

常规的神经网络是对input进行仿射变换、非线性变换等处理，最终计算出score。其目的是为了让input data所属类的score最高。为了达到这个目的，需要通过迭代不断地调整仿射变换时的参数W。(因此主要涉及的参数量也与W有关)

常规的神经网络表现还不错，但如果图像尺寸较大，则会出现问题：

我们之前数据集中图片尺寸为32x32x3，这样，在input layer 与第一个hidden layer之间，hidden layer中每一个神经元将会有3072个weights，W(3072, hidden_dim)。因此，如果图片尺寸较大，weight的数量也会剧增，处理起来将会很复杂。而且参数量过多会导致过拟合。So,为了解决这个问题，CNN牛逼起来了。因为CNN：局部连接、权值共享 。

一、CNN

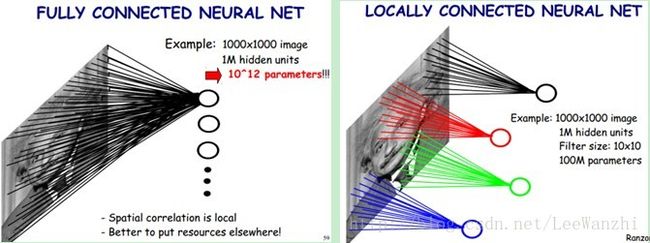
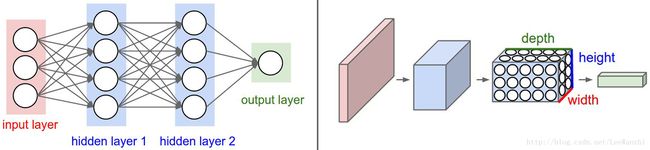
通过上图，可以发现全连接层每个神经元都与图片上所有像素相连接，而CNN则是局部连接。
注：由于FC网络输入的是向量，而CNN输入的是图像，因此图2 在表示上有很大的不同。但CNN进入FC layer时，仍然会将input data reshape为(N,D)

局部连接： 每个神经元只与上一层中的局部区域相连接，局部连接的空间大小称为局部感受野。

假设，每个神经元连接F x F个像素区域，则W参数个数为hidden_dim * F * F。这意味着，局部连接可以使参数数目锐减。

关于局部连接，其实人分辨事物也是这样，不是直接看到一个东西就知道它是什么，而是先感知局部信息，然后将局部信息综合起来得到全局信息。

权值共享： 当前层每个神经元都使用相同的W和bias。

这个需要继续上面的局部连接，在局部连接中，每个神经元只是连接的像素数锐减了，但没有说因此关联的W相同。在权值共享中，则进一步显示CNN的优点，那就是所有神经元使用的W都相同，参数个数不再与神经元个数有关。这样参数量为F * F (注：这里暂时忽略3 channels以及bias)。参数真的是锐减啊！

CNN的框架：

和FC神经网络一样，CNN没有固定的框架。但一般都会有Conv Layer、ReLU Layer、Pooling layer、FC layer这些结构。下面详细阐述。

二、Conv Layer (卷积层)

1. 卷积层的相关计算

卷积层的工作：利用卷积核或者称为滤波器对input图像做卷积运算。
将卷积核与对应区域相乘，再全部相加(包括所有通道)。

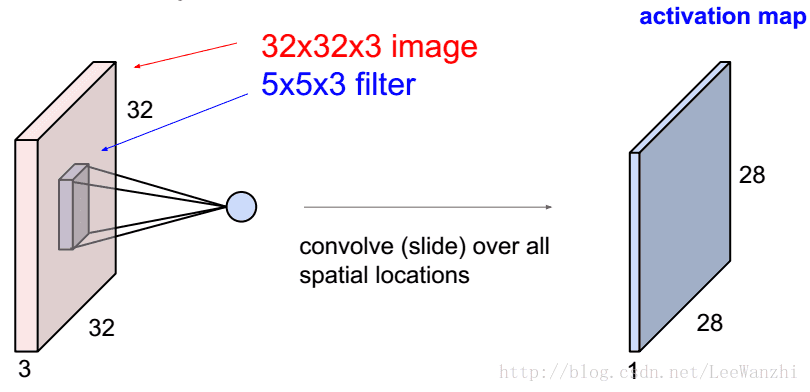
图中为1个filter，如果我们有6个，则可以得到28 x 28 x 6 的feature map。
参数量为： (5 * 5 * 3 + 1)*6
具体为什么feature map是这样的size，其实自己移一移filter就知道了，下面给出计算公式。

注：卷积核的深度总是和输入图像的深度相等。

假设input size：W1 x H1 x D1
此时，需要4个hyperparameters:
number of filters K ; filter spatial extent F ; stride S ; the amount of zero-padding: P

then the output size: W2 x H2 x D2, where:

W2 = (W1 - F + 2P)/S + 1

H2 = (H1 - F + 2P)/S + 1

D2 = K

由于权值共享，因此每个filter产生F * F * D1个weights，一共产生(F * F * D1)*K个weights和K个bias。(K通常为2的指数，据说会让PC进入高效率运算)

注：In practice, common to zero-pad the border: (F-1)/2。
这样尺寸就不会改变，毕竟不能抢了池化层的饭碗。

2. 如何理解卷积层

卷积层的训练实际是训练不同的filters，每个filter都可以对特定的模式进行激活，即对于特定的模式输出值很高，对于其他模式输出值很低。

如图，展示的是不同模式的filter，它们只激活特定的模式。(这篇paper可以看一看)

CNN的第一个卷积层用来检测low level feature，比如边、角、曲线等，然后将输出的feature map(activation map)传递至第二层。随着卷积层的增加，filter检测的feature就越来越复杂。如第二层filter用于检测low level feature的组合，如半圆、四边形等。

在初始化时，filter的权值都是random的，它们无法检测任何feature。此时，它们需要被告知what the object is，然后学习这些特征，使损失函数最小。这个过程就叫做训练。

关于卷积层的工作，可以结合下图感受一下：

其中，亮色的value很高，黑色的value很低且为负值，背景色的value在0左右。可以看出卷积层先是对low level feature有较高的输出，逐渐地对low level feature的组合，即high level feature有很高的输出(即该类别最独特的特征)，最终进入FC层进行分类。

交互式界面链接在此：卷积神经网络交互式界面

三、Pooling layer(池化层)

卷积运算时通常不改变图片的空间尺寸，空间尺寸的减小通常在池化层中进行。在实际应用中，一般都将图像尺寸减半。
因此，常用设置 [filter: 2x2 ; stride :2]

分类：
max pooling：最大池化，依次将filter在input image上滑动，取区域中的最大值
average pooling：平均池化，依次将filter在input image上滑动，取区域中的平均值

计算输出尺寸：
假设输入尺寸: W1 x H1 x D1
需要两个hyperparameters：
filter的尺寸 F， 步长 S

输出尺寸为： W2 x H2 x D2， where:

W2 = (W1 - F)/S + 1

H2 = (H1 - F)/S + 1

D2 = D1

注意：池化层中不使用zero-padding
Attention：池化层中没有参数，因为要么是最大池化，要么是平均池化，不需要参数。卷积层中有。

四、本次作业中的CNN

本次作业是一个3-layer CNN，结构可以表示为：

input - [Conv - ReLU - max pool] - [FC - ReLU] - [FC - Softmax]

首先是构建好这个框架model，然后定义一个solver对model进行训练，得到best model。即可进行predict。

model = ThreeLayerConvNet(weight_scale=0.001, hidden_dim=500, reg=0.001)

solver = Solver(model, data,
                num_epochs=1, batch_size=50,
                update_rule='adam',
                optim_config={
                  'learning_rate': 1e-3,
                },
                verbose=True, print_every=20)
solver.train()

五、spatial batch normalization(空间批量归一化)

在FC网络中，BN对结果有很大的改善。但在CNN中，实际上经过多次实验表明，有BN和没有BN其实没有什么区别，所以CNN现在一般不用BN了。但为了知识的全面性，还是要提一下。

在FC网络中，input是(N,D),我们是在D方向上求均值和方差，即对矩阵每一列分别求均值和方差。

在CNN中，由于input(N,C,H,W)，我们reshape input为(N*H*W, C)，在深度方向上对每个通道进行均值和方差的计算，然后再进行归一化、缩放平移。最后再将input数据 reshape回来。

其余操作和FC网络一样。

六、python知识补充

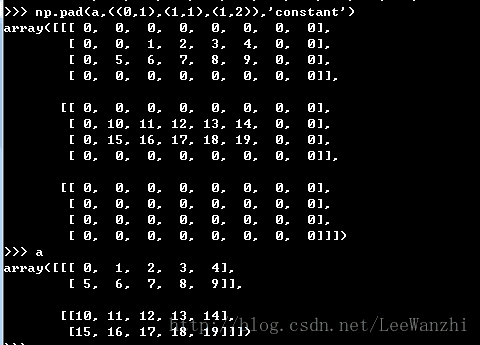
1. np.pad(array,tuple,’constant’, [constant_value = 0])
function: zero-padding
tuple内有几个元组即对几个维度操作，(0,0)表示不填充，(1,1)表示填充上下或左右各一个元素
eg: