PRML读书笔记(一)

Machine Learning 基础

Machine Learning 步骤

整个机器学习大致可以分为4个步骤：数据分析，数据预处理，模型选择以及训练和优化。比较宏观的流程如下图所示。

栗子：Polynomial Curve Fitting

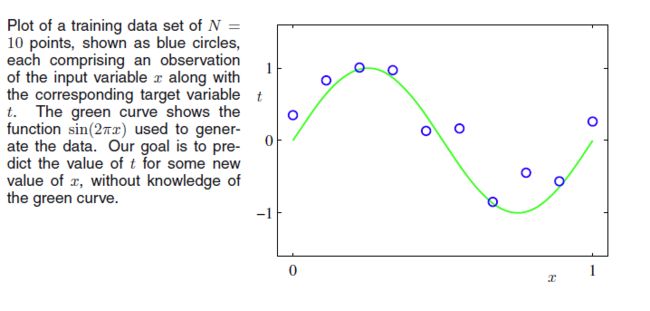
假设我们现在有一组从 f(x)=sin(2πx)+ϵ(x) 生成的数据，其中 ϵ(x)=N(x|0,β) 表示噪声。那么我们就得到原始数据为

x=(x1,x2,…,xN)T,xi∈(0,1) ，相对应的函数值 t=(t1,t2,…,tN)T 。我们要预测，一个新的数据 x~ 相对应的函数值。

我们得到的只有 x,t ，并不知道 f(x) 的形式。

数据分析(Data Analysis)

由于训练数据由输入向量与其对应的输出向量组成，因此这是一个监督学习(supervised learning)的问题，并且由于输出向量是一组连续的变量，故又可以细分成回归问题(regression)。那么我们可以用以下函数取逼近

y(x,w)=w0+w1x+w2x2+⋯+wMxM=∑Mj=0wjxj(1)

理论

数据预处理(Preprocess)

数据预处理具有以后优点：
1. 减小输入的多变性，比如输入数据是一系列图片时，我们可能需要将这些图片转换成固定尺寸的图片
2. 加速计算，例如归一化处理，能够输入向量转换到均值为0的特征空间，从而减小划分曲面的偏置搜索
3. 其他

在curve fitting中，我们需要将输入向量转换成 X=⎡⎣⎢⎢⎢⎢⎢11⋮1x10x11⋮x1N……⋱…xM0xM1⋮xMN⎤⎦⎥⎥⎥⎥⎥

如果是在训练的时候计算 xji 的话，会消耗大量的计算资源。

模型选择

损失函数

由数据分析步骤，我们已经得到了基础的模型，我们希望我们的预测值 y(x,w) 与 t 尽量相近，那么我们可以用以下度量来表示

L(y,t)={y(x,w)−t}2(2)

那么对于整体训练数据的度量就可以由(2)得到，

E(w)=∫x×tP(x,t)L(y(x,w),t)dxdt(3)

上式(3)在本例中可以等价于

E(w)=1N∑n=1NL(y,t)(4)

需要注意的是公式(3)与公式(4)表达的意思并不是一样的，式(3)是期望风险(模型关于联合分布的期望损失)，式(4)是经验风险(模型关于训练样本的平均损失)，当 P(x,t)=1N 或者样本容量N趋向于无穷时，经验风险趋向于期望风险。

超参数

式(1)里的参数M是不能在训练中直接学到的，需要在训练之前设置，因此称为超参数(hyperparameter)，一个方法是令 M=1,2,3,… ，但是在经验风险下 E(w)=12∑Nn=1L(y(x,w),t) ，M的不同会使模型的较大的性能差；另一个方法是采用正则化方法

E~(w)=12∑n=1NL(y(x,w),t)+λ2||w||2(5)

之后会详细介绍这两种损失函数的概率意义。

训练与优化

在本例中可以用最小二乘法，直接求解。

实验结果

E(W)下的结果

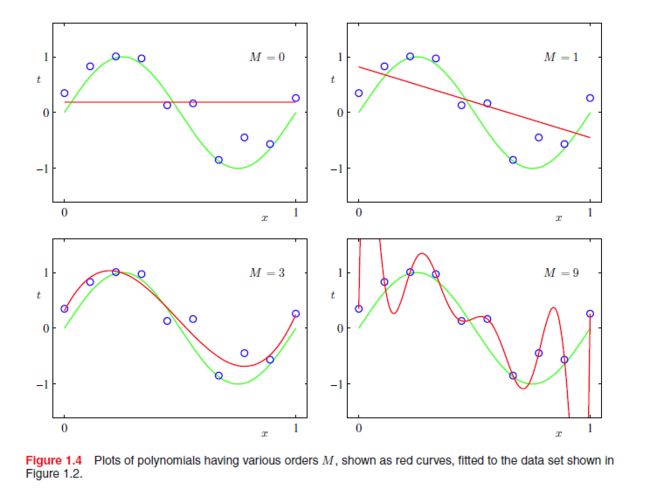
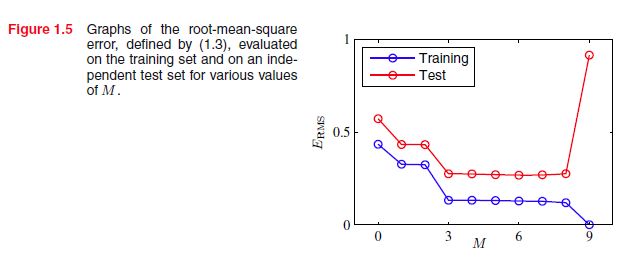
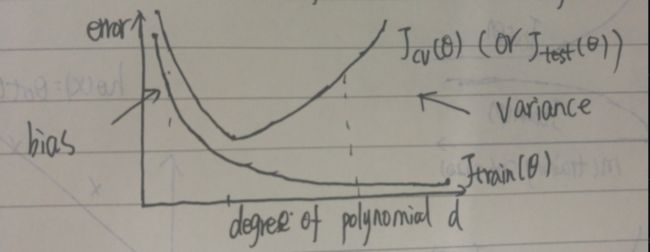
我们可以从上图看到，当 M=0,1,3,9 的时候，随着M的增加，曲线能很好更好的拟合训练数据，在 M=9 的时候 E(W)=0 ，但是很明显如果来了一个新的测试数据， M=3 的效果是最好的，这是因为 M=0,1 时，曲线处于欠拟合(underfitting)的状态，而 M=9 时则过拟合(overfitting)。

直觉上，我们认为 M=9 的模型会比 M<9 的模型要好，至少 M=9 的模型的性能不会低于 M<9 的模型，因为 M=9 的模型可以产生 M<9 的特殊子集(如 M=3 时 令 wi=0,i=4,…,9 )。下表是相应的权值 w∗ 。*

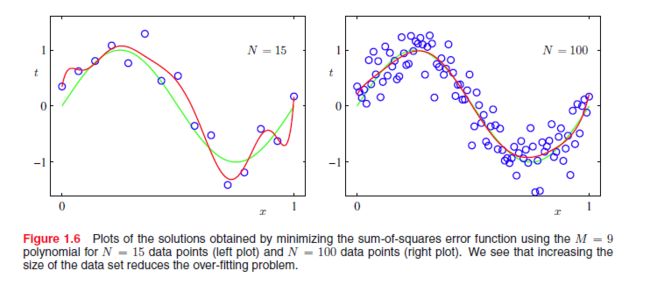
我们可以看到，随着M的增加，其相应的权值也会变得非常大。但是由于训练数据存在噪声，从而使整个曲线的震荡幅度变大。数据量越大，噪声的影响就越小。

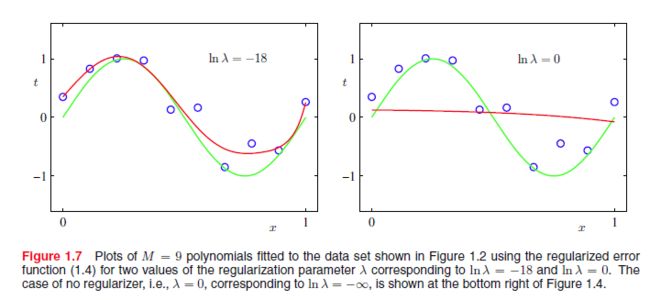
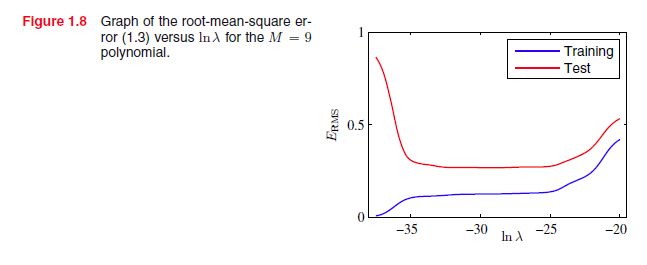
E~(W) 下的结果

由上述三图可以知道，在 E~(W) 的情况下，模型能够达到相当好的效果，这是因为正则项能够使权值收缩。从而能够降低噪声造成的震荡幅度。

损失函数

损失函数的概率意义

最大似然

对于训练样本 (x,t) ，我们希望 p(t|x,w)=∏Ni=1N(ti|y(xi,w),β) 达到最大，那么等价于

lnp(t|x,w)=−N2ln2π+N2lnβ−β2∑n=1N{y(xn,w)−tn}2(6)

即最小化 E(W) 等价于最大化 lnp(t|x,w) ，即 E(W) 具有最大似然的性质。

最大后验

前面的假设是对于任意的 w 具有相同的选择概率，但是如果我们引入先验知识，即

p(w|α)=N(w|0,α−1I)(7)

那么 p(t,w|x) 最大，由于 p(t) 可以看作一个常数，那么 p(t,w|x) 就等价于

p(w|x,t,α,β)∝p(t|x,β)p(w|α)(8)

ln{p(t|x,β)p(w|α)}=−N2ln2π+N2lnβ−β2∑n=1N{y(xn,w)−tn}2−N2ln2π+N2lnα−α2||w||2(9)

即等价于最小化 β2∑Nn=1{y(xn,w)−tn}2+α2||w||2 ，也就是最小化 E~(W) 等价于最大化后验概率。

bias和variance

E(L)=∫∫L(y(x),t)p(x,t)dxdt=∫∫{y(x)−t}2p(x,t)dxdt(10)

求极值

∂E(L)∂y(x)=2∫{y(x)−t}p(x,t)dt=0(11)

那么得到

y(x)=∫tp(x,t)dtp(x)=Et[t|x]

令

{y(x)−t}2={y(x)−E[t|x]+E[t|x]−t}2={y(x)−E[t|x]}2+2{y(x)−E[t|x]}2{E[t|x]−t}+{t−E[t|x]}2(12)

将式(12)代入到式(10)，可得到

E(L)=∫{y(x)−E[t|x]}2p(x)dx+∫{t−E[t|x]}2p(x,t)dxdt(13)

式(13)中的第一项可以表示为bias，第二项可以表示为variance， E(L)=bias+variance ，在polynomial curve fitting中，损失函数只优化了bias项，而variance项则相当于固定误差(对于特定的M)。在其他例子中，我们可以看到，函数的优化相当于trade-off between bias and variance。

第二项与 y(x) 无关，是数据的噪声的固定误差，即不管怎么优化， E(L)≥∫{t−E[t|x]}2p(x,t)dxdt 。第三章会详细介绍第一项的意义。