PRML读书笔记(四)

分类的线性模型

分类的目标是在给定输入，预测具有离散性质的目标值。输入空间被多个决策平面划分成多个决策区域，每个区域代表一个类别。决策平面是输入特征的线性函数(待会会详细介绍)，因此在D维空间上的决策平面是(D-1)维的超平面，如果数据能够被这些决策平面准确划分成n个类别区域，那么数据集线性可分(linearly separable)。

当有K(>2)类时，我们采用 1-of-K 编码格式也叫one-hot encoding。 t={0,…,1,…,0}T,∑ktk=1 。

生成模型与判别模型

这章的模型可以一般表示为

y(x)=f(wTϕ(x)+w0)

其中 f(⋅) 是激活函数。如果令 f 为一个恒等函数(identity function)，即 f(⋅)=⋅ ，那么这个模型就变成了第三章的线性回归模型；而如果 f 是非线性函数，那么这个模型就为分类模型，是一个广义线性模型(Generalized Linear Model,GLM)，这是因为决策平面为 y(x)=constant⇒wTϕ(x)+w0=constant ，可以看到决策平面是输入特征的线性函数。

4.1 判别函数(Discriminant Functions)

在给定输入特征时，判别函数输出一个类别 Ck

4.1.1 二分类问题

最简单的判别函数为如下的线性判别函数

y(x)=wTx+w0

当 y(x)≥0 时，我们将 x 分到类别 C1 ，否则分到 C2 。因此bias项 w0 的负值有时候也被称为阈值。

因此决策平面 S 就并定义成了 y(x)=0 ，从几何上看，我们可以知道 wT 是 S 的法线，那么 w0 就可就决定了决策平面与原点的距离 −w0∥w∥ 。

上图中 x 是空间上任意一点， x⊥ 是 x 正交投影到平面 S 上的点， r 是 x 到 S 的距离，那么

xr==x⊥+rw∥w∥y(x)∥w∥

如果令 x0=1,w~={w0,w},x~={x0,x} ，那么 y(x)=w~Tx~

4.1.2 多类别

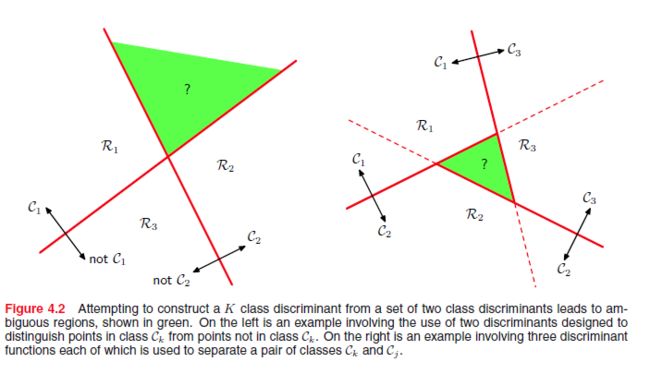
对于多类别，可以训练K-1个分类器，每个分类器可以看做是一个二分类问题，即类别 Ck 与 非 Ck ，由于约束，我们训练K-1个分类器即可；训练 K(K−1)/2 个分类器，类别为 Ck 和 Cj 。这两种方法都会导致模糊区域的问题

为了解决模糊区域问题，可以考虑 K 类别判别(K-class discriminant)，

yk(x)=wTkx+wk0

虽然形式上有点类似前两种方法，但是只有当所有 j≠k,yk(x)>yj(x) 时，才分类到 Ck ，那么 Ck 与 Cj 的决策边界(平面) 就变成了 yk(x)=yj(x)⇒(wk−wj)Tx+(wk0−wj0)=0 ，这与二分类的决策平面一致。

由上图知道 xa,xb 是决策区域 Rk 的任意两个点，那么在直线 xaxb 上的任一点 x^ ，我们可以表示为

x^yk(x^)==λxa+(1−λ)xb,0≤λ≤1λyk(xa)+(1−λ)yk(xb)

明显对于任意 j≠k ，我们有 yk(x^)≥yj(x^) ，即对于线性可分的数据， Rk 是单连通凸区域(singly connected and convex)。

4.1.3 分类的最小二乘法

采用最小二乘法能够使预测值逼近 E[t|x] ，详细参考第三章中的最小二乘法的解释。 对于K类别，我们有

y(x)ED(W~)⇒W~===W~Tx~12Tr{(X~W~−T)T(X~W~−T)}(X~X~)−1X~TT

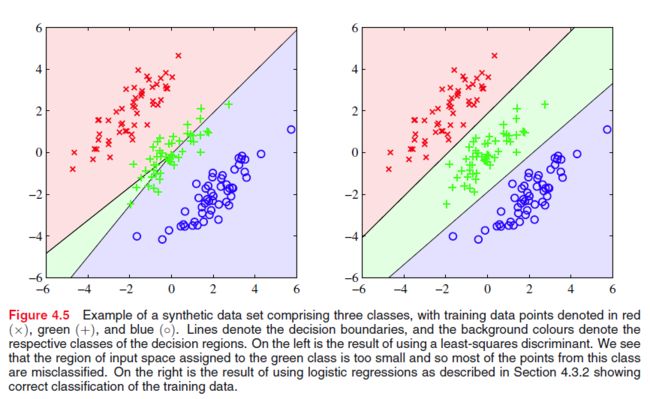
最小二乘法对离群点不鲁棒，如下图

左图的决策边界已经能够很好地划分两个区域了，但是来了一些新的数据的时候，如右图，尽管原先的决策边界也能够很好地划分数据，但是由于采用了最小二乘法，为了使损失达到最小，即划分边界距离两个类的条件期望 E[t|x] 最近，从而驱使原先的决策边界偏离，即右图紫色边界线。

(书上原话: The sum-of-squares error functin penalizes predictions that are ‘too correct’ in that they lie a long way on the correct side of descision boundary.)

我认为导致左图的原因除了二乘法原因外，还有 K-class discriminant方法中，所有的决策区域必定相交于一个平面，所以左图的数据对于 K-class discriminant是不可分的(?)

导致上述问题的一个根本原因是，最小二乘法是高斯分布假设下的最大似然估计解决方案，而对于分类问题的目标值是离散的，而不是连续的，从而与高斯分布假设不相符。

4.1.4 Fisher线性判别(Fisher’s linear discriminant)

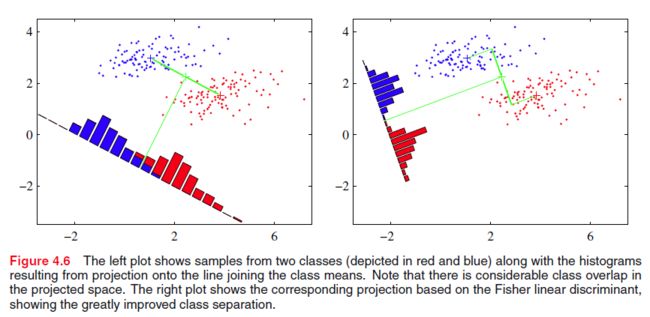
线性判别函数一般表示为 y=wTx ， 从几何上看，我们将 D 为输入 x 经过一个变换之后，输出了一个一维的空间 y ，并且在这个一维空间上不同类的数据是可分的。考虑2分类问题，只有推广。如果将每个类看成一个簇，那么它中点看做

m1=1N1∑n∈C1xn,m2=1N2∑n∈C2xn

为了使不同类的数据分开，我们使 m1,m2 投影到一维空间上的距离最远，即

m2−m1=wT(m2−m1)

假设 xa∈C1 ，当 xa 在 m1 附近或者 m1xa−→−− 的方向与 m1m2−→−−− 背离(夹角大于90度)，那么 xa 能够与 C2 中的点很好地分离，同理 C2 。
但是对于 xa 不在 m1 附近并且 m1xa−→−− 的方向与 m1m2−→−−− 同向(不是夹角等于0，而是夹角小于90度) ，那么这些点就有可能不能很好地分离开，如下图左图所示

Fisher linear discriminant wiki。Fisher线性判别对这个问题进行了研究，他的思想要使类内(within-class)数据的方差最小，并且使类间(between-class)数据的方差最大，从而得出了Fisher criterion

J(w)s2k==(m2−m1)2s21+s22∑n∈Ck(yn−mk)2

经过调整后，我们就得到了上图右图，可以看出此时不同类的数据已经能够很好地划分开来。

求解 w

J(w)SBSW⇒∂J∂w=0(wTSBw)SWw⇒w====∝wTSBwwTSWw(m2−m1)(m2−m1)T∑n∈C1(xn−m1)(xn−m1)T+∑n∈C2(xn−m2)(xn−m2)TSBw(wTSWw)S−1W(m2−m1)

需要注意的是此时求解的 w 是决策超平面的法向量，还需要选取一个阈值 y0 。

4.1.5 Fisher判别与最小二乘法的关系

最小二乘法：驱使模型的预测值与目标值尽可能相近

Fisher判别：最大化输出空间的类别差别

在二分类问题中，Fisher判别可以当做最小二乘法的一个特殊情况。在最小二乘法中，当我们用 {N/N1,−N/N2} 代替 {1,0} 时，即可得到Fisher判别。

4.1.6 多类别的Fisher判别

采用K-class discriminant模型，我们有

y=WTx

类比二分类的Fisher判别，我们有

mkSkmSBSWJ(W)======1Nk∑n∈Ckxn∑n∈Ck(xn−mk)(xn−mk)T1N∑nxn=1N∑k=1KNkmk∑k=1KNk(mk−m)(mk−m)T∑k=1KSkTr{(WSWWT)−1(WSBWT)}

4.1.7 感知器算法

感知器算法中与前两种方法不同的是采用了step激活函数

y(x)f(a)==f(wTϕ(x)){+1,a≥0−1,a<0

其中 ϕ0(x)=1 ，而且跟前面的方法目标值的表达不同 t∈{−1,+1} ，而不是 t∈{0,1} ，若 x∈C1,t=+1 ，否则 t=−1 。因此对于分类正确的数据 (xn,tn),yntn>0 ，对于误分的数据 yntn<0 ，所以感知器算法的损失函数就采用了

E(w)=−∑n∈MwTϕ(xn)tn

M 是误分的集合，采用随机梯度下降法对上述损失函数求解。

需要注意的是感知器只适用于二分类问题，而且当数据是非线性可分时，迭代不收敛；而且就算对于线性可分的数据，由于每一次迭代都会更改权值，从而影响先前的数据，使原本分类正确的数据在下一轮分类错误，迭代次数增大(当然最后是肯定收敛的)。因此在训练的时候，我们不知道数据到底是非线性可分还是迭代次数不够。

4.2 概率生成模型(Probabilistic Genertive Models)

首先对 p(x|Ck),p(Ck) 建模，然后根据贝叶斯定理计算 p(Ck|x) ，对于二分类问题

p(C1|x)a===p(x|C1)p(C1)p(x|C1)p(C1)+p(x|C2)p(C2)11+exp(−a)lnp(x|C1)p(C1)p(x|C2)p(C2)

对于多类别问题

p(Ck|x)ak===p(x|Ck)p(Ck)∑jp(x|Cj)p(Cj)exp(ak)∑jexp(aj)lnp(x|Ck)p(Ck)

4.2.1 连续型特征

对于连续型变量，我们可以假设似然函数服从高斯分布，并且所有的类别具有相同的协方差矩阵

p(x|Ck)=N(x|μk,Σ)

对于二分类问题，则有

p(C1|x)ww0===σ(wTx+w0)Σ−1(μ1−μ2)−12μT1Σ−1μ1+12μT2Σ−1μ2+lnp(C1)p(C2)

由上面的推导我们知道，先验概率只出现在bias项，因此改变先验会影响决策平面的偏移。

对于一般K类，则有

ak(x)wkwk0===wTkx+wk0Σ−1μk−12μTkΣ−1μk+lnp(Ck)

上述推导都可以通过贝叶斯定理与替换推出。

4.2.2 最大似然方案

对于二分类问题，假设我们有训练数据 {xn,tn},n=1,…,N ，当 xn∈C1,tn=1;xn∈C2,tn=0，p(C1)=π,p(C2)=1−π 。那么

p(xn,C1)p(xn,C20)⇒p(t|π,μ1,μ2,Σ)===∝p(C1)p(xn|C1)=πN(x|μ1,Σ)p(C2)p(xn|C2)=(1−π)N(x|μ2,Σ)∏n=1N[p(C1|xn)]tn[p(C2|xn)]1−tn∏n=1N[πN(x|μ1,Σ)]tn[(1−π)N(x|μ2,Σ)]1−tn

为了方便，我们令 p(t|π,μ1,μ2,Σ)=∏Nn=1[πN(x|μ1,Σ)]tn[(1−π)N(x|μ2,Σ)]1−tn ，根据 π,μ1,μ2 求其偏导为0的解

πμ1μ2ΣSk=====N1N1+N21N1∑n∈C1xn=1N1∑n=1Ntnxn1N2∑n=1N(1−tn)xnN1NS1+N2NS21Nk∑n∈Ck(xn−μk)(xn−μk)T

4.2.3 离散型特征

假设输入特征为离散型，我们考虑 xi∈{0,1} 的情况，对于D维的特征向量，我们假设每一维特征都相互独立，则有

p(x|Ck)ak===∏j=1Dμxjkj(1−μkj)1−xjlnp(x|Ck)p(Ck)∑j=1D{xjlnμkj+(1−xj)ln(1−μkj)}

采用最大似然估计的分析跟连续型特征的类似，所以不再复述。

4.2.4 指数族

由第二章我们知道高斯分布与伯努利分布都可以划分到指数族中，现在我们泛化

p(x|λk)=h(x)g(λk)exp(λku(x))

如果我们令 u(x)=x ，并且再对 x 缩放，那么

p(x|λk,s)ak(x)==1sh(1sx)g(λk)exp(1sλku(x))λTkx+lng(λk)+lnp(Ck)

4.3 概率判别模型

在上一节中我们引入了 ak(x) 在生成模型中好像有点多余，那是因为是为了给概率判别模型做铺垫。在生成模型中，我们必须先要对 p(x|Ck),p(Ck) 建模才能得到后验概率，而我们已经知道 y(x)=f(wTϕ(x)) 是一个广义的线性模型，并且如果选择一个特殊的激活函数，如sigmoid、softmax，会得到后验概率，从而我们希望直接定义 p(Ck|x) 的函数来求解。概率判别模型的一个有点是参数少。

4.3.1 基函数

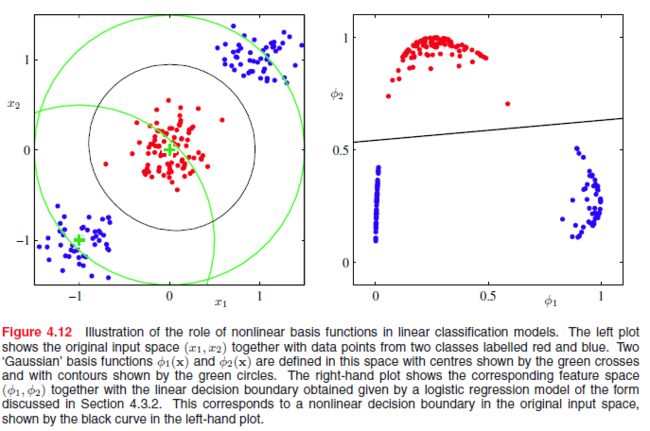
上面讨论的时候，我们都是考虑原始空间上的分类问题，但是在原始空间上的数据可能非线性可分的，但是如果我们经过一个非线性基函数变换后，在变换的空间上，数据是线性可分的。如下图所示

在实际问题中，类别条件密度 p(x|Ck) 会有重叠，因此相应的 p(Ck|x) 有一些 (0,1) 区间的模糊集，这时需要采用decision theory。需要注意的是，非线性变换并不能解决这个问题，甚至有可能引入新的重叠，但是合适的基函数能够使后验概率的建模过程更加简单。

4.3.2 逻辑斯蒂回归(Logistic Regression)

对于二分类问题，上一小节我们推导出

p(C1|x)σ(a)==y(x)=σ(wTϕ)11+exp(−a)

那么 p(C2|x)=1−p(C1|x)

假设 ϕ 的维度是M，那么这个模型的参数只需要M个。而对于生成模型，则需要 2M+M(M+1)/2=M(M+5)/2 个参数。

对于训练集 {ϕn,tn},tn∈{0,1},ϕn=ϕ(xn),n=1,…,N ，那么似然函数为

p(t|w)E(w)==∏n=1Nytnn{1−yn}1−tn−lnp(t|w)=−∑n=1N{tnlnyn+(1−tn)ln(1−yn)}

上式中的 yn=σ(wTϕn) ， E(w) 称为交叉熵损失函数。

∇E(w)=∑n=1N(yn−tn)ϕn

可以采用随机梯度下降求解。

关于最大似然导致严重过拟合的原因没看明白(todo)

4.3.3 迭代再加权最小二乘(iterative reweighted least square)

由于sigmoid函数， ∇E(w) 不再具有闭式解(closed-form solution)。但是它还是一个凸函数，因此具有一个全局最小解，可以采用Newton-Raphson法来求解

wτ+1=wτ−H∇E(w)

在线性回归中

∇E(w)H⇒wτ+1===∑n=1N(wTϕn−tn)ϕn=ΦTΦw−ΦTt∇∇E(w)=ΦTΦwτ−H∇E(w)=(ΦTΦ)−1ΦTt

我们可以看出标准最小二乘法与Newton-Raphson法得到相同的解。

对于logistics回归模型

∇E(w)HR===∑n=1N(yn−tn)ϕn=ΦT(y−t)∇∇E(w)=∑n=1Nyn(1−yn)ϕnϕTn=ΦTRΦdialog{yn(1−yn)}

由于 0<yn<1 ，那么对于任意向量 u,uTRu>0 ，即 R 是正定矩阵。所以 E(w) 是一个凸函数。用Newton-Raphson法对logistics模型求解得

wτ+1z===wτ−(ΦTRΦ)−1ΦT(y−t)(ΦTRΦ)−1ΦTRzΦwτ−R−1(y−t)

因为 R 不是常数，而依赖于 w ，因此我们需要用上式迭代求解。 R 可以看做是方差。

4.3.4 多类别逻辑斯蒂回归

4.2小节我们推导出，K分类的一般形式为

p(Ck|ϕ)ak∂yk∂aj===yk(ϕ)=exp(ak)∑jexp(aj)wTϕyk(Ikj−yj)

那么似然函数为

p(T|w1,…,wK)E(w1,…,wK)==∏n=1N∏k=1Kp(Ck|ϕn)tnk−lnp(T|w1,…,wK)=−∑n=1N∑k=1Ktnklnynk

其中 ynk=yk(ϕn) ，那么

∇wjE(w1,…,wK)=∑n=1N(ynj−tnj)ϕn

我们可以采用随机梯度下降求解 wτ+1k=wτk−η∇wkE(w1,…,wK) ，或者考虑IRLS

∇wk∇wjE(w1,…,wK)=−∑n=1Nynk(Ikj−ynj)ϕnϕTn

4.3.5 Probit Regression

前面我们考虑的激活函数都是logistics或者softmax函数，现在我们考虑其他的激活函数 p(t|a)=f(a) ，当 a>θ,tn=1 ，那么 θ 的任意概率密度 p(θ) ，我们得到

f(a)=∫a−∞p(θ)dθ

当我们假设 p(θ)=N(θ|0,1) 时，我们有 Φ(a)=∫a−∞N(θ|0,1)dθ ， Φ(a) 就被称为probit函数。

erf(a)Φ==2π√∫a0exp(−θ2/2)dθ12{1+12√erf(a)}

之后的求解过程与logistics模型一致，但是需要注意的是probit模型比logistics模型对离群点更敏感。

4.3.6 Canonical link functions

4.4 拉普拉斯逼近(The Laplace Approximation)

在线性回归的时候我们讨论了贝叶斯分析的形式如下

p(t|t,α,β)=∫p(t|w,β)p(w|t,α,β)dw

但是在logistics回归中，后验概率不再是高斯分布函数，因此我们希望能够寻求一个高斯分布来近似后验分布。

对于任意一个分布，我们有

p(z)=1Zf(z),Z=∫f(z)dz

Laplace逼近的目标就是找到一个高斯函数 q(z) ，使其均值为 p(z) 的模。第一步是找到模 z0 ，由于高斯分布的对数是变量的二项式函数，那么 lnf(z) 在 z0 附近的泰勒展开式如下

lnf(z)A⇒f(z)⇒q(z)≃=≃=lnf(z0)−12A(z−z0)2−d2dz2lnf(z)∣∣z=z0f(z0)exp{−A2(z−z0)2}(A2π)1/2exp{−A2(z−z0)2}

同理对于M为变量也是如此求解

lnf(z)A⇒f(z)⇒q(z)≃=≃=lnf(z0)−12(z−z0)TA(z−z0)−d2dz2lnf(z)∣∣z=z0f(z0)exp{−12(z−z0)TA(z−z0)}|A|1/2(2π)M/2exp{−12(z−z0)TA(z−z0)}

laplace逼近只适用于实数变量。当数据集很大时，Laplace逼近有很好地效果。

4.4.1 模型比较

对于模型 Mi 有参数集 {θi} ，那么这个模型的model evidence为

p(D)lnp(D)==∫p(D|θ)p(θ)dθlnp(D|θMAP)+lnp(θ)+M2ln2π−12lnA

如果我们假设高斯先验概率的参数是平(broad)的话，那么

lnp(D)=lnp(D|θMAP