Simultaneous Deep Transfer Across Domains and Tasks 域和任务同时深度迁移
论文地址:https://people.eecs.berkeley.edu/~jhoffman/papers/Tzeng_ICCV2015.pdf
现有的迁移学习方法很多都只做了一步:域适应,也就是减少边缘概率(marginal distribution)差异----使两个域尽可能重叠、融合,但是当边缘分布得到对齐之后,并不能保证每个域之间的类别能够对齐,类别没有对齐有什么影响呢?论文中并没有很好的说明,那就根据我的理解强行解释一波,比如分类器对源域中的一张图片识别出是一个瓶子的概率最大,是一个马克杯的概率次之,在目标域中有瓶子和玻璃杯这两个类别,但是没有马克杯这个类别怎么办,不好用源域辅助目标域判别了呀。同时,在目标域中识别出瓶子的概率最高(与源域一样),识别是玻璃瓶的概率次高(与源域中马克杯类似),那么通过类别对齐,我们想让源域中马克杯这个类别近似看做是目标域中的玻璃杯,并且将瓶子–马克杯这两个源域之间的类别关系(识别出瓶子概率最高,马克杯次之)也映射到目标域中的瓶子–玻璃杯中。另外,网络学习的目的之一是将数据与标签(类别)完成一种映射,在迁移学习中,我们希望能够通过源域与目标域尽可能的相似(域适应),然后通过源域和目标域完成与标签的映射,因为用到的绝大部分数据是来自源域的,但是目标域中标签之间的关系并不一定和源域的相似,就像域适应一样—源域和目标域数据之间并不一定相似,域适应通过边缘对齐让源域和目标域之间的数据尽可能相似,而任务迁移则可以通过类别对齐,将源域中的类别及类别之间关系(各类别的判别概率)也迁移到目标域的任务空间中,文章提出的深度迁移网络就是基于这一点,期望于同时迁移域、任务,来帮助对目标域的任务判别。边缘对齐好说,之前这么多方法都是边缘对齐,那如何类别对齐呢?作者提出了一个叫做"soft label"的东西来帮助目标分类器优化,而这个"soft label"则是根据源域分类器产生的。好了,文中框架的主要工作也是这两个:
- 通过域融合完成域对齐
- 通过soft labels对齐源域和目标域类别
通过域融合完成域对齐
提出的框架如下:
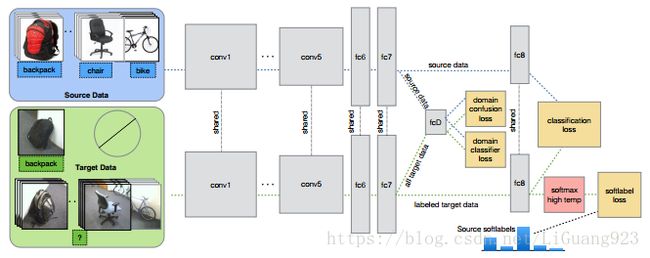
框架是在Alexnet的基础上改动而成,前7层是一个标准的卷积神经网络,而需要做的第一步就是将在源域数据上搭建的卷积网络根据源域有标签数据训练好,这是一个正常的有监督卷积网络训练过程,其损失函数优化如下:
L C ( x , y ; θ r e p r , θ C ) = − ∑ k 1 [ y = k ] l o g p k \mathcal{L}_C(x,y;\theta_{repr},\theta_C)=-\sum_k \mathbb{1} [y=k]logp_k LC(x,y;θrepr,θC)=−k∑1[y=k]logpk
其中 θ r e p r \theta_{repr} θrepr表示的是模型参数,p是分类器中的softmax层的输出: p = s o f t m a x ( θ C T f ( x ; θ r e p r ) ) p=softmax(\theta_C^Tf(x;\theta_{repr})) p=softmax(θCTf(x;θrepr))。
那怎么完成域对齐呢?所基于的思想是啥?----运用生成对抗网络的一种思想,如果一个分类器无法分辨出输入是来自源域还是来自来自目标域的时候,就认为二者已经达到域对齐了。思路已经很清晰了,作者在框架第7层后加了一个域分类器—fcD,用于判别第七层出来的特征表示是属于源域还是目标域,当fcD无法分辨的时候,他们就已经到达了那个传说中的境界----雌雄同体(域对齐,也是域融合,也是域适应),哈哈。还有一个细节就是,fcD是个典型的二分类器,标签就是域标签(例如1表示源域,0表示目标域),分类器的损失函数如下:
L D ( x S , x T , θ r e p r ; θ D ) = − ∑ d 1 [ y D = d ] l o g q d \mathcal{L}_D(x_S,x_T,\theta_{repr};\theta_D)=-\sum_d \mathbb{1} [y_D=d]logq_d LD(xS,xT,θrepr;θD)=−d∑1[yD=d]logqd
其实与上面那个损失函数类似,只不过是把标签换成了域标签。
q和上面的p类似,是域分类器fcD的softmax输出。为了让两个域达到最大融合,提取到更好的域不变(domain invariance)特征以致于最好的域分类器在这些特征上都变现的很差,作者又加了一个损失函数:
L c o n f ( x S , x T , θ D ; θ r e p r ) = − ∑ d 1 D l o g q d \mathcal{L}_{conf}(x_S,x_T,\theta_{D};\theta_{repr})=-\sum_d \frac{1}{D} logq_d Lconf(xS,xT,θD;θrepr)=−d∑D1logqd
啥意思呢?就是在上一步优化了分类器D的基础上,再去优化参数 θ r e p r \theta_{repr} θrepr,这就是一个典型的交叉熵形式。1/D是域概率, q d q_d qd是预测概率。
好了,域对齐OK了,接下来就是作者提出来的用soft label进行任务对齐了。
通过soft labels对齐源域和目标域类别
上面提到soft labels由源域分类器产生,然后通过soft labels优化目标任务空间,而不是像正常的图像标签。那么soft label怎么来呢?上面提到了将源域的类别即类别之间的关系迁移到目标域中,当然是用源域的类别信息来做为soft label最合适不过,文中将soft label定义为源分类器对源域中类别k的样本的softmax结果取均值,如下图所示:
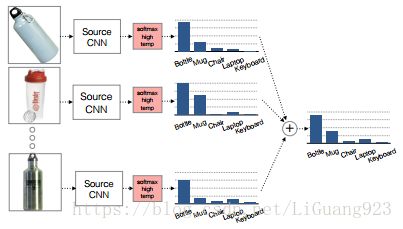
如原图中所示,假设共有5类(Bottle、Mug、Chair、Laptop、keyboard),对模型识别所有属于瓶子类别的样本的softmax值(5个概率)进行平均,像图中得到这个平均值(图中最右边)就是得到的一个soft label(一种关系的衡量,比如在这里是瓶子的概率最高,马克杯的概率次之,其他几种基本不是)。好了,现在soft label也得到了,怎么优化呢?首先,需要给出优化函数,如下:
L s o f t ( x T , y T ; θ r e p r , θ C ) = − ∑ i l i ( y T ) l o g p i \mathcal{L}_{soft}(x_T,y_T;\theta_{repr},\theta_{C})=-\sum_i l_i^{(y_T)} logp_i Lsoft(xT,yT;θrepr,θC)=−i∑li(yT)logpi
其实也是和上面的损失函数类似的,同样是交叉熵形式,通过数据和标签优化特征表示和分类器,其中 l l l表示soft label,因为数据集中目标域也存在部分带标签数据,所以这里和有监督的优化类似,无标签的就用上soft label,为了让类别之间的联系更好的影响到微调,作者在 p i p_i pi中加入了一个权重参数, p i = s o f t m a x ( θ C T f ( x T ; θ r e p r ) / τ ) p_i=softmax(\theta_C^T f(x_T;\theta_{repr})/\tau) pi=softmax(θCTf(xT;θrepr)/τ),其中 τ \tau τ是一个权重参数。
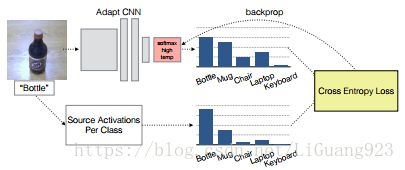
如上图所示,通过源分类器得到soft label,然后使用soft label以及目标域自身的标签求得交叉熵损失,通过后向传播优化目标网络。这也与最上面那个网络框架图中最后一坨对应。然后总结一下所有的损失函数:
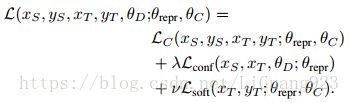
其中 l a m b d a 、 v lambda、v lambda、v是权重参数。和上面一样, θ r e p r \theta_{repr} θrepr表示1-7层的特征参数, θ C \theta_C θC对应的第8层的分类器参数。 θ D \theta_D θD对应fcD域分类器参数。
通过这样,就达到了作者关于域对齐和任务对齐的目的。实验感兴趣的可以另外查看论文。
参考
Hoffman J, Tzeng E, Darrell T, et al. Simultaneous Deep Transfer Across Domains and Tasks[J]. 2015, 30(31):4068-4076.